Дифференциальные уравнения.

1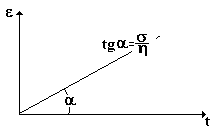.; . При ползучести σ = const. ;; . При t = 0, ε = 0 и С =0..

2. ; . При релаксации: . .; ; . При t = 0, , тогда константа . , , , где - время релаксации.

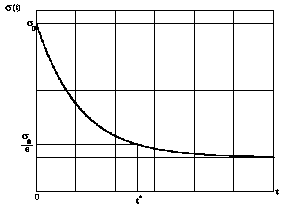
3.;; dt; ; ; = ; || = ; ; ;

; .

4.;; ; ; . При t = 0 ε = . =; . Здесь - время упругого последействия.

5.1). Опишем на языке знаков условие задачи.Т - температура тела в произвольный момент времени t, Т₁ = 35,5⁰ С - температура тела в момент первого наблюдения, Т₂ = 35,0⁰ С - температура тела в момент второго наблюдения, Т₀ = 22⁰ С - постоянная температура окружающей среды, Т_N = 36,7⁰ С - температура тела в момент смерти, τ = 9 часов 30 минут - момент первого наблюдения, t - время, прошедшее с момента наступления смерти, t₁ - время, прошедшее с момента наступления смерти до первого наблюдения, t₂ - время, прошедшее с момента наступления смерти до второго наблюдения,Δt = 1 час - промежуток времени между первым и вторым наблюдением, t₂ = t₁ + Δt, k - коэффициент пропорциональности между скоростью охлаждения и разностью температур тела и окружающей среды.2). Составим знаковую модель в виде математической модели., где знак « - » означает охлаждение. 3). Решим дифференциальное уравнение, разделив переменные.,,,.

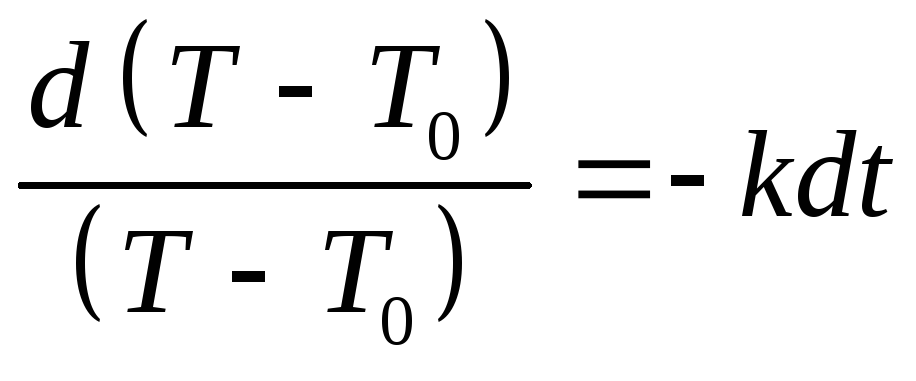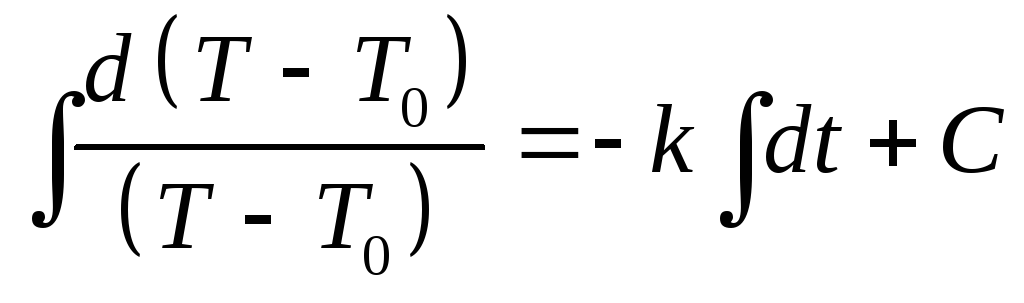4). Получим частное решение уравнения (решим задачу Коши).,

.

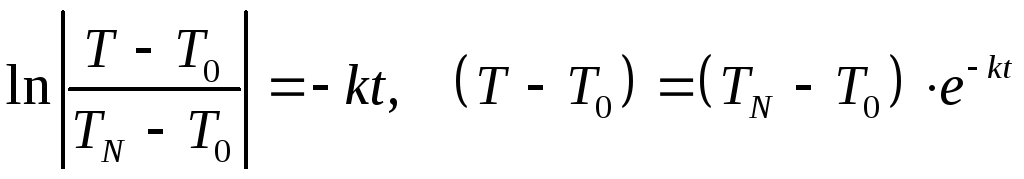Константу скорости охлаждения k находим:

Разделив (1) на (2) получаем константу k:

5). Вычисляем момент наступившей смерти:

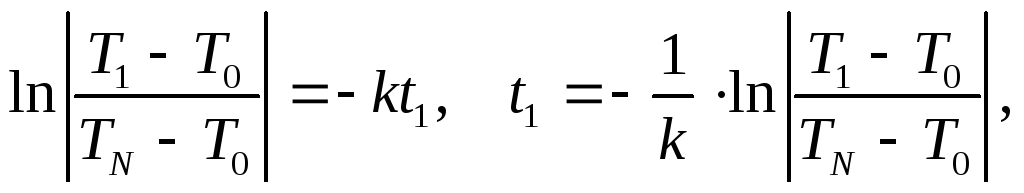
t₁ = 2,26 часа ≈ 2 часа 15 минут

Момент смерти: τ - t₁ = 9 часов 30 минут - 2 часа 15 минут = 7 часов 15 мин по местному времени.

6. ; ; ;.

7.;λ;λ. , где - вероятность безотказной работы.

8.; λ;λ.

9.1).Проанализируем условия стационарного течения по трубке: при стационарном течении вязкой жидкости по трубке объёмная скорость течения (расход) жидкости постоянен во времени. Отсюда следует, что слой жидкости, находящийся на некотором расстоянии от оси трубки должен двигаться с определённой неизменной во времени скоростью, т.е. в трубке должно наблюдаться «телескопическое» течение. Каждый из коаксиальных цилиндрических слоёв должен иметь постоянную скорость.

2). Истолкуем полученный результат с позиций законов динамики: с точки зрения законов динамики описанная ситуация возможна только в случае скомпенсированного действия сил на каждый из тонких коаксиальных слоёв.3). Проиллюстрируем сказанное рисунком.

V = const, F_Т = F_Д

4). Запишем равенство сил, используя понятие напряжение сдвига, реологический закон Ньютона и приняв во внимание, что градиент скорости направлен от стенки трубки к оси: для приосевого цилиндра радиуса rF_Д =,F_Т = откудадля любой жидкости. Для ньютоновской жидкости, поэтому. 5). Решим полученное обыкновенное дифференциальное уравнение с разделяющимися переменными, частное решение получим, приняв во внимание условие на стенке трубкиV = 0 при r =R.

Ответ: откуда

,,,.

10. .Подстановка полученного выражения второй производной висходное уравнение обращает его в тождество.

(t -	(t –
(t -	(t -
(t -	(t -
(t -

11.

12.;. Пусть, тогда дляпорядок дифф.ура окажется ниже на единицу.;

;;;;;;. Полученное общее решение легко идентифицируется с законом движения при прямолинейном равноускоренном движении, который изучался Вами в 8 классе средней школы.проекция ускорения на ось х,- начальная скорость,- начальная координата.

13. См. решение задачи 12.,,Возможны два случая:и. В первом случае проекция ускорения будет положительна, а во втором– отрицательна.

14.См. решение задачи 12,13.

15.См. решение задачи 12,13.

16. ;;;;;;{

17. 1). Уравнение:― обыкновенное дифференциальное уравнение с разделяющимися переменными. 2)..

3). . 4).. 5).;, где. И окончательно:.

18.

19.

20. ..

21. .

22. .

23. .

24. .

25. 1). ЕслиA– наличное количество жителей города в момент времениt, то по условию прирост за времяdtбудетdA=k₁·A·dt, гдеk₁ – коэффициент пропорциональности. Отсюда найдём скорость прироста:

2). Кроме того, население увеличивается за счёт иммиграции, так что скорость прироста населения в целом равна: гдеk₂ – отличный от k₁ коэффициент пропорциональности.

3). Полагая в полученном уравнении: будем иметь:

4). Выберем функцию v таким образом, чтобы выражение в скобках обратилось в нуль, т.е. Из этого уравнения найдёмv: .

5). Из уравнения определяем

Итак,

Из начального условия A(0) =A₀находим:Тогда искомая зависимость числа жителей города от времени выразится формулой:

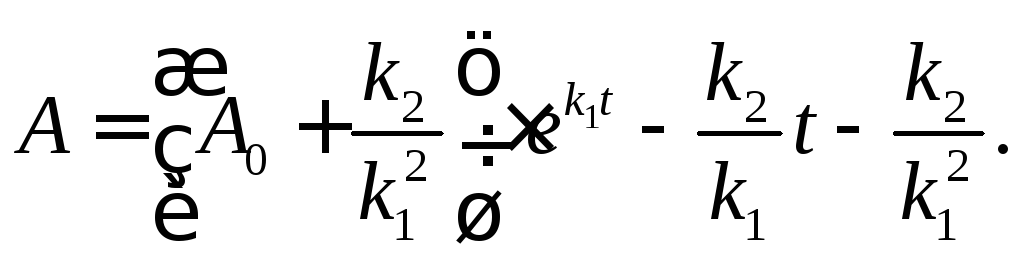
26.1). Уравнение с разделяющимися переменными приведём к уравнению с разделёнными переменными, разделив обе части уравнения на произведение ,:

. 2). Интегрируем полученное уравнение:

.

В нашем случае для упрощения вида общего решения, произвольную постоянную удобнее записать в логарифмическом виде:

.

Тогда общий интеграл (общее решение) уравнения примет вид:

.

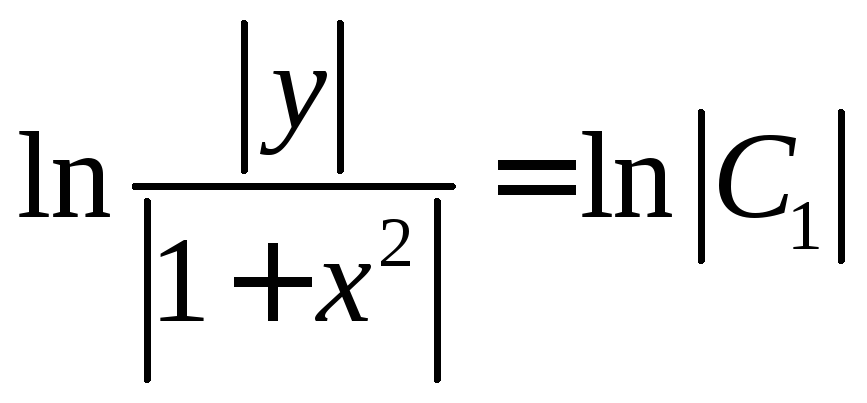3). Выражаем из последнего равенства и получаем общее решение исходного уравнения:

.

4). При делении на предполагалось, что, то есть(для любых). Проверкой убеждаемся, что у = 0 можно получить из формулы общего решения при С₁= 0. Следовательно, у = 0 – частное решение.5). Выделим интегральную кривую, проходящую через точку (1;2). Для этого подставим значения х = 1 и у = 2 в общее решение и определим соответствующее значение С₁:

.

Итак, - искомая интегральная кривая.

27. Обозначим численность населения России в момент времени.

Дифференциальное уравнение исследуемого процесса (скорость «прироста» численности населения) имеет вид , где– коэффициент пропорциональности.

Учитывая, что , имеем- общее решение уравнения.

Согласно условию задачи 145 при. Находим частное решение:

, т.е. С =145, .

Найдём значение коэффициента , зная, что в конце 2000 года, т.е. при1, население России равномлн человек:. Отсюда

, т.е. . Равенствотеперь можно переписать так:

.

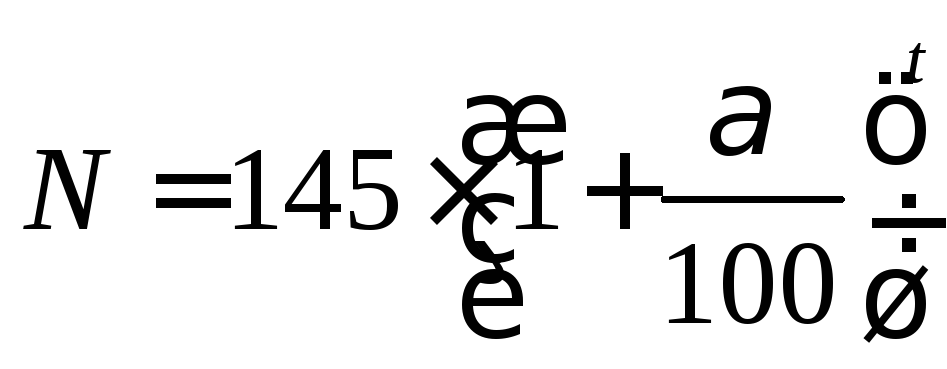Таким образом через 20 лет численность населения составит:

При α = 2%: (млн человек);

при α = -1%: (млн человек).

28. 1). «Функция удовлетворяет уравнению» означает, что при подстановке её и её производных в уравнение, оно обратится в тождество.

2). Найдём первую производную функции поt:

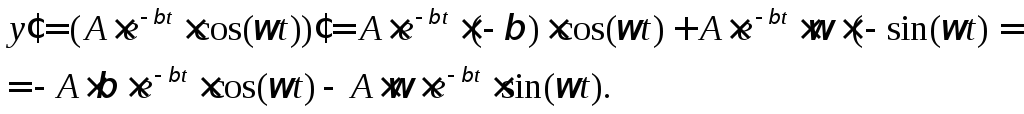
3). Найдём вторую производную функции поt:

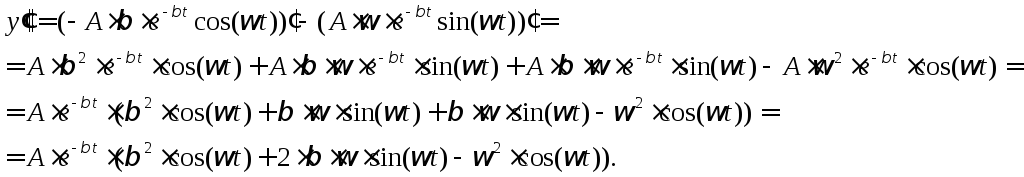4). Получим произведение:

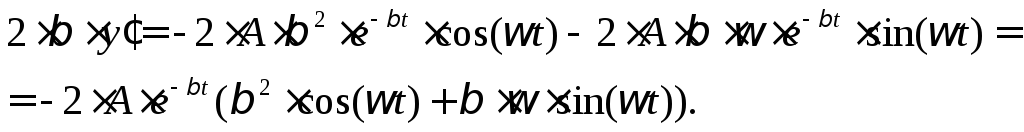
5). Учитывая, что получим:

.

6). Сложив полученные выражения для и приводя подобные, убеждаемся в равенстве нулю полученной суммы:

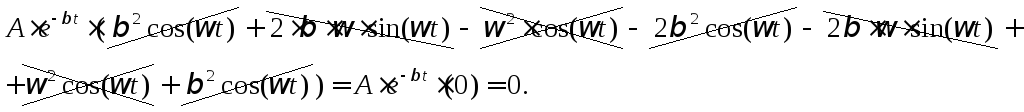
7). Т.о. функция обращает равенство (дифференциальное уравнение)в тождество, т.е. она удовлетворяет дифференциальному уравнению и является одним из решений этого уравнения.

29. По второму закону Ньютона, на движущееся тело действует сила

Дифференциальное уравнение движения в проекциях на вертикальную ось

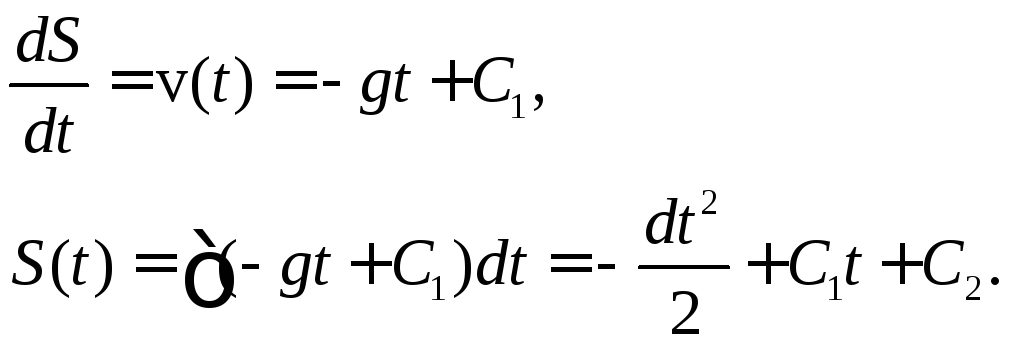
Постоянные интегрирования С₁и С₂найдём из начальных условийv=v₀,S= 0 приt= 0. ИмеемC₁=v₀,C₂= 0. Таким образом, закон движения брошенного вверх тела под действием силы тяжести выражается зависимостями

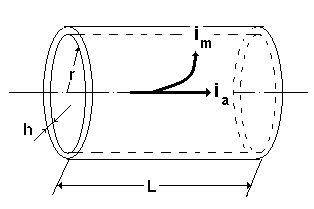
30.Рассмотрим электрические свойства отрезка аксона длинойLи радиусом осевого цилиндраr. Толщину мембраны обозначим черезh.

Пусть -удельное сопротивление аксоплазмы и- удельное сопротивление мембраны.

Электрическое сопротивление отрезка аксона для аксиального тока обозначим как.. Сопротивление единицы длины, так как все единицы числомLсоединены последовательно.

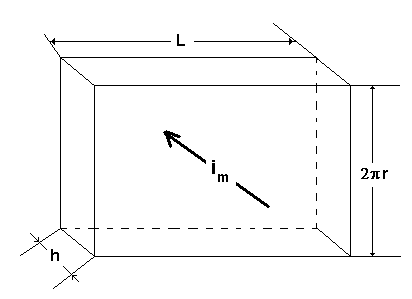
Электрическое сопротивление мембраны отрезка аксона длины Lобозначим, каки найдём , учитывая направление тока через мембрану.

. Учитывая, что сопротивления Lединиц длины для тока через мембрану окажутся соединёнными параллельно, рассчитаем сопротивление, приходящееся на единицу длины..

Обозначим 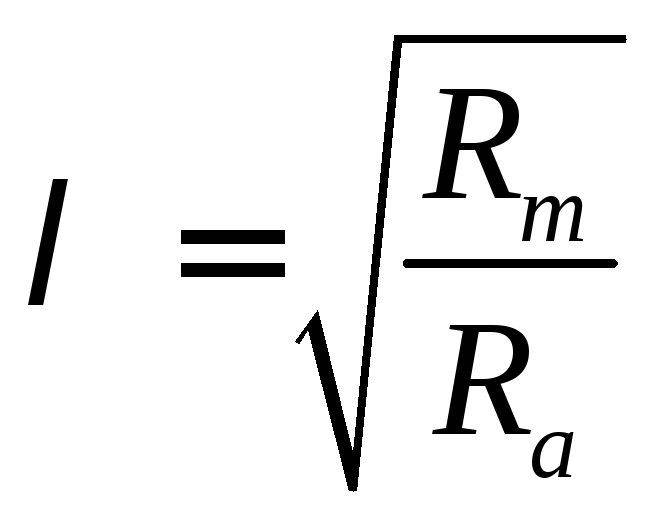и назовём её постоянной длины нервного волокна .

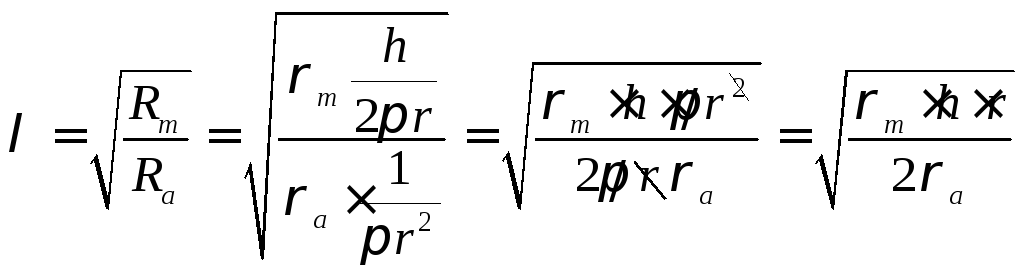
(1).

Рассчитаем теперь аксиальный ток на отрезке нервного волокна , воспользовавшись законом Ома для однородного участка электрической цепи.

.

Силу электрического тока через мембрану можно рассчитать, пойдя двумя путями.

Первый путь основан на законе сохранения электрического заряда. Применительно к рассматриваемому случаю, сила мембранного тока будет равна убыли аксиального тока на участке . То есть:

. (2)

С другой стороны тот же самый мембранный ток должен пройти через мембрану, эквивалентная схема которой представляет параллельно соединённые сопротивление мембраны и ёмкость мембраны.

. (3)

Приравняв левые части выражений (2) и (3), получим дифференциальное уравнение второго порядка в частных производных, которое получило название «кабельное уравнение» или «телеграфное уравнение».

(4)

Из уравнения: можно получить уравнения для двух частных случаев.

В первом случае получается «стационарное телеграфное уравнение», если предположить, что потенциал Vна мембране удерживается постоянным в точке с координатойx= 0. Для этого случая в качестве решения легко получить зависимость потенциала от координатыxдля заданного момента времениt. Эта зависимость имеет вид:, где- постоянная длины. Очевиден физический смысл. Предположив, чтоx=получим:, где- основание натуральных логарифмов. Таким образом, постоянная длиныпредставляет собой расстояние от точки удержания потенциаладо точки, в которой потенциал будет меньше исходного враз. Чем больше значение постоянной длины, тем меньше окажется изменение потенциала с увеличением расстояния от исходной точки.

Второй частный случай получится, если поинтересоваться тем, как изменяется потенциал в одной и той же точки с течением времени. При этом в уравнении (4) и уравнение преобразуется к виду:. Это уравнение легко интегрируется методом разделения переменных.

Обозначив постоянную времени нервного волокна получим:. Из этой зависимости понятен физический смысл постоянной времени. Она представляет из себя время, в течении которого потенциал в данной точке наблюдения уменьшится враз.

Кабельные постоянные инервного волокна играют важную роль в процессах пространственной и временной суммации допороговых электрических сигналов, происходящих на мембранах нервных клеток.

Зависимость постоянной длины от физических характеристик волокна (1) 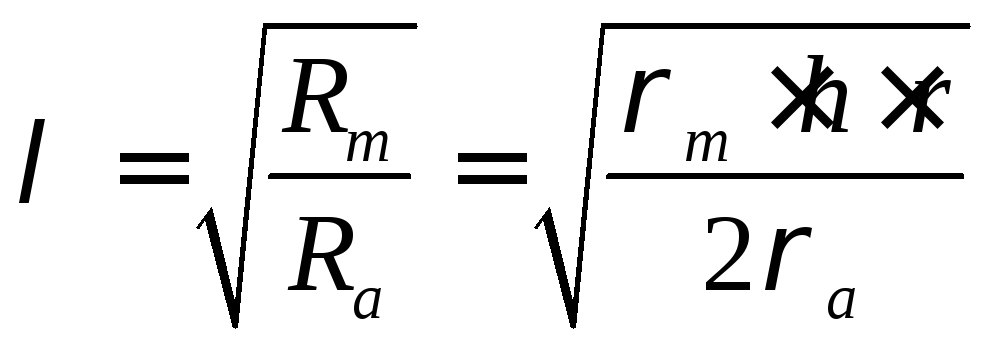указывает на пути возможного увеличения.-удельное сопротивление аксоплазмы и- удельное сопротивление мембраны мало меняются у разных представителей животного мира. Поэтому увеличитьвозможно либо за счёт увеличения радиуса осевого цилиндра нервного волокнаr, что реализовано у гигантского аксона кальмара. Либо за счёт увеличения толщиныh, что реализовано в миелиновом нервном волокне за счёт швановской оболочки.

31.После того, как шарик окажется полностью погружённым в жидкость, на него будут действовать три силы. Сила тяжести, выталкивающая сила Архимедаи сила Стокса. В проекциях на вертикальную ось второй закон Ньютона будет выглядеть с математической точки зрения как обыкновенное дифференциальное уравнение второго порядка:

или.

Это уравнение решается понижением порядка. Обозначив ,каки учитывая:придадим уравнению вид:

Решением полученного уравнения является скорость vкак функция времени –v(t). Получить решение уравнения можно, если разделить переменные и переписать его в дифференциалах.

lnПриняв за начальные условия:, получим, и частное решение:ln. Далее:ln,,. При.