matem_praktikum13

11

х х и т. д.

Теорема (о связи бесконечно малой функции и предела). Если функция f(x)

при х х0 имеет предел, равный числу А, то она может быть представлена в виде f(x)= A + (x), где (x) – бесконечно малая.

Справедливо и обратное утверждение: Если функцию f(x) можно представить в виде суммы числа А и бесконечно малой функции x , то число А является преде-

лом функции f(x) при х х0.

Основные теоремы о пределах

Теорема 1. Предел постоянной равен самой постоянной: lim C C .

x x0

Теорема 2. Предел алгебраической суммы двух функций равен сумме их преде-

лов при условии, что эти пределы существуют:

	lim f1 x f2		x lim	f1 x lim f2 x
	x x0		x x0	x x0
Теорема 3. Предел произведения двух функций равен произведению пределов,
если последние существуют:
		lim f1 x f2	x lim	f1 x lim f2 x
	x x0		x x0	x x0
Следствие 1. Постоянный множитель может быть вынесен за знак преде-
ла: lim C f ( x ) C lim		f ( x )
x x0	x x0
Следствие 2. Предел степени с натуральным показателем равен той же сте-
пени предела:	n		n
	lim f ( x )	lim f ( x ) .
	x x0	x x0

Теорема 4. Предел отношения двух функций равен отношению их пределов, ес-

ли последние существуют, и предел делителя отличен от нуля:

		f1	x			lim f1 x			lim f2 x 0 .
	lim					x x0		, если
		f2	x			lim f2 x
	x x0								x x0
						x x0

Решение задач

П р и м е р 1.1. Вычислить lim 3x2 x 5

x 2

12

Решение. Используя теоремы о пределах, находим:

lim 3x2	x 5 lim 3 lim x lim x lim x lim 5 3 2 2 2 5 9
x 2	x 2	x 2	x 2	x 2	x 2
Часто бывает, что функция y=f(x) при x x0					не определена, но lim f ( x ) суще-
					x x0

ствует. В этом случае для отыскания предела нужно предварительно выполнить пре-

образование функции.

П р и м е р 1.2. Вычислить	lim	x2	6 x 8
			x 2
	x 2

Решение. Применяя непосредственно теоремы о пределах, имеем:

x2

6 x 8

lim ( x2 6 x 8 )

0

lim

x 2

x 2

lim ( x 2 )

0

x 2

x 2

Выражение вида

0

в математике носит название неопределенности вида

0

. В

0

0

этом случае для отыскания предела нужно предварительно преобразовать дробь, раз-

ложив числитель x2 + 6x+8 на множители: x2 + 6x+8 = (x + 2) (x + 4). Квадратный трехчлен ax2+bx+c разлагается на множители ax2+bx+c=a(x – x1) (x – x2), где x1 и x2 –

2

x

b

b2 4ac

.

корни уравнения ax +bx+c которые определяются по формуле:

1,2

2a

Тогда

lim

x2

6 x 8

lim

( x 2 ) ( x 4 )

.

x 2

( x 2 )

x 2

x 4

Сократив числитель и знаменатель на x + 2, получим:

lim	x2 6 x 8	lim x 4 2 .
	x 2
x 2		x 2
П р и м е р 1 . 3. Вычислить lim			x3 2x2		3x 4
				2 2x 1
		x 4x3 3x
Решение. Применив теоремы о пределах, получим неопределенность вида							.

Для ее раскрытия числитель и знаменатель дроби разделим на старшую степень х в

знаменателе, т. е. на х и получим:

13

		3		2				1	2				3					4
	x		2x		3x 4					x
lim							lim							x	2				x	3
					2x 1
x 4x3 3x2							x		3			2					1
								4
										x				x2					x3
Так как неопределенность вида										c		0					, то lim							x3	2x2	3x 4			1	.
																				x 4x3 3x2 2x 1									4

Примерные задания для самостоятельного решения

Вычислить пределы:

1. lim 3x2 x 3 .

x 1

2.	lim		x2	4		.
	x 2 x2 x 6
3.	lim		3x2	1		.
				4x
	x 2x2

	4.	lim	x4		2x2	4		.
			4x3 2x				1
		x
	5.	lim		x2 x 2
					x2 1
		x 1

Контрольные вопросы:

1.Понятие функции.

2.Определение предела функции.

3.Определение бесконечно малой функции.

4.Основные теоремы о пределах.

Задание на дом

1.Лекция по теме «Цели и задачи математики. Производная функции. Диф-

ференциал функции. Производные и дифференциалы высших порядков».

2.Павлушков И.В. и другие стр. 46-70.

14

Лабораторная работа 2. Производная функции. Дифференциал функции.

Производные и дифференциалы высших порядков

Актуальность темы: понятие производной является одним из основных мате-

матических понятий. Производная широко используется при изучении скорости раз-

ных процессов. Дифференциал функции используется при приближенных вычисле-

ниях приращений функции и значений функции.

Цель занятия: закрепить приобретенный в школе навык нахождения произ-

водных функций одной переменной, производных сложных функций, выработать на-

выки нахождения дифференциала функции одной переменной, производных и диф-

ференциалов высших порядков

Целевые задачи:

знать: понятие приращения аргумента и функции, производной функции, ее геометрический и механический смысл, производную сложной функции, основные правила дифференцирования и таблицу производных; понятие дифференциала функции, геометрический и аналитический смысл дифференциала, свойства диффе-

ренциала;

уметь: применять основные правила дифференцирования и таблицу производ-

ных при решении примеров, находить производные сложных функций; находить дифференциалы функций одной переменной, использовать свойства дифференциа-

лов, находить производные и дифференциалы функций одной переменной.

Краткие сведения из теоретического курса

Производная функции

Пусть функция y=f(x) определена на некотором интервале.

Определение. Приращением аргумента называется разность между двумя значениями аргумента х= х - х0.

Разность между двумя значениями функции называется приращением функ-

ции: Δy= Δf = f(x0-x)-f(x0)

Определение. Если функция f (x) определенная на промежутке (a; b), то произ-

водной функции f(x) в точке x0 ( a;b ) называется предел отношения приращения

15

функции f	f ( x0	x ) f ( x0 ) к приращению независимого	переменного
x ( x x x	) при x, стремящемся к нулю lim f .
0		x 0 x
		Производная сложной функции
Теорема (о производной сложной функции): Если функция u g( x )				имеет
производную u ( x ) g ( x ) в точке х, а функция y f ( u ) – производную			yu	f ( u ) в

соответствующей точке и, то сложная функция y f ( g( x )) в данной точке x име-

ет производную yx F ( x ), которая находится по формуле yx			f ( u ) u ( x ).
Механический смысл производной: мгновенная скорость прямолинейного дви-
жения есть производная от пути S по времени t.
Физический смысл производной: если y=f(x) описывает какой-либо физический
процесс, то производная y есть скорость протекания этого процесса.
Геометрический смысл производной: производная
		f x в точке х равна угло-

вому коэффициенту касательной к графику функции y f x в точке, абсцисса кото-

рой равна х.

Таблица основных формул дифференцирования

1.( C )'x 0 .

2.( x )'x 1 .

3. ( un )'	x	n un 1	u'	x	;	( xn )'	x	n xn 1 .

4.( u v w )'x u'x v'x w'x .

5.( u v )'x v u'x u v'x .

( c u )'x c u'x ;

1

u

'

1

u'x .

6.

c

x

c

u '

v u'

x

u v'

x

7.

.

v2

v x

8.

( au )'

x

au u'

x

ln a ;

( ax )'

x

ax ln a .

9.

( eu )'

x

eu u'

x

;

( ex )'

x

ex .

16

10.	(loga u )'x				u'x		;
					u ln a
11.	(lg u )'	x			u'x			u'x	0,4343;
				u ln 10
								u

12.(lnu )'x uu'x ;

13.(sin u )'x cos u u'x ;

14.(cos u )'x sin u u'x ;

15.	( tgu )'x		1			u'x ;
		cos2 u
16.	( ctgu )'x				u'x		;
				sin2 u

	(loga x )'x					1		.
							x ln a
	(lg x )'			1		0,4343 .
		x		x

(ln x )'x 1x .

(sin x )'x cos x .

(cos x )'x sin x .

	( tgx )'x		1			.
		cos2 x
	( ctgx )'x		1				.
				sin2
						x

Дифференциал функции

Дифференциал функции равен произведению производной этой функции на дифференциал аргумента: dy df f ' ( x ) dx .

Аналитический смысл дифференциала функции заключается в том, что диф-

ференциал функции, есть главная часть приращения функции f. Дифференциал функции отличается от приращения функции на бесконечно малую более высокого

порядка малости, чем x. Действительно,	f f ' ( x ) x ( x ) x или
f df ( x ) x .

Свойства дифференциала функции:

1)дифференциал постоянной: dc 0 ;

2)дифференциал суммы. d u v du dv ;

3)дифференциал произведения. d uv udv vdu ;

u				vdu udv
4) дифференциал частного. d					;
				v2
v

5) дифференциал сложной функции. Дифференциал сложной функции (функции от функции) равен произведению производной этой функции по промежуточному ар-

гументу на дифференциал этого промежуточного аргумента(при условии, что обе

		17
функции	дифференцируемы):		где	y f g x ,	и	функции
		df yu du ,
y f u ,	u g x – дифференцируемые функции своего аргумента.
	Геометрический смысл дифференциала функции
Дифференциал функции y=f(x) в точке х равен приращению ординаты каса-
тельной к графику функции в этой точке, когда х получит приращение					х (рис. 2.1).

Рис. 2.1

Равенство y dy f

x x позволяет с большой точностью вычислять при-

ближенно

приращение

любой

дифференцируемой

функции;

формула

для вычисления

приближенных

значений

f x x f x f x x используется

функций.

Производные высших порядков

Производная y

f x

есть также функция от х и называется

f x функции y

производной первого порядка.

Если функция

f

то ее производная называется произ-

x дифференцируема,

водной второго порядка и обозначается

y

или

y

f x . Итак,

y .

Производной n –го порядка или n-ой производной называется производная от

производной (n-1) порядка:

y n y n 1 .Производные порядка выше первого назы-

ваются производными высших порядков.

Механический смысл производной второго порядка

Пусть материальная точка М движется прямолинейно по закону S = f(t). Как уже известно, производная St’ равна скорости точки в данный момент времени:

18

St’= V.

Пусть в момент времени t скорость точки равна V, а в момент t + t – скорость равна V + V, т. е. за промежуток времени t скорость изменилась на величину V.

Отношение V выражает среднее ускорение движения точки за время t. Пре-

t

дел этого отношения при t 0 называется ускорением точки М в данный момент t и

обозначается буквой а: lim	V	a,	Vt a. Итак, вторая производная от пути по
t 0	t

времени есть величина ускорения прямолинейного движения точки, т. е. S a .

Дифференциалы высших порядков

Пусть y=f(x) дифференцируемая функция, а ее аргумент х – независимая пере-

менная. Тогда ее первый дифференциал dy f x dx есть также функция х, можно найти дифференциал этой функции.

Дифференциал от дифференциала функции называется ее вторым дифферен-

циалом (или дифференциалом второго порядка) и обозначается d 2 y : d 2 y d dy .

Дифференциал второго порядка от данной функции равен произведению вто-

рого порядка этой функции на квадрат дифференциала независимой переменной: d 2 y f x dx2 .

Решение задач

П р и м е р 2.1. Найти производную функции f x 3x4 4 x

2x 5 .

4

x

4

x

4

2x 5

3x

4

2x 5

Решение. f x 3x

3 4 x4 1 4 x ln4 2 12x3 4 x ln4 2.

3 x4 4 x ln4 2 0

П р и м е р 2.2. Найти производную функции f x

ln x 4

.

ex

x

x

ln x 4

ln x

e

ln x 4

4 e

Решение. f x

ex 2

ex

1

ex ex ln x 4

ex

1

ln x 4

1

ln x 4

1 x ln x 4x

.

x

x

x

e2 x

e2 x

ex

xex

19

П р и м е р 2.3. Найти производную функции f ( x ) x2

esin x .

Решение.

2

e

sin x

x

2

e

sin x

e

sin x

x

2

f ( x ) x

2x e

sin x

e

sin x

x

2

2x e

sin x

e

sin x

cos x

x

2

e

sin x

2x x

2

cos x .

sin x

П р и м е р 2.4. Найти производную функции: f x 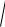tg ex .

																																							1					1
																										f x							tg ex tg								ex		tg ex	2	. Тогда:
				Решение.										Преобразуем							функцию																			2
		x					tg e								1		1	1	e		tg e				1			1	e					1					e
										x										x			x							x
f																tg	2									tg		2
												21																														x
															2										2									cos 2 e x
	1			1										1							ex			1
											cos2 ex ex														ex .
	2				1		ex												2		tg ex cos2
				tg 2
																											f x
				П р и м е р 2.5. Вычислить f 8 , если																												3			x .

													3			31				1		23				1
														x
																x			x
	Решение.										Найдем	f x																.
																			3				3		3		x	2
				1					1
								12 .
f 8			3	8		2
	3
	П р и м е р 2.6. Найти дифференциал функции: f ( x ) ex 2x .
	Решение. На основании свойства 2 дифференциала функции
дифференциала имеем:
	df d ex 2x d ex d 2x exdx 2dx .
	П р и м е р 2.7. Найти дифференциал функции:																	f x ln cos x

Вычислим

и определения

Решение. Функцию можно записать в виде: f x lnu , u cos x . Тогда имеем:

df lnu u du u1 d cos x cos1 x sin x dx cossin xx dx tgxdx

П р и м е р 2.8. Найти вторую производную функции: f x ln 1 2x 1 2x

20

Решение. Преобразуем функцию f x ln 1 2x ln 1 2x ln 1 2x .

1 2x

Найдем первую производную:

ln 1 2x ln 1 2x

f x

1

1

ln 1 2x ln 1 2x

1

2x

1 2x

1 2x

1 2x

2

2

2 1 2x 2 1 2x

4

;

1 2x

1 2x

4x2

1 4x2

1

найдем вторую производную:

4

2 1

2

2

2

f

x f

x

4

1 4x

4 1

4x

1 4x

1 4x2

2

32x

4 1

4x2

8x

.

1 4x2

2

П р и м е р

2.9.

Найти

дифференциал

второго

порядка от функции

f ( x ) sin 2x 3 .

Решение. Найдем дифференциал второго порядка на основании выражения для

вычисления d 2 f :

d	2	f	f	x dx	2			dx	2	. Найдем сначала первую производную:
						sin 2x 3
f							cos 2x				2 cos 2x 3 ; найдем вторую произ-
	x sin 2x 3							3 2x 3

водную: f x 2cos 2x 3 2 sin 2x 3 2x 3 4 sin 2x 3 .

Тогда d 2 f f x dx2 4 sin 2x 3 dx2 .

Примерные задания для самостоятельного решения

Найти производные функций:

1.f ( x ) 2x ln x .

2.f x sin x .

Найти дифференциал функции:

4. f x ln sin x .

3. f ( x ) ln 11 xx .

.

5. f x 1 x3 .