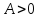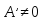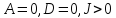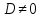- •Министерство сельского хозяйства Российской Федерации
- •Фгбоу впо «Самарская государственная сельскохозяйственная академия»
- •Е. В. Бунтова
- •Математика
- •Введение
- •2.1. Формулы Крамера
- •2.2. Обратная матрица
- •2.3. Матричная запись системы линейных алгебраических уравнений и ее решение методом обратной матрицы
- •2.4. Элементарные преобразования матрицы
- •2.5. Ранг матрицы
- •3.1. Теорема Кронекера-Капелли
- •3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными
- •3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
- •3.4. Однородные системы линейных алгебраических уравнений
- •4.2. Линейные операции над векторами.
- •4.3. Декартова система координат
- •4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме
- •4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме
- •4.6. Применение векторного произведения векторов к решению задач
- •4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме
- •4.8. Применение смешанного произведения векторов к решению задач
- •5.1. Линейное пространство
- •5.3. Разложение вектора по базису. Линейные пространства
- •6.1. Линейные преобразования
- •6.2. Собственные значения и собственные векторы матрицы
- •6.3. Свойства собственных векторов матрицы
- •7.1. Уравнение линии на плоскости. Прямая линия и различные формы ее уравнений на плоскости
- •Свойства прямой в евклидовой геометрии.
- •Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось в точкеи образующая уголс положительным направлением оси
- •Уравнение прямой в отрезках.
- •Нормальное уравнение прямой.
- •7.2. Взаимное расположение двух прямых на плоскости
- •7.3. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых
- •8.1. Каноническое уравнение окружности и ее основные характеристики
- •8.2. Каноническое уравнение эллипса и его характеристики
- •8.3. Каноническое уравнение гиперболы и ее характеристики
- •8.4. Каноническое уравнение параболы и ее характеристики
- •8.5. Исследование кривых второго порядка
- •9.1. Плоскость и ее уравнения
- •9.2. Общее уравнение плоскости и его частные виды
- •9.3. Угол между плоскостями. Условие параллельности и перпендикулярности двух плоскостей
- •9.4. Нормальное уравнение плоскости
- •10.1. Уравнение прямой в пространстве
- •10.2. Условия параллельности и перпендикулярности, прямых в пространстве
- •10.3. Взаимное расположение прямой и плоскости в пространстве
- •11.1. Общая теория поверхностей второго порядка
- •11.2. Классификация поверхностей второго порядка
- •11.3. Расположение поверхностей второго порядка
- •12.1. Определение функции. Функциональная зависимость. Область определения функции и способы ее задания
- •12.2. Графическое изображение функции. Классификации функций
- •12.3. Числовые последовательности и их роль в вычислительных процессах. Ограниченные и неограниченные последовательности
- •12.4. Сходимость числовых последовательностей
- •12.5. Предел функции. Односторонние пределы
- •12.6. Основные теоремы о пределах функции
- •13.1. Первый, второй замечательные пределы и их применение к раскрытию неопределенностей. Бесконечно малые и бесконечно большие функции
- •13.2. Непрерывность функции в точке и на интервале
- •13.3. Классификация точек разрыва функции
- •14.1. Определение производной функции
- •14.2. Геометрический и механический смысл производной
- •14.3. Основные правила дифференцирования
- •14.4. Производная обратной, параметрически заданной функции
- •14.5. Производная показательно-степенной функции.
- •15.1. Теоремы Ферма, Ролля, Лагранжа, Коши
- •15.2. Правило Лопиталя
- •15.3. Дифференциал функции
- •15.4. Применение дифференциала к приближенным вычислениям
- •15.5. Производные и дифференциалы высших порядков
- •16.1. Экстремум функции. Возрастание и убывание функции
- •16.2. Точки перегиба функции и участки выпуклости и вогнутости графика функции
- •16.3. Асимптоты графика функции
- •16.4. Общая схема исследования функции и построение ее графика
- •17.1. Определение функции многих переменных. Область определения функции многих переменных
- •17.2. Частные производные и дифференциалы первого и высших порядков
- •17.3. Теорема о смешанных производных
- •17.4. Производная по направлению
- •18.1. Касательная плоскость и нормаль к поверхности
- •18.2. Необходимое и достаточное условия экстремума функции двух переменных
- •18.3. Условный экстремум функции двух переменных. Наибольшее и наименьшее значения функции на замкнутом множестве
- •18.4. Метод множителей Лагранжа
- •19.1. Первообразная функции
- •19.2. Неопределенный интеграл и его свойства
- •19.3. Таблица основных интегралов
- •19.4. Интегрирование методом замены переменной
- •20.1. Интегрирование по частям
- •20.2. Интегрирование функций, содержащих квадратный трехчлен
- •21.1. Интегрирование элементарных дробей
- •21.2. Интегрирование рациональных дробей
- •22.1. Интегрирование методом замены переменной
- •22.2. Интегрирование по частям
- •22.3. Интегрирование с помощью универсальных подстановок
- •23.1. Линейные и дробно-линейные иррациональности
- •23.2. Квадратичные иррациональности
- •24.1. Задачи, приводящие к понятию определенного интеграла
- •24.2. Определение определенного интеграла
- •24.3. Свойства определенного интеграла. Теорема Коши о существовании определенного интеграла
- •24.4. Формула Ньютона-Лейбница
- •25.1. Геометрические приложения определенного интеграла
- •25.2. Физические приложения определенного интеграла
- •25.3. Методы приближенного вычисления определенного интеграла
- •26.1. Несобственные интегралы с бесконечными пределами интегрирования
- •26.2. Несобственные интегралы от неограниченных функций
- •26.3. Признак сходимости несобственных интегралов (признак сравнения)
- •27.1. Постановка задачи интегрирования функции многих переменных
- •27.2. Двойной интеграл и его свойства
- •27.3. Сведение двойного интеграла к повторному. Изменение порядка интегрирования
- •28.1. Геометрический смысл двойного интеграла
- •28.2. Физические приложения двойного интеграла
- •29.1. Определение криволинейного интеграла
- •29.2. Вычисление криволинейных интегралов первого и второго рода. Условия независимости криволинейного интеграла от пути интегрирования
- •29.3. Формула Грина
- •30.1. Комплексные числа и их изображение на плоскости
- •30.2. Модуль и аргумент комплексного числа
- •30.3. Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами
- •31.1. Задачи, приводящие к составлению и решению дифференциальных уравнений
- •31.2. Дифференциальные уравнения первого порядка. Теорема Коши. Понятие об общем и частном решении дифференциального уравнения. Дифференциальные уравнения с разделяющими переменными.
- •32.1. Линейные дифференциальные уравнения первого порядка. Физические задачи, приводящие к решению дифференциальных уравнений первого порядка
- •32.2. Однородные дифференциальные уравнения.
- •33.1. Дифференциальные уравнения второго порядка,
- •33.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.1. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.2. Особенности интегрирования неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью. Метод вариации произвольной постоянной
- •35.1. Нормальная система дифференциальных уравнений
- •35.2. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами
- •36.1. Особенности составления дифференциальных уравнений в прикладных задачах
- •36.2. Задачи, приводящие к решению дифференциальных уравнений
- •37.1. Определение ряда. Сходимость. Сумма ряда
- •37.2. Необходимый признак сходимости ряда
- •37.3. Достаточные признаки сходимости ряда
- •38.1. Достаточный признак сходимости знакочередующихся рядов
- •38.2. Абсолютная и условная сходимость знакопеременных рядов
- •39.1. Функциональные ряды
- •39.2. Степенные ряды
- •39.3. Теорема Абеля
- •40.1. Разложение некоторых элементарных функций в ряды Тейлора, Маклорена
- •40.2. Приложение рядов к приближенным вычислениям
- •41.1. Периодические функции
- •41.2. Определение ряда Фурье
- •41.3. Ряды Фурье четных и нечетных периодических функций с произвольным периодом
- •42.1. Множества
- •42.2. Подмножество
- •42.3. Операции над множествами
- •Свойства операций:
- •43.1. Общие понятия теории графов
- •43.2. Теорема Эйлера. Операции над графами
- •43.3. Способы задания графов
- •43.4. Комбинаторика как наука
- •43.5. Сочетания. Размещения. Перестановки
- •44.1. Развитие теории вероятностей как науки
- •44.2. Виды случайных событий
- •44.3. Классическое определение вероятности
- •44.4. Относительная частота
- •44.5. Теорема сложения вероятностей для несовместных событий. Противоположные события
- •44.6. Условная вероятность. Теорема умножения вероятностей
- •44.7. Теорема сложения вероятностей для совместных событий
- •44.8. Формула полной вероятности. Формулы Байеса
- •45.1. Формула Бернулли
- •45.2. Наивероятнейшее число наступлений событий
- •45.3. Локальная теорема Лапласа. Интегральная теорема Лапласа
- •45.4. Вероятность отклонения частоты от постоянной вероятности в независимых событий. Асимптотическая формула Пуассона
- •46.1. Дискретные и непрерывные случайные величины
- •46.2. Формы задания законов распределения случайных величин: ряд распределения, функция распределения, плотность распределения
- •46.3. Свойства функции распределения и функции плотности распределения вероятности появления случайной величины
- •46.4. Вероятность попадания случайной величины на заданный интервал
- •46.5. Числовые характеристики случайной величины.
- •47.1. Закон распределения дискретной случайной величины. Биномиальное распределение дискретной случайной величины
- •47.2. Распределение Пуассона дискретной случайной величины. Простейший поток событий
- •47.3. Закон распределения непрерывной случайной величины. Равномерный закон распределения непрерывной случайной величины
- •47.4. Показательный закон распределения
- •47.5. Нормальный закон распределения непрерывной случайной величины
- •47.6. Вычисление вероятности заданного отклонения. Правило трех сигм
- •48.1. Закон больших чисел и его практическое значение
- •48.2. Центральная предельная теорема Ляпунова
- •48.3. Применение закона больших чисел и центральной предельной теоремы
- •49.1. Генеральная и выборочная совокупности
- •49.2. Статистическое распределение выборки
- •49.3. Эмпирическая функция распределения
- •49.4. Полигон и гистограмма
- •50.1. Определение статистических оценок параметров распределения
- •50.2. Виды статистических оценок параметров распределения
- •50.3.Надежность статистических оценок параметров распределения.
- •51.1. Статистическая гипотеза
- •51.2. Статистический критерий
- •51.3. Критерий согласия Пирсона
- •51.4. Критерий Колмогорова
- •51.5. Критерий проверки гипотезы о равенстве дисперсий
- •51.6. Критерий сравнения двух выборочных средних
- •51.7. Критерий Вилкоксона проверки гипотезы об однородности двух выборок
- •52.1. Однофакторный дисперсионный анализ
- •52.2. Двухфакторный дисперсионный анализ
- •53.1. Корреляционная зависимость
- •53.2. Линейная парная регрессия
- •53.3. Оценка значимости параметров связи
- •54.1. Понятие о нелинейной регрессии
- •54.2. Корреляционное отношение
- •54.3. Ранговая корреляция
- •Задания для практических занятий по материалу лекций
- •Словарь терминов и определений
- •Алфавитно-предметный указатель
- •Рекомендуемая литература
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера-Снедекора
- •Критические точки критерия Вилкоксона
- •Оглавление
- •Бунтова Елена Вячеславовна математика
- •446442, Самарская обл., пгт. Усть-Кинельский, ул. Учебная, 2
- •443068, Г. Самара, ул. Песчаная, 1
10.3. Взаимное расположение прямой и плоскости в пространстве
Плоскость,
проходящая
через точку
 и через прямую
и через прямую


не
проходящую через
 представляется
уравнением
представляется
уравнением

Рассмотрим
пример. Плоскость,
проходящая через точку
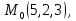 и прямую
и прямую

представляется уравнением

т.е.

Плоскость,
проходящая через точку
 и параллельная данным прямым
и параллельная данным прямым
 и
и
 представляется уравнением
представляется уравнением

где
 направляющие коэффициенты данных
прямых.
направляющие коэффициенты данных
прямых.
Пусть
 и
и – непараллельные прямые. Тогдаплоскость,
проходящая через прямую
– непараллельные прямые. Тогдаплоскость,
проходящая через прямую
 и
параллельная прямой
и
параллельная прямой представляется
уравнением
представляется
уравнением

где
 координаты
точки
координаты
точки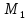 прямой
прямой
Условие параллельности прямой
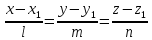
и плоскости


Условие перпендикулярности прямой

и плоскости


Контрольные вопросы
1. Записать уравнения прямой в пространстве: как пересечение плоскостей; каноническое уравнение прямой, проходящей через две заданные точки. Какой смысл имеют коэффициенты этих уравнений?
2. Как найти угол между прямой и плоскостью?
3. Как найти длину перпендикуляра, опущенного на прямую?
Лекция №11. Поверхности второго порядка
11.1. Общая теория поверхностей второго порядка.
11.2. Классификация поверхностей второго порядка.
11.3. Расположение поверхностей второго порядка.
11.1. Общая теория поверхностей второго порядка
Поверхности
второго порядка определяются уравнениями
второй степени относительно декартовых
прямоугольных координат. Общее уравнение
второй степени относительно переменных
 имеет вид
имеет вид


где

Инвариантами поверхностей второго порядка называются числовые функции, составленные из коэффициентов уравнений, сохраняющие постоянные значения при аффинных преобразованиях системы координат.


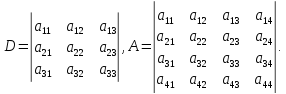
Данные инварианты определят свойства поверхности, не зависящие от ее положения в пространстве.
Аффинным
преобразованием пространства
называется взаимно–однозначное
преобразование системы координат, при
котором точке
 ,
заданной относительно общей декартовой
системы координат, ставится в соответствие
точка
,
заданной относительно общей декартовой
системы координат, ставится в соответствие
точка координаты
которой через координаты точки
координаты
которой через координаты точки выражаются линейными соотношениями
выражаются линейными соотношениями

Данные соотношения обладают свойством взаимной однозначности, если определитель системы уравнений является нетривиальным, т.е.

11.2. Классификация поверхностей второго порядка
Все поверхности второго порядка делятся на 17 аффинных сортов. Необходимые и достаточные признаки каждого из них можно свести в таблицу, основанную на их инвариантах.
Таблица 2
|
Виды поверхностей |
Невырожденные поверхности
|
Невырожденные поверхности
|
Вырожденные поверхности
|
|
Центральные поверхности
|
Мнимый эллипсоид
|
Эллипсоид |
Точка (действительная вершина мнимого конуса) |
|
Центральные поверхности
|
Однополостной гиперболоид
|
Двуполостной гиперболоид |
Действительный конус |
|
Нецентральные поверхности
|
Гиперболический параболоид |
Эллиптический параболоид |
Цилиндры
Пары плоскостей
|
|
_ |
Цилиндры
|
Пары плоскостей
|
– |
|
Виды поверхностей |
Невырожденные поверхности
|
Невырожденные поверхности
|
Вырожденные поверхности
|
|
|
Мнимый эллиптический цилиндр, если
|
Пара мнимых плоскостей,пересекающихся по действительной прямой |
– |
|
|
Действительный эллиптический цилиндр, если
|
Пара мнимых плоскостей, пересекающихся по действительной прямой |
– |
|
|
Гиперболический цилиндр |
Пара действительных пересекающихся плоскостей |
– |
|
|
Параболический цилиндр |
Пара мнимых параллельных плоскостей, если
|
Пара действительных совпадающих плоскостей |
|
|
Параболический цилиндр |
Пара действительных параллельных плоскостей, если
|
Пара действительных совпадающих плоскостей |
В
этой таблице
 являются инвариантами относительно
поворота осей и определятся следующим
образом
являются инвариантами относительно
поворота осей и определятся следующим
образом


Любые две поверхности, принадлежащие к разным классам, никаким аффинным преобразованием не могут быть переведены друг в друга.
Мнимый эллипсоид, мнимый эллиптический цилиндр и две мнимые параллельные плоскости не содержат ни одной точки, значит аффинно не могут быть преобразованы ни в одну из поверхностей остальных аффинных сортов.
Две пересекающиеся плоскости и две совпадающие плоскости отличаются от поверхностей остальных аффинных сортов как единственные, состоящие из плоскостей. Эти свойства сохраняются при любом аффинном преобразовании.
Среди поверхностей остальных аффинных сортов эллипсоид, двуполостной гиперболоид и эллиптический параболоид отличаются от поверхностей других аффинных сортов тем, что не содержат прямолинейных образующих. Эллипсоид поверхность ограниченная, а двуполостной гиперболоид и эллиптический параболоид – поверхности неограниченные. Двуполостной гиперболоид состоит из двух кусков, а эллиптический параболоид из одного куска. Это различие сохранится при любом аффинном преобразовании.
Среди остающихся поверхностей конус отличается от поверхностей остальных сортов тем, что представляет собой поверхность, образованную прямыми, проходящими через одну точку и не лежащими в одной плоскости. Эллиптический, гиперболический и параболический цилиндры отличаются тем, что образованы параллельными прямыми. Сечения их плоскостями, не параллельными образующим, будут соответственно эллипсами, гиперболами и параболами. Указанные различия поверхностей сохраняются при любых аффинных преобразованиях.
Однополостной гиперболоид от гиперболического параболоида отличается тем, что первая поверхность имеет центр симметрии, а вторая не имеет центра симметрии. Указанные различия поверхностей также сохраняются при любых аффинных преобразованиях.
Все поверхности второго порядка можно разбить на пять групп по признаку места центров. Необходимые и достаточные признаки принадлежности поверхностей к одной из групп можно свети в таблицу (табл. 3).
Таблица 3
|
Номер группы |
Признак группы |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Определение характера места центров симметрии важно знать для приведения уравнения к каноническому виду. Общее уравнение поверхности может быть приведено к одному из пяти видов
1)
2)
3)
4)

5)

Чтобы
привести уравнение поверхности к одному
из вышеперечисленных видов, необходимо
найти
 из
уравнения
из
уравнения

Рассмотрим пример. Уравнение поверхности привести к каноническому виду и определить координаты центра поверхности

Находим


Так
как
 то
данное уравнение выражает однополостной
гиперболоид.
то
данное уравнение выражает однополостной
гиперболоид.
Характеристическое уравнение

имеет
корни

Каноническое уравнение

или

Координаты центра поверхности найдем, решая систему


Центр