
- •Министерство образования и науки
- •Введение
- •1. Основы теории инженерного эксперимента
- •1.1. Эксперимент как объект исследования
- •1.2. Основы теории обработки результатов эксперимента
- •Анализ случайных ошибок
- •Анализ и исключение грубых ошибок
- •Матрицы корреляционных моментов и корреляционных коэффициентов
- •Вероятностный способ расчета потерь энергии
- •Регрессионный анализ
- •Полный факторный эксперимент (пфэ)
- •Дробный факторный эксперимент (дфэ)
- •Свойства матриц пфэ и дфэ
- •Проведение эксперимента и обработка результатов опыта
- •Проверка адекватности математического описания
- •Обработка результатов эксперимента при неравномерном дублировании опытов
- •Обработка результатов экспериментов при отсутствии дублирования опытов
- •Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
- •Экспериментальные планы, рекомендуемые для решения электроэнергетических задач
- •Литература
Вероятностный способ расчета потерь энергии
Решение задачи для реальных сетей переменного тока связано с громоздкими преобразованиями, поэтому рассмотрим упрощенную задачу: расчет потерь в сети постоянного тока.
Потеря мощности
линии, соединяющей узлы i
и j
сети постоянного тока, имеющей проводимость
![]() ,
определяется по формуле:
,
определяется по формуле:
![]() . (37)
. (37)
Для определения потерь мощности во всей сети необходимо суммировать потери по всем линиям:
![]() .(38)
.(38)
Выражение потерь
мощности в окрестности точки математических
ожиданий напряжений
![]() представим рядом Тейлора, в котором
учтем члены первого и второго порядков
малости:
представим рядом Тейлора, в котором
учтем члены первого и второго порядков
малости:
 .(39)
.(39)
Чтобы от потерь
мощности ![]() перейти к потерям энергии за интервал
Т
(
перейти к потерям энергии за интервал
Т
(![]() ),
необходимо проинтегрировать формулу
(39), что дает результат:
),
необходимо проинтегрировать формулу
(39), что дает результат:
 ,(40)
,(40)
где  - это корреляционный момент напряжений
узлов i,
j.
В формуле выделим две составляющие:
- это корреляционный момент напряжений
узлов i,
j.
В формуле выделим две составляющие:
![]() - определяется
математическим ожиданием (постоянная
часть потерь энергии);
- определяется
математическим ожиданием (постоянная
часть потерь энергии);
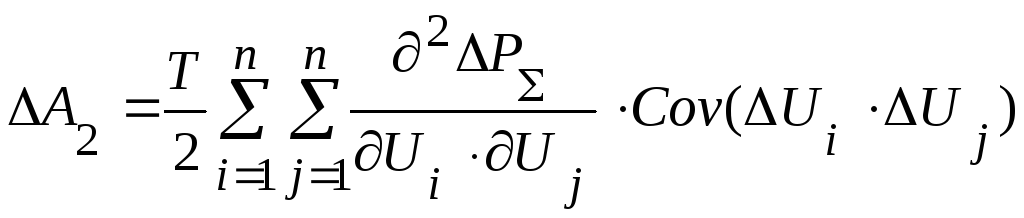 - определяется
колебаниями мощности в окрестности MU
- дисперсионная составляющая.
- определяется
колебаниями мощности в окрестности MU
- дисперсионная составляющая.
Из (40) следует, что
![]()
После ряда преобразований простейшая формула для определения потерь энергии принимает вид:
 (41)
(41)
Формула (41) обычно используется в численных расчетах потерь мощности и энергии.
Пример №4.
Определить ![]() для части электрической системы (рис.
1.4) по формуле (41),
для части электрической системы (рис.
1.4) по формуле (41),
где ![]() - потери мощности, соответствующие
режиму математических ожиданий нагрузок
(
- потери мощности, соответствующие
режиму математических ожиданий нагрузок
(![]() );
);
Т - временной интервал потерь энергии (Т=24 ч);
![]() - элементы матриц
корреляционных моментов мощностей и
сопротивлений.
- элементы матриц
корреляционных моментов мощностей и
сопротивлений.
Последовательность расчета.
1. Находим потери
мощности, соответствующие режиму
математических ожиданий
![]() .
Результаты расчета режима математических
ожиданий приведены на рис. 1.6.
.
Результаты расчета режима математических
ожиданий приведены на рис. 1.6.

Отдельные формулы расчета.
![]() ;
;
![]() ;
;
![]() .
.
Решая эту систему уравнений получаем: MU1 = 201,7 кВ; MU2 = 200,43 кВ; MU3 = 204,53 кВ.
 МВт,
МВт,
Аналогично: ![]()
![]()
Для расчета ![]() прежде находим обратную матрицу
проводимостей, равную Y-1
= Z. Эта операция выполняется методом
единичных токов и приводит к следующему
результату:
прежде находим обратную матрицу
проводимостей, равную Y-1
= Z. Эта операция выполняется методом
единичных токов и приводит к следующему
результату:

Элементы матрицы
![]() найдены в примере №2. Подставляя их
значения в (41) получаем численное
выражение для дисперсионной
составляющей потерь
найдены в примере №2. Подставляя их
значения в (41) получаем численное
выражение для дисперсионной
составляющей потерь ![]() :
:

Отсюда:
![]() МВт.
ч.
МВт.
ч.
Этот расчет дает значительно меньшую погрешность, чем расчет потерь по существующему методу максимального режима и времени максимальных потерь .
Регрессионный анализ
Регрессионный
анализ предназначен для нахождения по
результатам эксперимента связи выходной
характеристики объекта у
с факторами, которые влияют на эту
характеристику
![]() (х1,
х2...хn).
Объект является регрессионным, если
зависимость между выходным параметром
Y
и входными переменными
(х1,
х2...хn).
Объект является регрессионным, если
зависимость между выходным параметром
Y
и входными переменными
![]() =
(х1,
х2...хn),
доступными для наблюдения, имеет вид:
=
(х1,
х2...хn),
доступными для наблюдения, имеет вид:
![]()
где - наблюдаемый в нормальных условиях случайный сигнал,
![]() - априори неизвестный
функционал, определяющий зависимость
Y
от
- априори неизвестный
функционал, определяющий зависимость
Y
от
![]() .
.
Величина у
является случайной, имеет нормальное
распределение с математическим ожиданием
MY,
изменяющемся при изменении факторов
![]() ,
и постоянную дисперсию
,
и постоянную дисперсию![]() ,
т.е. не зависящую от
,
т.е. не зависящую от![]() .
.
Выражение MY
= ![]() называется уравнением регрессии
математического ожидания случайной
величины у
по неслучайным величинам х1,
х2...хn.
называется уравнением регрессии
математического ожидания случайной
величины у
по неслучайным величинам х1,
х2...хn.
В основе регрессионного анализа лежат следующие предположения:
1) при каждом сочетании значений х1, х2...хк величина у имеет нормальное распределение;
2) дисперсия
![]() - постоянная;
- постоянная;
3) тип функционала
MY
= ![]() известен;
известен;
4) независимые переменные х1, х2...хк измеряются с пренебрежительно малыми ошибками по сравнению с ошибкой в определении у;
5) переменные х1, х2...хк линейно независимы.
При обработке
результатов многофакторного эксперимента
функцию MY
= ![]() обычно представляют в виде полинома
первой или второй степени:
обычно представляют в виде полинома
первой или второй степени:
![]() (42)
(42)
![]() (43)
(43)
где 0, 1, 2 - коэффициенты уравнений регрессии.
Задачи регрессионного анализа:
1) проверка
однородности оценок дисперсии
![]()
2) нахождение оценок b0, b1, b2,..., bkk параметров 0, 1, 2,..., kk;
3) определение доверительных интервалов для 0, 1, 2,..., kk и проверка значимых оценок;
4) проверка гипотезы адекватности.
Регрессионный анализ линейного уравнения выполняется по следующему алгоритму:
1. Составляют Х-матрицу условий опытов и Y-матрицу наблюдений.
2. Строят матрицу Х*, транспонированную к Х-матрице.
3. Вычисляют матрицу произведения Х*Х.
4. Находят матрицу (Х*Х)-1, обратную матрице Х*Х.
5. Вычисляют матрицу произведений Х*Y.
6. Определяют коэффициенты уравнения регрессии.
7. Находят Сov{bibj} и оценки S2{bi} дисперсий 2{bi}.
8. Вычисляют дисперсию адекватности модели S2ад и проверяют гипотезу адекватности уравнения регрессии.
Оценку уравнения регрессии (42) запишем в виде:
![]() (44)
(44)
где у - выборочная оценка MY,
х0 - фиктивная переменная, равная х0=1.
Для решения поставленной задачи число опытов N должно быть равно или больше числа коэффициентов уравнения регрессии, т.е. N (k+1), где (k+1) - число коэффициентов bi.
Оценки b0, b1, b2,..., bk параметров 0, 1, 2,..., k уравнения (42) определяют по МНК по результатам N опытов.
Регрессионный анализ уравнения регрессии в виде полинома второго порядка (43) при 2х факторах выполняют следующим образом.
Оценка уравнения регрессии (43) имеет вид:
![]() (45)
(45)
Введем обозначения:
![]() Тогда уравнение (45) примет вид линейного
уравнения:
Тогда уравнение (45) примет вид линейного
уравнения:
![]()
Решение уравнения аналогично предыдущему.
