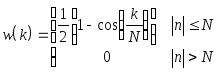6. Расчет нерекурсивных цифровых фильтров.

Определение временной последовательности h(n) по известной передаточной функции и составляет понятие расчета нерекурсивных фильтров. Согласно (6) , h(n) и являются парой преобразования Фурье в дискретном времени. Поскольку вследствие временной дискретизации является периодической функцией частоты с периодом, равным частотному интервалу Найквиста , то преобразование (6) можно рассматривать как разложение в ряд Фурье, а h(k) - коэффициенты Фурье этого разложения. Таким образом, расчет рекурсивных фильтров фактически сводится к разложению передаточной функции в ряд Фурье.

Рассчитаем для примера вышеупомянутый низкополосной фильтр, т.е. фильтра, пропускающего без изменения интервал частот от 0 до частоты, называемой частотой среза , которая не должна превышать половину частоты Найквиста, и подавляющего все остальные частоты.

Для удобства расчета, перенормируем ось частот ,приняв половину частоты Найквиста за единицу.

(25a).

При этом пределы изменения частота среза будут .

Таким образом, передаточная функция такого фильтра имеет вид прямоугольного импульса , периодически продолженного за пределами интервала Найквиста. Разложение в комплексный ряд Фурье в частотной области имеет вид:

(26)

Соответственно, выражения для коэффициентов следующие:

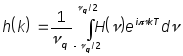(27).

Вычисляя по этой формуле коэффициенты Фурье, подставив получим следующее разложение нашей передаточной функции:

(28).

Учитывая тот факт, что , получим выражение для идеальной передаточной функции низкочастотного фильтра:

(29).

Чтобы преобразовать низкочастотный фильтр в высокочастотный , необходимо вычислить только x(n)-y(n) в качестве нового фильтра. Такой фильтр , наоборот, будет пропускать частоты выше и подавлять ниже частоты среза. Комбинируя низкочастотные фильтры, можно построить полоснопропускающие или полоснозапирающие фильтры.

Так , чтобы построить высокочастотный фильтр, т.е. фильтр, пропускающий полосу и подавляющий полосу , необходимо взять x(n)-y(n) в качестве нового фильтра.

Идеальная передаточная функция полосового фильтра получается комбинированием двух полоснопропускающих фильтров.

(32).

Для практических целей всегда приходится ограничивать формируемый ряд Фурье N членами разложения. Как известно(см.гл.2), усечение ряда Фурье приводит к эффекту Гиббса: осцилляциям вблизи точек разрыва в графике суммы усеченного ряда Фурье разрывной функции. Поскольку этот эффект будет вносить искажения в передаточную функцию фильтра, то требуется найти способ борьбы с этим эффектом. Кроме того, усечение ряда Фурье приводит еще к одному фактору, который надо учитывать при построении цифровых фильтров - это обязательное наличие между полосой пропускания и полосой запирания фильтра так называемой переходной полосы.

Чтобы показать способы влияния на величину переходной полосы, а также устранения эффекта Гиббса, разберемся более детально в причине их появления.

Пусть реальная передаточная функция получается простым усечением соответствующего ряда Фурье. Это усечение можно рассматривать как умножение коэффициентов ряда на множители, равные единице когда индекс по модулю не превосходит N. Таким образом приходим к понятию естественного временного окна.

(32)

Где

(33)

Таким образом, реальную передаточную функцию, полученную обрезанием ряда Фурье, можно представить как свертку идеальной передаточной функции с образом Фурье естественного прямоугольного окна (33).

Т.е. реальная передаточная функция , полученная из идеальной простым усечением, связана с ней следующим образом:

(34).

Чтобы геометрически рассмотреть процесс такой свертки, прежде

оценим ширину центрального лепестка спектрального окна.

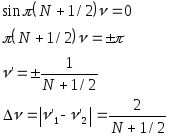
Теперь покажем, что усечение ряда Фурье передаточной функции приводит не только к осцилляциям, но и непременно к существованию некоторой переходной полосы от полосы пропускания к полосе непропускания.

Представим себе геометрически свертку прямоугольной функции (9) с окном (33).

Будем изменять частоту , начиная от некоторого . Так как прямоугольная функция при таких частотах пересекается только с осциллирующим хвостом синусоиды, то значения свертки для таких частот равно нулю. Как только , т.е. главный лепесток (33) войдет в прямоугольный импульс, значение свертки (34) при дальнейшем увеличении частоты начнет расти. При половина главного лепестка войдет в прямоугольный импульс . Значение свертки будет расти до значения частоты , а далее, т. к. значения окна приобретают осциллирующий характер, значения реальной передаточной функции сначала начнет падать, далее снова расти и т.д., повторяя осциллирующий характер хвоста окна на фоне некоторого плато. При дальнейшем увеличении частоты мы в конце концов подойдем к правому краю рассматриваемого фильтра и аналогичным образом сформируется положительно-частотный фронт передаточной функции. Таким образом, в силу конечности используемых на практике фильтров между полосой подавления и полосой пропускания всегда имеется переходная полоса, ширина которой равна ~1/N. Таким образом, чтобы уменьшить переходную полосу, нужно учитывать как можно больше членов разложения передаточной функции в ряд Фурье. На практике ,так как мы хотим иметь как можно меньше членов в разложении и одновременно иметь хорошие характеристики фильтра, необходимо прибегать к некоторому разумному компромиссу. Поэтому при расчете фильтров обычно ширина переходной полосы задается как параметр, который можно реализовать соответствующим выбором порядка фильтра.

Естественной помехой вследствие усечения ряда будем не только переходная полоса, по эффект Гиббса, который приводит к пульсациям передаточной функции. Из теории ряда Фурье нам известно, что такая неравномерная сходимость может быть уменьшена за счет менее резкого усечения ряда Фурье. Если вместо естественного прямоугольного окна использовать окно, постепенно сходящее к нулю с каждой стороны, то можно достичь сглаживания этих колебаний, правда за счет увеличения ширины переходной полосы.

Возьмем ,к примеру, вместо прямоугольного окна треугольное, которое называется окном Бартлетта.

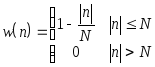
Как известно треугольный импульс можно представить как свертку двух прямоугольных импульсов вдвое меньшей ширины.

Поэтому спектральный вид такого окна можно найти как произведение образов Фурье двух одинаковых прямоугольных окон (33), но с шириной N/2. Кроме того, чтобы максимум треугольного импульса был нормирован на единицу, нужно умножить свертку и ее преобразование на множитель 1/(N/2). Таким образом, окно Бартлетта в частотной области имеет вид

(36).

Сравним это окно с , что главный максимум этого окна равен N/2, в то время как прямоугольного окна N. Ширина центрального лепестка равна 2/N, ширина боковых лепестков 1/N ,что в два раза больше соответствующих расстояний для прямоугольного окна. Отношение главного максимума к первому оказывается на порядок большим, чем для прямоугольного . В результате применения треугольного окна получим, что амплитуда пульсаций в полосе пропускания и в полосе запирания оказывается на порядок ниже, чем для прямоугольного окна, но зато переходная полоса оказывается в два раза шире.

Таким образом мы опять должны выбирать некоторый компромиссный вариант, чтобы обеспечить требуемую ширину переходной полосы и , одновременно, чтобы колебания в полосе пропускания и в полосе запирания не превышали заданного значения.

Еще на порядок лучшего сглаживания можно добиться применением окна Хеннинга: