9.23 . 9.24.

9.25 . 9.26.

9.27 . 9.28.

9.29 . 9.30. 9.31. 9.32.

9.33 . 9.34.

9.35. 9.36.

Уравнение вида приводится к однородному уравнению или уравнению с разделяющимися переменными.

Пусть , тогда:

1) если , то подстановкой, гдеи- новые переменные,и- некоторые числа, определяемые из системы уравнений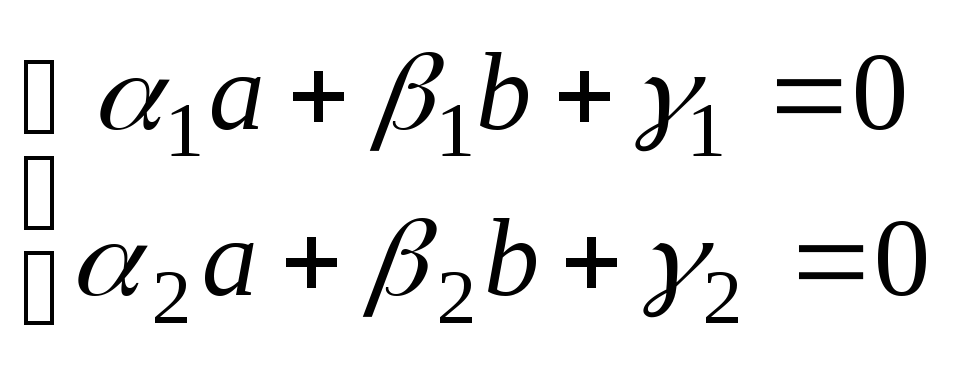, исходное уравнение приводится к однородному ДУ относительно новых переменныхи;

2) если , то подстановкойисходное уравнение приводится к уравнению с разделяющимися переменными.

В задачах 9. 37-9.40 найти общие решения уравнений:

9.37 . 9.38.

9.39.

9.40 .

В задачах 9.41-9.46 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:

9.41 ,.

9.42 ,.

9.43 ,. 9.44,.

9.45 ,.

9.46 ,.

Уравнение вида называетсялинейным. Уравнение , в котором правая часть тождественно равна нулю, называетсяоднородным линейным уравнением.

Общее решение неоднородного линейного уравнения находится подстановкой ,, гдеи- неизвестные функции от. Уравнение тогда примет вид. Приравняв нулю выражение в скобках, получим уравнение с разделяющимися переменными, из которого найдёмв виде его частного решения, где- какая-нибудь первообразная для. Подставив затем найденное выражениев уравнение, получим уравнение с разделяющимися переменными, из которого найдёмв виде его общего решения. В результате найдём и общее решение исходного уравнения в виде.

Некоторые уравнения становятся линейными, если поменять ролями искомую функцию и независимую переменную. Например, уравнение - нелинейное относительнои, является линейным относительнои:.

В задачах 9.47-9.62 найти общие решения следующих линейных дифференциальных уравнений:

9.47 . 9.48.

9.49 . 9.50.

9.51 . 9.52.

9.53 . 9.54.

9.55. 9.56.

9.57 . 9.58.

9.59 . 9.60

9.61 . 9.62.

В задачах 9.63-9.70 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:

9.63,. 9.64,.

9.65,. 9.66,.

9.67,.

9.68,. 9.69,.

9.70 ,.

Уравнение вида , гдеи, называетсяуравнением Бернулли. Оно приводится к линейному с помощью подстановки . Решение уравнения Бернулли можно также найти непосредственно подстановкой.

В задачах 9.71-9.78 найти общие решения уравнений Бернулли:

9.71 . 9.72.

9.73 . 9.74.

9.75 . 9.76.

9.77 . 9.78.

Уравнение называетсяуравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , т.е.. Это имеет место, если выполнено тождество.

Общий интеграл уравнения имеет вид , где- произвольная постоянная. Функциюнаходим, используя равенстваи. Сначала, интегрируем первое из равенств пои определяем функциюс точностью до произвольной дифференцируемой функциив виде, где- одна из первообразных для функции. Затем, подставляем это выражение дляво второе из равенств и получаем дифференциальное уравнение для определения функции:, интегрируя которое находимв виде его частного решения.

В задачах 9.79-9.86 решить следующие уравнения, предварительно убедившись, что они являются уравнениями в полных дифференциалах:

9.79 .

9.80 .

9.81 . 9.82.

9.83 .

9.84 .

9.85 ;.

9.86 ;.

Уравнения первого порядка , не разрешённые относительно производной, решают следующими методами.

1) Разрешаем уравнение относительнои получаем одно или несколько уравнений вида(), каждое из которых надо решить. Если решение уравнений найдено в виде общих интегралов, то общий интеграл исходного уравнения записываем в виде.

2) Метод введения параметра. Разрешаем уравнение относительнои записываем в виде. Вводим параметри получаем. Берём полный дифференциал от обеих частей равенстваи заменяячерез, получаем уравнение вида. Если решение этого уравнения найдено в виде, то учитывая равенство, записываем решение исходного уравнения в параметрическом виде:,. Уравнения видарешают таким же способом.

В задачах 9.87-9.92 разрешить следующие уравнения относительно и найти их общее решение:

9.87 .9.88 .