§2. Обыкновенные дифференциальные уравнения

высших порядков.

Уравнение вида , где- искомая функция, называетсядифференциальным уравнением -го порядка. Функция , обращающая уравнение в тождество, называетсярешением уравнения, а график этой функции – интегральной кривой. Если решение уравнения задано в неявном виде , то оно называетсяинтегралом уравнения.

Уравнение вида , называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ -го порядка называютнормальной.

Условия ,,…,, где,,,…,- заданные числа, называются начальными условиями. Задача нахождения решения уравнения , удовлетворяющего заданным начальным условиям, называетсязадачей Коши.

Общим решением ДУ -го порядка называется решение, зависящее отпроизвольных постоянных, такое, из которого при надлежащем выборе значений постоянныхможно получить решение, удовлетворяющее заданным начальным условиям,,…,. Общее решение, заданное в неявном виде, называетсяобщим интегралом уравнения.

Частным решением ДУ -го порядка называется решение, получаемое из общего при конкретных значениях постоянных. Частное решение, заданное в неявном виде, называетсячастным интегралом уравнения.

Если для искомого частного решения уравнениязаданы начальные условия,,…,и известно общее решениеуравнения, то значения произвольных постоянных определяются, если это возможно, из системы уравнений .

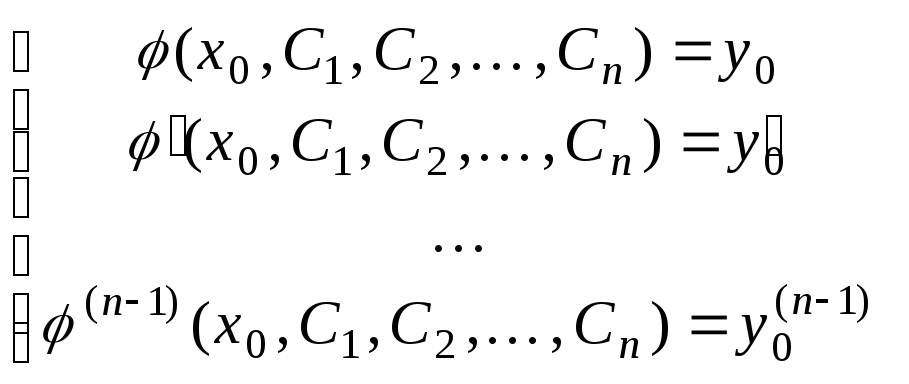Уравнение вида называетсяпростейшим дифференциальным уравнением -го порядка.Его общее решение находят, выполняя последовательно интегрирований, и записывают в виде

.

Уравнение вида ,, не содержащее явно искомой функции, с помощью подстановки, где- новая неизвестная функция, приводится к уравнениюпорядка.

Уравнение вида , не содержащее явно независимой переменной, с помощью подстановки, где- новая неизвестная функция от новой независимой переменной, приводится к уравнению порядка на единицу ниже. При этомпреобразуются так:,,…..

В задачах 9.131-9.150 найти общие решения дифференциальных уравнений, допускающих понижение порядка:

9.131 . 9.132. 9.133.

9.134 . 9.135. 9.136.

9.137 . 9.138.

9.139 . 9.140.

9.141 . 9.142.

9.143 . 9.144.

9.145 . 9.146.

9.147 . 9.148.

9.149 . 9.150.

В задачах 9.151-9.160 найти частные решения следующих уравнений при указанных начальных условиях:

9.151 ,,.

9.152 ,,,.

9.153 ,,.

9.154 ,,.

9.155 ,,.

9.156 ,,.

9.157 ,,.

9.158 ,,.

9.159 ,,.

9.160 ,,.

Функции ,,…,называютсялинейно зависимыми на , если существуют постоянные,,…,, не все равные нулю, такие, чтодля всех. Если равенство выполняется для всехтолько при условии, то данные функции называютсялинейно независимыми на .

Определитель 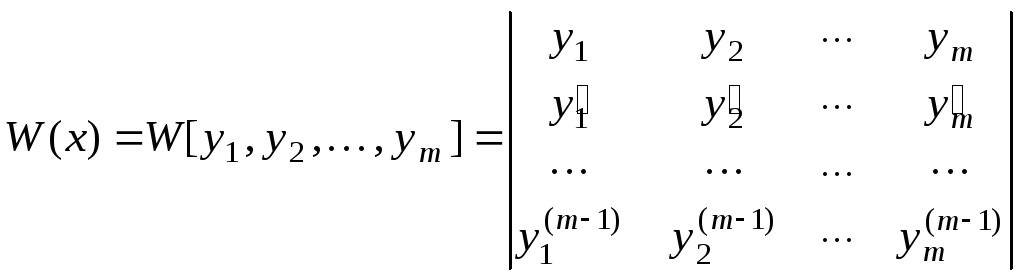называетсяопределителем Вронского (вронскианом).

Если функции ,,…,линейно зависимы на, то определитель Вронскогодля всех(необходимое условие линейной зависимости).

Если хотя бы в одной точке, то функции,,…,линейно независимы на(достаточное условие линейной независимости).

В задачах 9.161-9.170 исследовать, являются ли данные функции линейно независимыми (в каждой задаче функции рассматриваются в той области, в которой они все определены).