
- •Глава 9. Дифференциальные и разностные уравнения.
- •§1. Обыкновенные дифференциальные уравнения
- •9.1. 9.2.
- •9.23 . 9.24.
- •9.47 . 9.48.
- •9.89 . 9.90.
- •§2. Обыкновенные дифференциальные уравнения
- •9.131 . 9.132. 9.133.
- •9.161 ,. 9.162,.
- •9.163 ,. 9.164,,.
- •9.165 . 9.166,,. 9.167,,. 9.168,,. 9.169. 9.170.
- •9.171 . 9.172.
- •9.191 .
- •9.245 9.246
- •9.263 9.264
- •9.273 9.274
- •9.281 .
- •9.313. 9.314 .
- •9.323 . 9.324.
- •9.325 . 9.326.
- •9.327 . 9.328.
- •9.331 .
- •9.349 ,,;
- •10.1 . 10.2 .
- •10.3 . 10.4.
- •10.5 . 10.6.
9.191 .
9.192![]() .
9.193
.
9.193
![]() .
.
9.194
![]() .
.
9.195
![]() .
.
9.196
![]() .
9.197
.
9.197![]() .
.
9.198
![]() .
.
9.199
![]() .
.
9.200
![]() .
.
9.201
![]() .
9.202
.
9.202![]() .
.
В задачах 9.203-9.212 для каждого из неоднородных линейных дифференциальных уравнений с постоянными коэффициентами найти их общие решения:
9.203
![]() .
9.204
.
9.204![]() .
.
9.205![]() .
9.206
.
9.206![]() .
.
9.207
![]() .
9.208
.
9.208![]() .
.
9.209
![]() .
9.210
.
9.210![]() .
.
9.211
![]() .
9.212
.
9.212![]() .
.
В задачах 9.213-9.218 найти частные решения уравнений, удовлетворяющих указанным начальным условиям:
9.213
![]() ,
,![]() ,
,![]() .
.
9.214
![]() ,
,![]() .
.
9.215
![]() ,
,![]() ,
,![]() .
.
9.216
![]() ,
,![]() ,
,![]() .
.
9.217
![]() ,
,![]() ,
,![]() .
.
9.218
![]() ,
,![]() ,
,![]() .
.
В задачах 9.219-9.228 найти общие решения неоднородных уравнений методом вариации произвольных постоянных:
9.219
![]() .
9.220
.
9.220![]() .
.
9.221
![]() .
9.222
.
9.222![]() .
.
9.223
![]() .
9.224
.
9.224![]() .
.
9.225
![]() .
9.226
.
9.226![]() .
.
9.227
![]() .
9.228
.
9.228![]() .
.
В
задачах 9.229-9.244 найти
общие решения следующих дифференциальных
уравнений
![]() -ого
порядка:
-ого
порядка:
9.229
![]() .
9.230
.
9.230![]() .
.
9.231
![]() .
9.232
.
9.232![]() .
.
9.233
![]() .
9.234
.
9.234![]() .
.
9.235
![]() .
9.236
.
9.236![]() .
.
9.237
![]() .
9.238
.
9.238![]() .
.
9.239
![]() .
9.240
.
9.240![]() .
.
9.241
![]() .
9.242
.
9.242![]() .
.
9.243
![]() .
9.244
.
9.244![]() .
.
§3. Системы обыкновенных дифференциальных уравнений.
Система
дифференциальных уравнений вида
![]()
![]() ,
где
,
где![]() -
искомые функции, называетсянормальной
системой
дифференциальных
уравнений. Число
-
искомые функции, называетсянормальной
системой
дифференциальных
уравнений. Число
![]() называется
порядком
системы.
Совокупность
называется
порядком
системы.
Совокупность
![]() функций
функций
![]() ,
,![]() ,…,
,…,![]() обращающих каждое уравнение системы в
тождество, называетсярешением
этой системы.
обращающих каждое уравнение системы в
тождество, называетсярешением
этой системы.
Условия
![]() ,
,![]() ,…,
,…,![]() ,
где
,
где![]() ,
,![]() ,
,![]() ,…,
,…,![]() - заданные числа, называются
начальными условиями. Задача
нахождения решения нормальной системы
уравнений, удовлетворяющего заданным
начальным условиям, называется задачей
Коши.
- заданные числа, называются
начальными условиями. Задача
нахождения решения нормальной системы
уравнений, удовлетворяющего заданным
начальным условиям, называется задачей
Коши.
Общим решением нормальной системы ДУ называется решение:
![]() ,
,![]() ,…,
,…,![]() ,
,
зависящее
от
![]() произвольных постоянных
произвольных постоянных![]() ,
такое, из которого при надлежащем выборе
значений постоянных
,
такое, из которого при надлежащем выборе
значений постоянных![]() можно получить решение, удовлетворяющее
заданным начальным условиям
можно получить решение, удовлетворяющее
заданным начальным условиям![]() ,…,
,…,![]() .
Общее решение, заданное в неявном виде
.
Общее решение, заданное в неявном виде![]() ,
,![]() называетсяобщим
интегралом
системы.
называетсяобщим
интегралом
системы.
Частным
решением системы
называется решение
![]() ,
,![]() ,…,
,…,![]() ,
получаемое из общего при конкретных
значениях постоянных
,
получаемое из общего при конкретных
значениях постоянных![]() .
Если для искомого частного решения
системы заданы начальные условия
.
Если для искомого частного решения
системы заданы начальные условия![]() ,…,
,…,![]() и известно общее решение
и известно общее решение![]() ,,…,
,,…,![]() системы,
то значения
системы,
то значения![]() произвольных постоянных определяются,
если это возможно, из системы уравнений
произвольных постоянных определяются,
если это возможно, из системы уравнений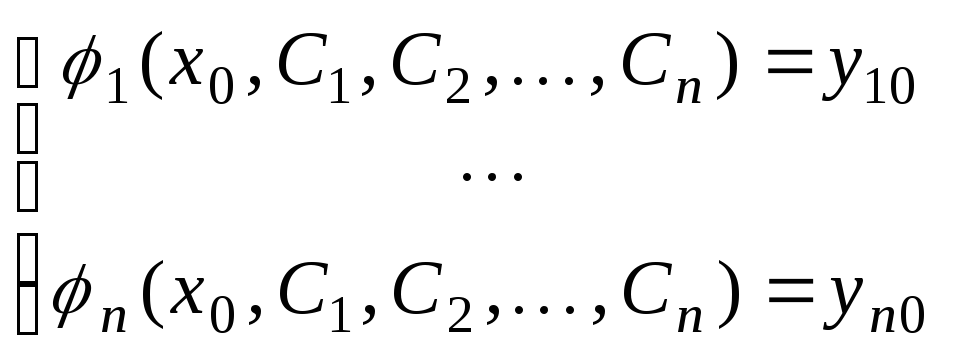 .
.
Нормальные
системы ДУ с небольшим числом уравнений
решают методом
исключения
неизвестных функций приводя их к одному
дифференциальному уравнению
![]() -го
порядка или к нескольким уравнениям
порядка, меньшего чем
-го
порядка или к нескольким уравнениям
порядка, меньшего чем![]() .
.
Для
нахождения решения, например, нормальной
системы двух уравнений
![]() ,
,![]() ,
где
,
где![]() ,
,![]() -
неизвестные функции независимой
переменной
-
неизвестные функции независимой
переменной![]() поступают следующим образом. Сначала
дифференцируют по
поступают следующим образом. Сначала
дифференцируют по![]() первое из уравнений системы и получают
уравнение
первое из уравнений системы и получают
уравнение![]() .
Затем определяют
.
Затем определяют![]() из первого уравнения системы и подставляют
найденное выражение
из первого уравнения системы и подставляют
найденное выражение![]() в уравнение
в уравнение![]() .
В результате получают ДУ второго порядка
относительно неизвестной функции
.
В результате получают ДУ второго порядка
относительно неизвестной функции![]() ,
решая которое находят
,
решая которое находят![]() ,
где
,
где![]() и
и![]() -произвольные постоянные. Подставляя
-произвольные постоянные. Подставляя![]() в формулу
в формулу![]() ,
определяют функцию
,
определяют функцию![]() .
Совокупность функций
.
Совокупность функций![]() ,
,![]() даёт общее решение системы.
даёт общее решение системы.
Однородной
линейной системой
![]() уравнений с
постоянными коэффициентами называется
система вида
уравнений с
постоянными коэффициентами называется
система вида
 или, в матрично-векторной записи
или, в матрично-векторной записи![]() ,
где
,
где![]()
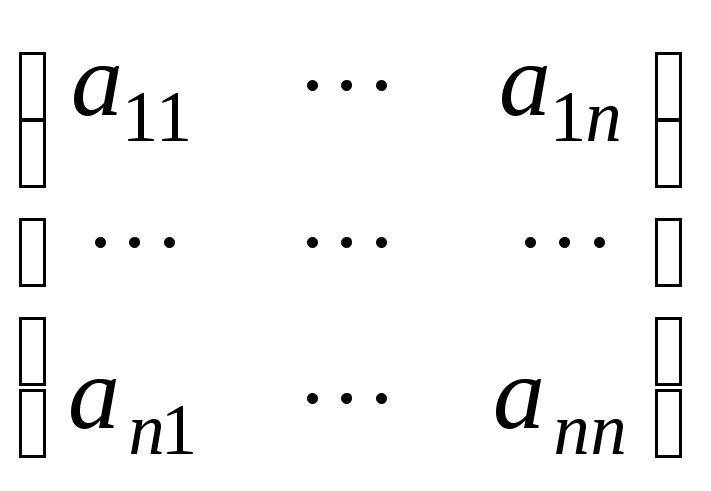 -
матрица системы,
-
матрица системы,![]() -
постоянные коэффициенты,
-
постоянные коэффициенты,![]() -
вектор неизвестных функций
-
вектор неизвестных функций![]() .
.
Для
построения общего решения однородной
линейной системы достаточно знать
![]() линейно независимых частных решений:
линейно независимых частных решений:
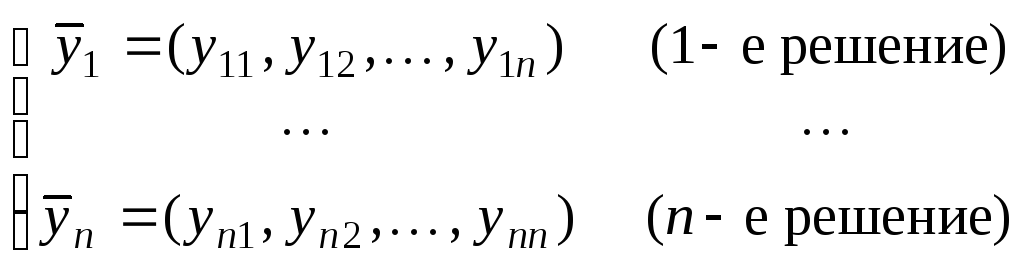 .
.
Такая система решений называется фундаментальной.
Если
известна фундаментальная система
решений (ФСР), то их линейная комбинация
![]() ,
где
,
где![]() - произвольные постоянные, представляет
собойобщее
решение однородной линейной системы
дифференциальных уравнений.
- произвольные постоянные, представляет
собойобщее
решение однородной линейной системы
дифференциальных уравнений.
Основным
методом построения фундаментальной
системы решений является метод
Эйлера.
Согласно этому методу частное решение
системы ищут в виде
![]() ,
где
,
где![]() -собственное
число матрицы
-собственное
число матрицы![]() ,
определяемое как кореньхарактеристического
уравнения
,
определяемое как кореньхарактеристического
уравнения
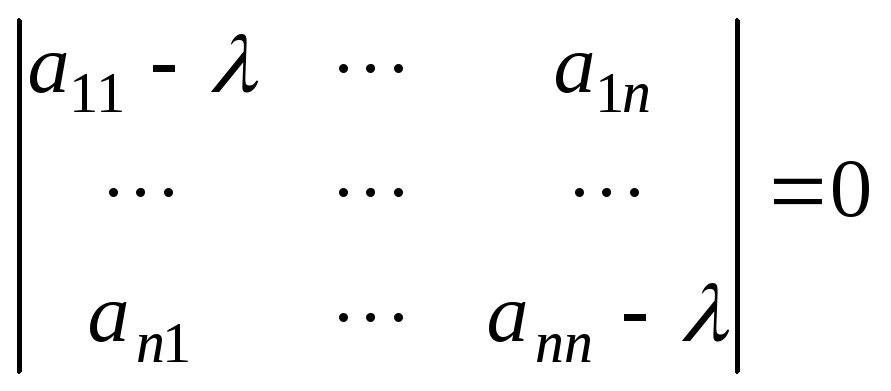 ;
;![]() - какой-нибудь собственный вектор этой
матрицы, соответствующий числу
- какой-нибудь собственный вектор этой
матрицы, соответствующий числу![]() и определяемый как ненулевое решение
системы линейных алгебраических
уравнений
и определяемый как ненулевое решение
системы линейных алгебраических
уравнений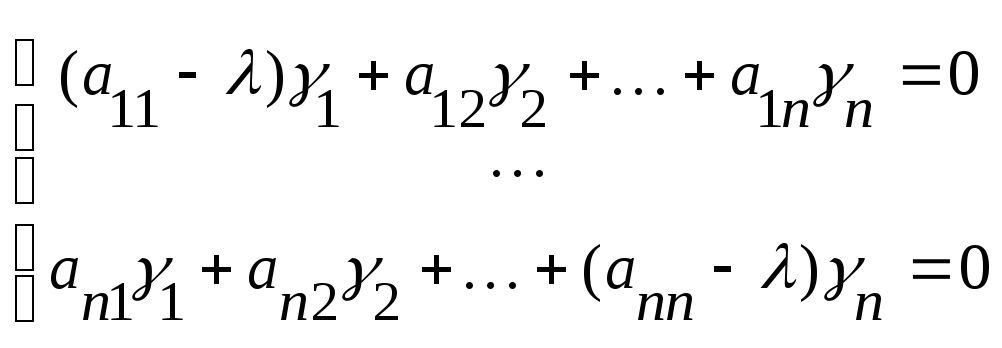 .
.
Каждому
из собственных чисел матрицы
![]() ,
являющихся корнями характеристического
уравнения, соответствует хотя бы одно
частное решение указанного вида, при
этом возможны следующие случаи:
,
являющихся корнями характеристического
уравнения, соответствует хотя бы одно
частное решение указанного вида, при
этом возможны следующие случаи:
1)
Если
![]() - действительный простой корень
характеристического уравнения, то ему
в ФСР соответствует одно частное решение
- действительный простой корень
характеристического уравнения, то ему
в ФСР соответствует одно частное решение![]() ,
где
,
где![]() - какой-нибудь собственный вектор матрицы
- какой-нибудь собственный вектор матрицы![]() ,
соответствующий числу
,
соответствующий числу![]() .
.
2)
Если
![]() - пара комплексно-сопряжённых простых
корней характеристического уравнения,
то ей в ФСР соответствует два линейно
независимых частных решения
- пара комплексно-сопряжённых простых
корней характеристического уравнения,
то ей в ФСР соответствует два линейно
независимых частных решения![]() ,
,![]() ,
где
,
где![]() - комплексный собственный вектор матрицы
- комплексный собственный вектор матрицы![]() ,
соответствующий комплексному собственному
числу
,
соответствующий комплексному собственному
числу![]() .
.
3)
Если
![]() - действительный корень кратности
- действительный корень кратности![]() характеристического уравнения, то
соответствующее ему решение, содержащее
характеристического уравнения, то
соответствующее ему решение, содержащее![]() произвольных постоянных
произвольных постоянных![]() и входящее в общее решение исходной
системы, ищется в виде произведения
векторного многочлена степени
и входящее в общее решение исходной
системы, ищется в виде произведения
векторного многочлена степени![]() на
на![]() :
:![]() . Чтобы найти векторные коэффициенты
. Чтобы найти векторные коэффициенты![]() ,
надо подставить данное решение в систему
,
надо подставить данное решение в систему![]() .
Приравняв коэффициенты подобных членов
в левой и правой частях уравнений
системы, получим систему линейных
алгебраических уравнений для определения
неизвестных координат векторов
.
Приравняв коэффициенты подобных членов
в левой и правой частях уравнений
системы, получим систему линейных
алгебраических уравнений для определения
неизвестных координат векторов![]() ,
причём среди координат этих векторов
,
причём среди координат этих векторов![]() координат являются произвольными и
полагаются равными
координат являются произвольными и
полагаются равными![]() ,
а остальные выражаются через них.
,
а остальные выражаются через них.
В задачах 9.245-9.252 найти методом исключения общие решения однородных систем дифференциальных уравнений:
