Физика / Теоритическая механика в задачах и примерах

		T 2 0,543 c.
		k
		Пример 12.2. Груз М массой m, подвешенный к
		концу пружины с коэффициентом жесткости с,
F	R	движется в жидкости. Сила сопротивления движению
		пропорциональна	первой	степени	скорости	груза
		R = V. Найти уравнение движения груза, если он в
	M	начальный момент был смещен из положения
V	P	статического равновесия вниз на х0 и ему была
		сообщена вниз начальная скорость V0.
		Решить задачу при следующих данных:
	x	m = 0,1 кг, с = 19,6 Н/м, = 0,6 Н с/м, х0 = 4 см,
		x0 = V0 = 4 см/c.

Рис. 12.2	Решение. Направим ось х вдоль пружины по
	вертикали вниз в сторону движения груза, выбрав
начало отсчета в его положении статического равновесия (рис. 12.2).
Запишем начальные условия движения груза:
t = 0,	х(0) = х0 = 4 см, x 0 x0 4 см/с.		(12.11)

Примем груз М за материальную точку и изобразим её в произвольном положении, при котором координата х положительна. На груз действуют

силы: сила тяжести P , сила упругости пружины F и сила сопротивления R

его движению, направленная противоположно скорости V груза, т. е. против оси х (рис. 12.2).

При х > 0 пружина получит удлинение равное + x, а проекция силы упругости F пружины на ось х будет равна

Fx = –c ( + x).

(12.12)

Запишем дифференциальное уравнение движения груза вдоль оси х

mx P Fx Rx .

Подставив в это уравнение Rx = – Vx и значение Fx из формулы (12.12), получаем

mx& P с cx Vx .

(12.13)

В положении статического равновесия х = 0 и уравнение равновесия

n

Fkx 0 принимает вид

k 1

P F		x 0	0	или	Р – с = 0.	(12.14)
Разделив (12.13) на m,			с	учетом	(12.14) и Vx x	получим
дифференциальное уравнение движения груза:

	&		&	k	2	x		0,	(12.15)
	x	2bx
где	b / 2m коэффициент,		характеризующий						сопротивление среды,
k	c / m соответствует частоте свободных колебаний груза в отсутствии

силы сопротивления.

Подставив численные значения, находим, что k = 14 с–1, b = 3 с–1; таким образом, b < k, т. е. имеет место случай малого сопротивления. Так как в этом

случае корни	характеристического		уравнения r2 2br k2 0 являются
комплексными	(r1,2 b i	k 2 b2 ),	то	тогда решение	уравнения (12.15)
запишем в виде		x Ae bt sin		k2 b2t .
					(12.16)
Вычислив производную по времени от (12.16), получим зависимость
скорости груза от времени:		b2t	k2 b2 Ae bt cos		k2 b2 t .
x& bAe bt sin k2

Подставляя в это выражение и в (12.16) начальные условия задачи (12.11) в общем виде и решая полученную систему алгебраических уравнений, находим формулы для вычисления постоянных интегрирования:

				x& bx				2
A	x2					0	0		,		(12.17)
					k2 b2
и начальной фазы	0
arctg				x	0	k2	b2			.	(12.18)
					x& bx			0
						0

Согласно (12.16) колебания груза являются затухающими (при t , х 0) с круговой частотой

k1	k2 b2 = 13,675 с–1.

Из условия задачи следует, что х0 = 4 см, x0 = 4 см/с. Подставив эти

численные значения в формулы (12.17) и (12.18), находим: А = 4,2 см,= 1,286 рад. Следовательно, груз совершает затухающие колебания (рис. 12.3) по закону

	x 4,2e 3t sin 13,675t 1,286				см.
x
0,04
0,03
0,02
0,01
0	0,4	0,8	1,2	1,6	2	t
0,01
0,02
0,03
		Рис. 12.3

Период Tc этих колебаний равен Tс = 2 /k1 = 0,459 с. Если бы груз совершал свободные колебания при отсутствии силы сопротивления, то

период его колебаний был бы меньше. Действительно, по формуле Т = 2 /k

получим	T = 0,449 с.
Пример 12.3. Решить задачу12.2 при следующих данных:
m		= –V0	= –2,4 см/c.
	= 0,1 кг, с = 19,6 Н/м, = 5,2 Н с/м, х0 = 4 см, x0

Решение. Начало отсчета оси х по-прежнему поместим в положение статического равновесия груза на пружине, направив ось х по вертикали вниз (рис. 12.2). В данном случае начальные условия движения груза имеют вид:

t = 0, x(0) = x0 = 4 см, x(0) x0 2,4 м/с.

Следуя решению предыдущей задачи, получим дифференциальное уравнение движения груза (12.15)

			2	x 0,
	x 2bx k
где k	c /m , b / 2m .

Подставив численные данные задачи, получим k = 14 с–1, b = 26 с–1; таким образом, b > k (случай большого сопротивления при b k ). Так как в

этом случае корни характеристического уравнения r2 2br k2 0 являются действительными (r1,2 b b2 k 2 ), то тогда решение дифференциального уравнения (12.15) следует искать в виде

x C1er1t C2er2t ,

(12.18)

где r1 b b2 k 2 , r2 b b2 k 2 .

Для определения постоянных интегрирования С1 и С2 вычислим скорость груза

	r1t	C2r2e	r2t	.	(12.19)
x C1r1e
Подставив в (12.18) и в (12.19) начальные условия движения t = 0,
х = х0, x x , получим систему уравнений:
0

	x0 С1			С2 ,
	x& С r С					r ;
		0	1 1			2 2
решая которую находим						r1x0 x0 .
С r2 x0		x0	,	С
1	r1 r2				2	r1	r2
Подставив в эти формулы				исходные			данные задачи	получим
С1 = – 0,059 и С2 = – 0,011, тогда уравнение движения груза будет
x	0,059e 47,909t				0,011e 4,091t .			(12.20)

По уравнению (12.20) построим график движения груза (рис. 12.4).

Рис. 12.4

Движение груза является апериодическим, при t , х 0.

Пример 12.3. На рисунке 12.5 изображена схема прибора для измерения давлений. К ползуну А массы m прикреплена стрелка В, отмечающая показания на неподвижной шкале С.

Ползун А, прикрепленный к концу пружины жесткости с, перемещается по гладкой горизонтальной плоскости. К ползуну приложена возмущающая горизонтальная сила H = H0 sin(pt). В начальный момент ползун находился в покое, в положении статического равновесия.

Определить уравнение движения стрелки В при отсутствия силы

сопротивления ее движению.

Решить задачу при следующих данных:

m = 0,2 кг;

с = 4 Н/м;

Н0 = 1,6 Н;

р = 20 с–1.

Решение. Введем ось х по

C

пружине

в направлении

ее

растяжения, взяв начало отсчета

B

в конце

недеформированной

пружины длиной l0.

с F

N

A

Начальные

условия

H

х

движения ползуна имеют вид:

l0 O

х

t = 0,

x 0

,

x& 0

.

P

0

0

Рассмотрим

ползун

в

Рис. 12.5

произвольном положении

х > 0,

при этом пружина растянется на величину х.

К ползуну приложены силы: P – сила тяжести, N – нормальная реакция гладкой горизонтальной плоскости, возмущающая сила H и F –

сила упругости пружины, проекция которой на ось х равна Fx = –cx (рис. 12.5).

Составим дифференциальное уравнение движения ползуна в проекции на ось х

mx H x Fx ,

или

&x Hm0 sin pt mc x .

Откуда получаем дифференциальной уравнение вынужденных колебаний в отсутствии сопротивления:

	&x k2x hsin pt ,			(12.21)
где k c / m ,	h H0 / m . Подставляя численные данные задачи находим
k = 4,472 с–1, h = 8 м с–2.
Уравнение	(12.21)	является	линейным	неоднородным

дифференциальным уравнением второго порядка с постоянными коэффициентами, поэтому его общее решение имеет вид

x = x1 + x2.	(12.22)
где х1 – общее решение однородного уравнения

&	k	2	x		0 ;	(12.23)
x

а х2 – частного решения уравнения (12.21).

Для уравнения (12.23) корни характеристического уравнения r2 + k2 = 0 являются мнимыми: r1,2 = ±ki. Поэтому решение уравнения (12.23) ищем в виде

x1 = C1 cos(kt) + C2 sin(kt).

(12.24)

Для определения закона вынужденных колебаний, т. е, частного решения х2 следует предварительно выяснить значение круговых частот свободных и вынужденных колебаний: k = 4,472 с–1, а р = 20 с–1, т. е. p ≠ k. Поэтому частное решение х2 надо искать в виде

x2 = Asin(pt) + Bcos(pt),

где А и В – коэффициенты, подлежащие определению. Подставив х2 в дифференциальное уравнение (12.21) и приравняв коэффициенты, стоящие

в левой и правой частях уравнения при одинаковых тригонометрических функциях, находим:

A			h		,	B = 0.
	k	2	p	2

Следовательно, частное решение принимает вид

x2				h		sin( pt).	(12.25)
		k	2	p	2

Воспользовавшись формулами (12.24) и (12.25), запишем общее решение (12.22) дифференциального уравнения (12.21)

x C cos(kt) C		sin(kt)	h	sin( pt).	(12.26)
			k2 p2
1	2

Для определения постоянных интегрирования С1 и С2 вычислим скорость ползуна:

x& C k sin(kt) C

k cos(kt)

hp

cos( pt).

(12.27)

k2 p2

1

2

Подставив в (12.26)

и (12.27) начальные условия движения: t = 0,

х (0)= 0, x 0,

и, решив

полученную систему алгебраических уравнений,

0

p

h

находим С1 = 0,

C2

.

k k

2

p

2

Следует обратить внимание на ошибку, которую часто совершают при вычислении постоянных интегрирования С1 и С2, подставляя начальные условия движения в общее решение (12.24) однородного уравнения вместо того, чтобы подставить их в общее решение (12.26).

Итак, уравнение движения ползуна и, следовательно, стрелки В имеет

вид

x

p

h

sin(kt)

h

sin(pt).

(12.28)

k k

2

p

2

k

2

p

2

Подставив численные значения р = 20 с–1, k = 4,472 c–1, h = 8 м с–2, получаем

x = (0,094sin 4,472t – 0,021sin20t) м.

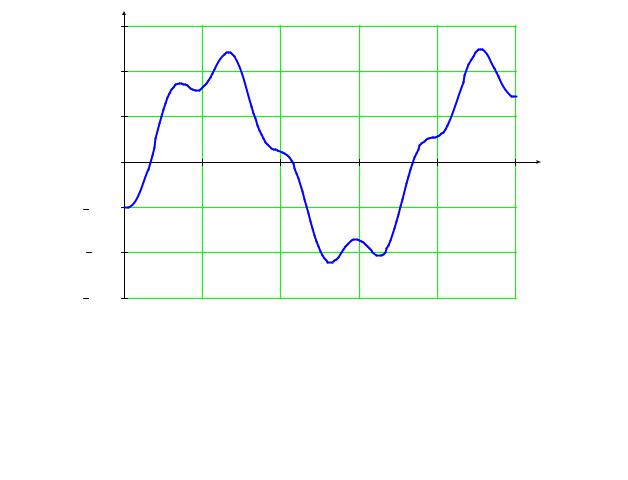
Рис. 12.6

Первое слагаемое в (12.28) соответствует колебаниям ползуна со стрелкой В с частотой k = 4,472 c–1 свободных колебаний, а второе слагаемое определяет вынужденные колебания с частотой р = 20 с–1, равной частоте

возмущающей силыH , при сложении которых получаем график движения стрелки В (рис. 12.6).

По теме «Прямолинейные колебания материальной точки» рекомендуем решить следующие задачи из сборника [1]: 32.4, 32.13, 32.16, 32.26, 32.64, 32.65, 32.66, 32.71, 32.72, 32.78, 32.80, 32.81, 32.96.

13. ТЕМА 15. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ТОЧКИ

На практическом занятии по теме «Динамика относительного движения» проводится решение двух задач динамики точки относительно неинерциальной системы отсчета, т. е. определяются или сила, или относительная скорость и закон относительного движения точки.

13.1. Задачи динамики относительного движения точки

Задачи динамики относительного движения материальной точки рекомендуется решать в следующем порядке:

1) разложить абсолютное движение материальной точки на относительное и переносное, выбрав неподвижную и подвижную системы отсчета, связанные соответственно с неподвижным телом и подвижной средой, относительно которой движется точка;

2)записать начальные условия относительного движения материальной точки;

3)изобразить на рисунке силыFк (активные и реакции связей), действующие на материальную точку;

4) найти ускорение aе		точки в переносном движении и ускорение
Кориолиса		r	и кориолисову
	aс ; а затем определить переносную Фе mae
r	r

Фс mac m 2 e Vr силы инерции, добавив их к действующим силам

Fk ;

5)составить дифференциальные уравнения относительного движения материальной точки в проекциях на оси подвижной системы координат;

6)проинтегрировать составленные дифференциальные уравнения, определив постоянные интегрирования с помощью начальных условий движения;

7)определить искомые величины.

При решении первой (прямой) задачи динамики точки, т. е. при определении сил по заданному движению, пункты 2) и 6) надо опустить.

Материальную точку следует изобразить в произвольном положении, соответствующем положительным значениям её координат, и предположить, что точка движется в сторону возрастания этих координат.

Пример 13.1. Груз А весом Р

спускается вниз по боковой грани

y

призмы В, расположенной под углом

O

N

к горизонту (рис. 13.1).

Fтр

Призма движется по

гладкой

A

горизонтальной плоскости направо с

e

Vr

Ф

ускорением а.

a

Определить ускорение ar груза

P

B

по отношению к призме и

и его

давление на ее боковую грань, если

х

коэффициент

трения

скольжения

груза о грань призмы равен f.

гладкой

Рис. 13.1

Решение.

Свяжем

с

горизонтальной плоскостью неподвижную систему координат (на рис. 13.1 не изображена), а с призмой В подвижную систему Оху, направив ось х вдоль боковой грани призмы вниз по вектору её скорости.

Движение груза А является сложным, так как оно складывается из относительного движения груза вниз по боковой грани призмы и переносное движение вместе с призмой В.

К грузу А приложены силы: сила тяжести P, нормальная реакция N боковой грани призмы и сила трения скольженияFтр , направленная в

сторону, противоположную скорости V движения груза.

Для решения задачи к этим действующим на точку силам добавить переносную силу инерции Фe и кориолисову силу инерции Фc .

Так как переносное движение является поступательным ( е = 0), то ускорение Кориолиса равно нулю (aс 0 ) и, следовательно, кориолисова

сила инерции Фс 0.

Переносная сила инерции Фе направлена в сторону, противоположную

вектору переносного ускорения a призмы В, т. е. по горизонтали налево (рис. 13.1) и равна по модулю

Фe mae ma.	(13.1)
Для определения величины ускорения ar (ar	x ) груза относительно
	&

боковой грани призмы составим дифференциальное уравнение его относительного движения в проекции на ось х:

mx Psin Fтр Фe cos .

Учитывая, что Fтр = fN и (13.1), находим

	&x g sinα	fN	a cosα.	(13.2)
		m

Для определения величины N нормальной реакции боковой грани призмы составим дифференциальное уравнение относительного движения груза в проекции на ось у %

my& N P cosα Фe sinα.

Так как ускорение груза в относительном движении ar = x и направлено перпендикулярно к оси у, то ary &y 0 . Тогда, с учетом (13.1) находим

N P cosα a / g sinα .

(13.3)

Искомое давление груза на боковую грань призмы направлено противоположно нормальной реакции N и равно ей по модулю. Подставив в уравнение (13.2) значение N из формулы (13.3), получим искомое