Физика / Теоритическая механика в задачах и примерах

координат ОXY и, подставив данные задачи и вычисленные выше модули ускорений, получим:

aaX ae arn cos30o arτ sin30o 0;

aaY arn sin30o arτ cos30o 74,6 см/c2. ;

Тогда модуль абсолютного ускорения точки М найдем по формуле:

aa aaX2 aaY2 74,6 см/c2 .

Следовательно, в момент времени t = 1 c величина абсолютного ускорения точки А aa 74,6 cм/c2 , а вектор aa 74,6 j направлен из точки А по оси ОY (по вертикали вверх).

5.2. Сложение вращений твердого тела вокруг пересекающихся осей

Задачи по определению абсолютной скорости точки твердого тела при сложении его вращений вокруг пересекающихся осей следует решать придерживаясь следующего порядка:

1. Выбрать неподвижную систему координат OXYZ так, чтобы её ось ОZ совпала с переносной угловой скоростью ωe , и подвижную систему координат Oxyz так, чтобы ось Oz совпала с относительной угловой скоростью ωr .

2. По известным векторам переносной ωe и относительной ωr угловых

скоростей найти абсолютную угловую скорость тела по модулю и направлению, а также положение мгновенной оси вращения ОР тела в данный момент времени.

3. Определить абсолютную скорость точки твердого тела как её скорость во вращении вокруг мгновенной оси ОР.

Пример 5.4 Карусель представляет собой круглую площадку АВ радиусом R, которая вращается вокруг оси ОС, проходящей через её центр D,

делая n1 об/мин, а ось ОС вращается в том же направлении вокруг

вертикальной оси ОЕ и делает n2 об/мин.

Определить абсолютную скорость точки В карусели в тот момент времени, когда она занимает самое низшее положение, если угол между осями ОС и ОЕ равен , а расстояние OD = l (рис. 5.5, а).

Решить задачу при следующих данных:

R = 5 м, n1 = 6 об/мин, n2 = 10 об/мин, = 20°, l = 2 м.

Решение. Рассмотрим положение карусели, когда точка В занимает низшее положение. Карусель совершает сложное движение, состоящее из

вращения вокруг оси симметрии ОС (относительное движение) и вращения её вокруг вертикальной оси ОЕ (переносное движение).

Свяжем с осью ОС ось Oz подвижной системы отсчета и направим по ней вектор относительной угловой скорости ωr (рис. 8.12, б), величина которого определяется по формуле

ωr π30n1 0,628 c-1 .

Ось ОZ неподвижной системы координат свяжем c вертикальной осью ОЕ и по ней направим вектор переносной угловой скорости ωe , модуль

которого равен

ωе π30n2 1,047 c-1 .

E

	C
A
D	R

B

l

O

а

Рис. 5.5

Z P

E A	L
	K

e

r

O

б

z C D

h

VB B

Результирующее абсолютное движение карусели является

вращательным движение с мгновенной угловой скоростью , равной геометрической сумме мгновенных угловых скоростей составляющих вращений

r r	(5.3)
ωr ωe .

На рис. 5.5, б вектор направим по диагонали параллелограмма, построенного на векторах ωr и ωe как на сторонах.

По теореме косинусов вычислим модуль мгновенной угловой скорости карусели:

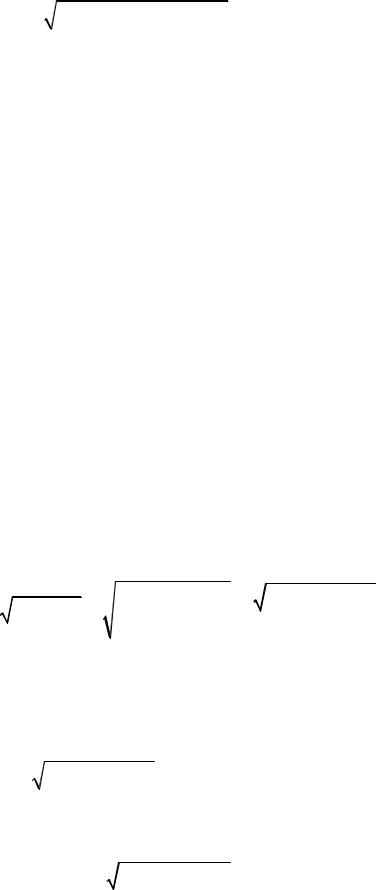
ω2r ωe2 2ωr ωe cosα 1,651 с-1 .

Прямая линия ОР, направленная по вектору мгновенной угловой скорости , является мгновенной осью вращения карусели в данный момент времени. Определим её положение, введя угол между векторами и ωr : по теореме синусов имеем

				ωe		,
	sin(180 o α)			sinβ
или		ωe sin α
	sinβ				.

Абсолютная скорость точки В карусели определим как её скорость во вращении вокруг мгновенной оси ОР. Для этого на рис. 5.5, б проведем из точки В на ось ОР перпендикуляр BK h . Тогда

VB h .	(5.4)
Вычислим h . В прямоугольном треугольнике BKL	KBL β (как острые

углы с взаимно перпендикулярными сторонами: BK , а BL ωr ). Тогда

где

h BL cosβ,

(5.5)

2

ω

sinα 2

2 ωe2 sin2 α

cosβ

1 sin

β 1

e

, (5.6)

а

sinβ

BL LD DB OD tgβ R l

R

cosβ

l

ωe sinα

R .

(5.7)

2

ωe2 sin2 α

Подставляя (5.5)–(5.7) в (5.4),

находим

VB l ωe sin α

R 2 ωe2 sin2 α 8,78 м/c .

Вектор абсолютной скорости VB точки В карусели лежит в плоскости,

перпендикулярной мгновенной оси ОР, и направлен перпендикулярно отрезку h в направлении абсолютного вращения с мгновенной угловой

скоростью (рис. 5.5, б).

5.3. Сложение вращений твердого тела вокруг параллельных осей

При решении задач на определение относительной, переносной и абсолютной угловых скоростей и различных скоростей точек планетарных и дифференциальных зубчатых передач рекомендуется придерживаться следующей последовательности действий:

1)выбирать одно вращение за относительное, второе вращение за переносное, а результирующее вращение за абсолютное;

2)записать для точки зацепления каждой пары колес, теорему о сложении скоростей, определив модули составляющих скоростей точки через относительные и переносные угловые скорости колес;

3)составить равенства, выражающие зависимости между абсолютными, переносными и относительными угловыми скоростями колес, из которых найти искомые величины.

Пример 5.5. На кривошип ОА (рис. 5.6, а), вращающийся вокруг оси О

сугловой скоростью ω , свободно насажена шестерня IV с числом зубцов z4

и две жестко связанные между собой шестерни II и III с числом зубцов z2 и z3 соответственно. Шестерня IV зацепляется с шестерней III, а шестерня II – с неподвижной шестерней I, имеющей z1 зубцов.

Определить абсолютную угловую скорость ω4 шестерни IV.

Решение. В данной задаче мы имеем так называемый планетарный зубчатый механизм.

Пусть кривошип ОА (водило) вращается вокруг неподвижной оси О против хода часовой стрелки; примем это вращение за переносное движение.

Относительные угловые скорости шестерен I, II, III и IV, т. е. угловые скорости их вращения по отношению к кривошипу ОА, обозначим

соответственно ω1 , ω2 , ω3 и ω4 . При этом ωi (i = 1, 2, 3, 4) будет принимать

положительное алгебраическое значение, если относительное вращение происходит против хода часовой стрелки, и отрицательное по ходу часовой

стрелки. Радиусы шестерен примем равными r1 , r2 , r3 и r4 .

Рассмотрим точку В зацепления шестерен I и II. Абсолютная скорость этой точки равна нулю, так как в точке В шестерня II сцеплена с неподвижной шестерней I:

VB VBe VBr 0 .

Поэтому

VBe VBr .

(5.8)

Переносная скорость точки В шестерни II равна по модулю VBe = ω r1 и направлена перпендикулярно ОВ в направлении вращения водила ОА.

	I
		II	III	e
			VC	IV
	VBe		VCr
	B		C
O		O		A
	VBr	1

а

'1

'2= '3 '4

B

C

4

OO1 A

I	II III	IV

б

Рис. 5.6

Тогда относительная скорость этой точки равна по величине VBr = ω2 r2

и направлена противоположно VB1e (рис. 5.6, а).

Из (5.8) также следует равенство модулей переносной и относительной скоростей точки В, т. е.

VBe VBr

или

	ω r1= ω2 r2 .
	Откуда	ω r1
	ω2 =		0.	(5.9)
		r2

Так как шестерни II и III жестко связаны между собой и представляют одно твердое тело, то

ω3= ω2 ,

(5.10)

и относительные вращения шестерен II и III совпадают с направлением вращения водила ОА, т. е. происходят против хода часовой стрелки (рис. 5.6,

б).

Рассмотрим теперь точку С зацепления шестерен III и IV. Найдем её абсолютную скорость

VC VCe VCr .

Переносная скорость точки С шестерни III по модулю равна VCe = ω OC и направлена перпендикулярно ОС в направлении вращения водила ОА. Относительная скорость этой точки численно равна VCr = ω3 r3 и направлена перпендикулярно O1C в направлении относительного вращения шестерни III

с угловой скоростью (рис. 5.6, а). Поэтому абсолютная скорость точки С шестерни III

VC VCe VCr ω OC ω3 r3 .

(5.11)

Подобным же образом находим, что абсолютная скорость точки шестерни IV, совпадающей с точкой С, по модулю равна

VC VCe VCr = ω OC ω4 r4 .	(5.12)
В этом случае относительная угловая скорость шестерни IV	ω4 < 0 ,

поскольку при внешнем зацеплении шестерен III и IV их относительные вращения происходят в противоположные стороны (рис. 5.6, б).

Приравнивая правые части (5.11) и (5.12), получаем

ω OC ω3 r3 ω OC ω4 r4

или

	ω3		r4		z4	,	(5.13)
	ω4		r3		z3

так как радиусы зубчатых шестерен пропорциональны числам их зубцов.

Следовательно, относительные угловые скорости двух сцепленных зубчатых колес обратно пропорциональны числам их зубцов и при внешнем зацеплении эти угловые скорости имеют разные знаки.

Из (5.13) находим

ω4 r3 ω3 r4

и с учетом (5.10) и (5.9) получаем

ω4		r3	ω2		r1	r3	ω.	(5.14)
		r4			r2
						r4

При сложении вращений тела вокруг параллельных осей из (5.6) следует, что абсолютная угловая скорость 4 шестерни IV равна алгебраической сумме переносной и относительной угловых скоростей:

							r1 r3
			ω4	ω + ω4 1						ω	,
							r2	r4
или
					z1	z3
				ω4 1				ω.			(5.15)
					z2
						z4
Если в (5.15)	z1	z3 / z2	z4 1, то 4 > 0 и направление абсолютного вращения
шестерни IV совпадает с направлением вращения водила ОА. При
соотношении	z1	z3 / z2	z4 1	4 < 0 и направление абсолютного вращения

шестерни IV противоположно направлению вращения водила.

По теме 6 «Составное (сложное) движение точки и тела» рекомендуется решить следующие задачи из сборника [1]: 22.14; 22.17; 22.18; 22.25; 23.7; 23.27; 23.28; 23.35; 23.36; 23.49; 24.1; 24.3; 24.4.

МОДУЛЬ 2 СТАТИКА

6. ТЕМА 8 СИСТЕМА СХОДЯЩИХСЯ СИЛ

На практическом занятии по теме «Система сходящихся сил» рассматриваются задачи на определение реакций связей несвободного твердого тела, которые можно решать геометрическим и аналитическим способами.

6.1. Равновесие твердого тела при действии плоской системы сходящихся сил

I. Геометрический способ решения рекомендуется проводить в следующем порядке:

1)выделить тело, равновесие которого следует рассмотреть для отыскания искомых величин;

2)изобразить заданные силы;

3)применив принцип освобождаемости от связей, приложить к твердому телу соответствующие силы реакций связей;

4)рассмотреть равновесие данного несвободного твердого тела как свободного тела, находящегося под действием заданных сил и реакций связей; согласно уравнению

r	n r
R Fк 0		(6.1)

к 1

построить силовой многоугольник (построение следует начинать с силы, известной как по модулю, так и по направлению);

5)геометрически решить силовой многоугольник и определить искомые величины.

Этим способом удобно пользоваться, если число задаваемых сил и сил реакций связей, приложенных к твердому телу, находящемуся в равновесии,

всумме равно трем; тогда задача сводится к построению и решению силового треугольника.

II. Аналитический способ решения задачи рекомендуется проводить в следующем порядке:

1)выделить тело, равновесие которого следует рассмотреть для отыскания неизвестных величин;

2)изобразить заданные силы;

3)применив принцип освобождаемости от связей, приложить к твердому телу соответствующие силы реакций связей; в дальнейшем рассматривать равновесие данного несвободного твердого тела как свободного тела, находящегося под действием заданных сил и реакций связей; убедиться, что данная задача является статически определимой, т. е. число неизвестных сил не более двух;

4)выбрать в плоскости действия сил систему декартовых координат ху; при этом оси целесообразно выбирать так, чтобы одна из искомых сил на

одну из осей (х или у) проецировалась в ноль; 5) составить уравнения равновесия тела в проекциях на оси координат:

n	n
Fkx 0,	Fky 0 .	(6.2)
k 1	k 1

6) решить полученную систему уравнений равновесия и определить искомые силы.

Если числовое значение какой-либо из неизвестных сил окажется отрицательной, то это означает, что в действительности направление силы противоположно тому, которое было указано на рисунке.

A

x

α

S1

C B y S2 Q

Q

Рис. 6.1

искомых усилий

Пример 6.1. Груз Q удерживается в равновесии двумя стержнями АС и ВС, соединенными между собой и с вертикальной стеной шарнирами (рис. 6.1).

Определить усилия в стержнях, считая их невесомыми, если углы, составляемые стержнями АС и ВС со стеной соответственно равны α и β.

Решить задачу при следующих данных:

Q = 300 Н, α = 30о, β = 60о.

Решение. Рассмотрим равновесие шарнира С, и изобразим действующие на него силы: сила тяжести

груза Q , S1 и S2 реакции невесомых стержней АС и

ВС соответственно, направленных по стержням в предположении, что они оба растянуты (рис. 6.1).

Шарнир С находится в равновесии под действием плоской системы сходящихся сил. Для определения

S1 и S2 можно воспользоваться геометрическим или

аналитическими условиями равновесия. Рассмотрим оба способа решения задачи.

1. Геометрический способ. Согласно (6.1)

Q S1 S2

0 ,

(6.3)

т. е. треугольник, построенный на этих силах, должен быть замкнут. Построение начинаем в произвольной точке плоскости с известной по

модулю и направлению силы Q . Через начало и конец вектора Q проводим

прямые, параллельные силам S1 и S2 . Точка пересечения этих прямых даст третью вершину треугольника. Направление обхода треугольника согласно

(6.3), т. е. направления векторов S1 и S2 , задает вектор

Q (рис. 6.2).

Заметим, что направление вектора S2 на рис. 6.2

противоположно его первоначально выбранному направлению на рис. 6.1. Это означает, что предположение о том, что в положении равновесия

S1

α

Q

S2

Рис. 6.2

стержень ВС растянут неверно; в действительности стержень ВС сжат.

Решим этот треугольник сил. Поскольку α 30o ,	β = 60о, то угол
между векторами S1 и S2 равен 90о. Определяем величины усилий S1 и S2
как катеты прямоугольного треугольника по известной	величине Q его

гипотенузы и острым углам α и β:

S1 Q cosα 260 H;

S2 Q cosβ 150 H.

Геометрический способ решения будет рациональным, если число действующих на тело сил равно трем, т. е. когда задача сводится к решению треугольников сил.

2. Аналитический способ. Проводим в точке С координатные оси: Сх по

стержню АС, а Су по стержню ВС, так как по условию задачи АСВ 90о

(рис. 6.1).

Записываем аналитические условия равновесия тела при действии плоской системы сходящихся сил (6.2):

n	n
Fкx 0 ;	Fкy 0 ,
к 1	к 1

и, проецируя уравнение (6.3) на выбранные координатные оси, получаем

Q cosα S1 0; Q cosβ S2 0.

Решая эти уравнения относительно S1 и S2 , находим

S1 Q cosα 260 H,

S2 Q cosβ 150 H.

Здесь знаки S1 и S2 означают, что стержень АС как первоначально

предполагали растянут, а стержень ВСсжат.

Пример 6.2. Балка АВ шарнирно закреплена на опоре А, а у конца В она положена на катки (рис. 6.3, а). В середине балки, под углом 450 к её оси,

действует сила Р . Определить реакции опор, пренебрегая весом балки. Решить задачу при следующих данных: