Физика / Теоритическая механика в задачах и примерах

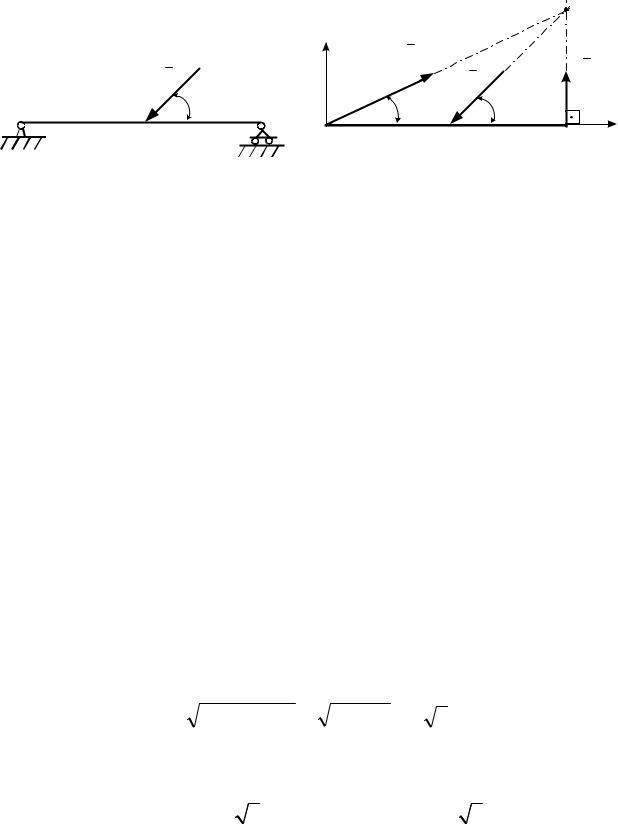
Р = 2 кН, АС = СВ = 2 м.
								O
P			y		RA	P		RB
		45o					45o
А			B					x
С				А	С			B
а			Рис. 6.3				б
Решение. Рассмотрим равновесие балки АВ находящейся под
действием силы Р .
Отбросим связи, заменив их действие реакциями связей. В точке В ре-
акция шарнирно-подвижной опоры RВ направлена перпендикулярно к
опорной поверхности.		По теореме о трех силах реакция RA					подшипника А
проходит через точку О пересечения линий действия сил						Р и RВ		(рис. 6.3,
б).
Следовательно, балка АВ находится под действием плоской системы
сходящихся сил. Для решения задачи введем декартовую систему координат
Axy и запишем аналитические условия равновесия (6.2) для рассматриваемой
задачи
RA cos P cos45o				0,				(6.4)
R	A	sin P cos45o		R	0,
				B

где угол, который реакция RA образует с осью Ах.

Вычислим входящие в (6.4) синус и косинус угла . Треугольник СВО является прямоугольным и равнобедренным СВ = ВО = 2 м. Из прямоугольного треугольника АВО по теореме Пифагора находим гипотенузу АО:

AO		AB 2 BO 2				42 22 2 5 м.
Тогда
cos		AB		2	,	sin	BO		1	.
		AO		5			AO		5

Из (6.4) определяем искомые реакции балки АВ:

RA

P cos45o

10

1,58

кН;

cos

2

R

P cos45o R

sin

2

0,71

кН.

A

B

2

ПРИМЕР 6.3. Определить модуль равнодействующей двух равных по величине сходящихся сил F1 F2 10 H , образующих между собой угол 60o

(рис. 6.4, а).

F2			R	y	F2
				F2
60o	F1	O	120o	O	60o	F1	x
O			F1
а			б				в

Рис. 6.4

Решение. 1. Геометрический способ. Построим по правилу сложения векторов равнодействующую

R F1 F2 ,

т. е. вектор, соединяющий начало первой силы F1 с концом второй силы F2

(рис. 6.4, б).

Тогда модуль равнодействующей R определим по теореме косинусов

R F12 F12 2F1F2 cos120o 17,3 H .

2. Аналитический способ. Введем в точке О декартовую систему координат Оху, направив ось Ох по силе F1 (рис. 6.4, в). Согласно (5.8) вычислим проекции равнодействующей R на декартовые оси:

Rх F1+ F2 cos60o = 15 H,

Ry F2 sin60o 8,66 H.

Тогда по формуле (5.10) найдем модуль равнодействующей R

R	Rx	2 Ry	2 = 152 8,662 17,3 H .
Геометрический способ решения такой задачи для системы сходящихся
сил будет рациональнее	аналитического, только тогда,			когда число

действующих сил равно двум, т. е. когда геометрическая задача сводится к решению треугольников сил.

6.2 Равновесие твердого тела при действии пространственной системы сходящихся сил

I. Решение задач на равновесие несвободного твердого тела, к которому приложена пространственная сходящихся система сил, рекомендуется проводить в следующем порядке:

1)выделить твердое тело, равновесие которого следует рассмотреть для отыскания искомых величин;

2)изобразить активные силы;

3)применив принцип освобождаемости от связей, приложить к твердому телу соответствующие силы реакций связей;

4)рассмотреть равновесие данного несвободного твердого тела как свободного тела, находящегося под действием активных сил и реакций связей;

5)выбрать декартовую систему координат;

6)записать уравнения равновесия для пространственной сходящейся системы сил в проекциях на выбранные оси:

n	n	n
Fkx 0,	Fky 0,	Fkz 0.;	(6.5)
k 1	k 1	k 1

6) решить полученную систему уравнений и определить искомые величины.

II. В задачах на определение равнодействующую пространственной системы сил требуется придерживаться следующей последовательности действий:

1)изобразить заданные силы;

2)ввести декартовую систему координат;

3)	найти проекции Rx , Ry , Rz	равнодействующей R на оси х, у, z;
4)	вычислить модуль равнодействующей по R формуле:
	R Rx2	Ry2 Rz2 ;	(6.6)

5) определить направляющие косинусы по формулам:

(6.7)

F1, F2,, F3 ,

	r r		R			r r
cos R i			x	,	cos R j
			R

Ry			r r		R
	,	cos R k			z	.
R
					R

Пример 6.4. Определить равнодействующую сил приложенных в вершине О прямоугольного параллелепипеда (рис. 6.5), если

углы образованные линиями действия сил			F2 и	F3 с	осями	координат
соответственно равны α и β.
Решить задачу при следующих данных:
F = 15 Н; F = 20 Н;		F = 25 Н; α = 60о; β = 45о.
1	2,	3
Решение. На прямоугольный параллелепипед						действует
пространственная	система	сходящихся сил	F1,	F2,, F3 .	Введем в точке
сходимости сил начало декартовой системы координат Охуz (рис. 6.5).
Для определения модуля равнодействующей R F1 F2 F3						вычислим
её проек-ции на декартовые оси:

R F cos(90o α) F cos0o F cos90o							z
х	1	2		3
	F1 sinα F2	33 H ;						F
								3
Ry F1 cosα F2 cos90o F3 cos 90o β						F	O	y
	F cosα F sinβ 25,2 H ;
	1	3				1		F2
	Rz F1 cos90o F2 cos90o F3 cosβ					x
	F3 cosβ 17,7 H .							Рис. 6.5
	Тогда согласно (6.6) модуль
равнодействующей равен:
		R	R 2	R 2	R 2	45,1 H .
			x	y	z

По формулам (6.5) вычислим направляющие косинусы углов

r r

R

r r

Ry

r r

R

cos R i

x

0,73;

cos R j

0,56;

cos R k

z

0,39;

R

R

R

Откуда		r r	o		r r	o
	R i		43 7 ;	R j		55 57 ;

	r r	67	o
R k			3 .

В декартовой системе координат равнодействующая сил F1, F2, , F3

равна R 33 i 25,2 j 17,7 k .

Пример 6.5. Три стержня АО, ВО и СО шарнирно-стержневой конструкции соединены в точке О.

Определить усилия, возникающие в стержнях под действием силы F ,

приложенной к шарниру О (рис. 6.6), если АВ = АО =							АА .
					Решить задачу при следующих данных:
		B	z		F = 12 H,		АВ = АО = АА = а.
				C	Решение. Рассмотрим равновесие
		S2			узла О, в котором соединяются стержни
			O		АО, ВО и СО.
		S1 450
A				у	Узел	находится		под	действием
		F	S3		силы	F ,	направленной			по
					пространственной диагонали куба, так
		х	450		как по условию АВ = АО = АА = а .
	B			C	Отбросим		стержни,		заменив	их
					действие	реакциями			S1 , S2 , S3 ,
					направленным по стержням в узел О
					предполагая,		что	в	положении
A			O		равновесия конструкции все стержни
		Рис. 6.6			сжаты.		О введем
					В точке				декартовую

систему координат Охуz, направив оси

по ребрам куба.

Вершина (далее узел) О находится в равновесии под действием пространственной системы сходящихся сил. Поэтому запишем аналитические условия равновесия (6.5) в общем виде и для данной задачи:

n	n	n
Fкx 0 ,	Fкy 0 ,	Fкz 0 ;
к 1	к 1	к 1

или

S2 cos 450 S3 cos 450 F cos cos 450 0,

S	S	2	cos 450 F cos sin 450	0,	(6.8)
1

S3 cos 450 F sin 0.

Здесь использовалось, что диагонали граней куба образует с его ребрами углы 450.

При определении проекций силы F на оси х и у применялся метод двойного проецирования: сначала силу F спроецировали на координатную

плоскость Оху, проекция которой Fху является вектором; затем этот вектор

Fху проецировали на оси координат Ох и Оу, расположенные в этой

плоскости.

Для решения системы уравнений (6.8) вычислим синус и косинус угла

между вектором силы F и плоскостью Оху:

AO

2

2

BO

a

2

,

OB

BB

BO

a

3 ;

cos 450

a

3

2

sin OO

;

cos O B

a

2 .

a

3

3

3

OB

OB

a

3

Тогда из третьего уравнения (6.8) находим

S3 F sin 0 4 6 9,8 Н. cos 45

Разделив первое уравнение системы (6.8) на соs 450, определяем

S2 = F cos S3 0 Н.

Из второго уравнения (6.8) вычисляем

S F cos sin 450	S	2	cos 450	4 3 Н.
1

Следовательно, в положении равновесия шарнирно-стержневой конструкции (рис. 6.6) стержни АО и СО сжаты, а стержень ВО не напряжен.

Пример 6.6. Конструкция состоит из невесомых стержней 1, 2,…, 6, соединенных дуг с другом в узлах H и L и с неподвижными опорами А, В, С

и D шарнирами (рис. 6.7). В узлах H и L приложены силы P и Q , образующие с координатными осями углы 1, 1, 1 и 2, 2, 2 соответственно (углы 2, 2, 2 на рисунке не показаны).

Грани параллелепипеда параллельные плоскости ху квадраты. Диагонали боковых граней образуют с плоскостью ху угол , а диагонали параллелепипеда составляют с этой же плоскостью угол (см. рис. 6.7).

Определить усилия N1 , N2 , …, N6 в стержнях 1, 2,…, 6 соответственно. Решить задачу при следующих данных:

Р = 80 Н; Q = 40 Н; 1 = 60°; 1 = 45°; 1 = 60°; 2 = 60°; 2 = 45°;2 = 45°; = 45°; = 60°.

	Решение. Рассмотрим рав-
	новесие узла Н, в котором схо-
	дятся три стержня 2, 3 и 4.
	На узел действует сила									и
									P
	реакции		2 ,		3 ,			4 , которые
		N		N			N
	направим		по соответствующим
	невесомым стержням 2, 3, 4 от узла
	Н, предполагая, что все стержни
	растянуты(рис. 6.7).
	Узел		Н			находится				в
	равновесии		под					действием
	пространственной							системы
	сходящихся сил, для которой
	аналитические							условия
Рис. 6.7	равновесия имеют вид

n		n	n
Fkx 0,		Fky 0,	Fkz 0. .
k 1		k 1	k 1
Составим эти уравнения равновесия для узла Н:
P cos 1 N2 cos N4 sin 0,
		N3 N4 cos 0,
P cos 1				(6.9)
	1	N2 sin 0.
P cos

Решим систему алгебраических уравнений (6.9) относительно искомых реакций N2 , N3 , N4 и, подставив численные данные задачи, находим:

N2 P cos 1 46,2 H,

sin

N4 P cos 1 N2 cos 65,3 H, sin

N3 = P cos 1 N4 cos = 103 H.

Теперь рассмотрим равновесие узла L. На него действует сила Q и реакции N1 , N2 , N5 , N6 , направленные от узла L по стержням 1, 2, 5 и 6 соответственно (рис. 6.7). Согласно аксиоме 4 статики реакция N2

направлена противоположно силе N2 и численно ей равна ( N2 = N2 = 46,2

H).

Узел L находится в равновесии под действием пространственной система сходящихся сил. Запишем уравнения равновесия (6.5) для данного узла:

Q cos 2

N1 N2 cos N5 cos cos 0,

N5 cos sin N6 0,

Q cos 2

(6.10)

N2 sin N5 sin 0.

Q cos 2

При определении проекций силы

5 на оси х и у пользуемся методом

N

двойного проецирования. Сначала проецируем

5 на плоскость

ху

и

N

получим вектор

5 , модуль которого равен N5 N5 cos ; затем вектор

5

N

N

проецируем на оси х и у и определяем искомые проекции силы

5

на эти

N

оси:

N5x = N5 cos = N5 cos cos ,

N5y = N5 sin = N5 cos sin .

Решим полученную систему алгебраических уравнений (6.10) и, подставив численные данные задачи, найдем усилия N5 N1 , N6 , возникающие в соответствующих стержнях:

N5 Q cos 2 N2 sin 78,9 Н, sin

N1 = (Qcos 2 + N2 cos + N5 cos cos ) = 78,2 H,

N6 = (Qcos 2 + N5 cos sin ) = 63,4 H.

Знаки показывают, что в положении равновесия конструкции стержни 1, 2 и 4 растянуты, а стержни 3, 5 и 6 сжаты.

По теме 8 «Система сходящихся сил» рекомендуется решить следующие задачи из сборника [1]: 2.11; 2.18; 2.24; 2.26; 2.29; 2.31; 6.4; 6.8; 6.10.

7. ТЕМА 9 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ

На практическом занятии решаются примеры на определение алгебраических моментов для плоской системы сил относительно точки с использованием теоремы Вариньона и алгебраических моментов пар; а также задачи на равновесие тела под действием системы пар.

7.1. Алгебраические моменты сил и пар сил

Задачи на вычисление алгебраических моментов для плоской системы сил относительно точки плоскости с использованием теоремы Вариньона рекомендуется проводить в следующем порядке:

1) Разложить силу в точке её приложения на две взаимно перпендикулярные составляющие параллельные или декартовым осям, или

заданным размерам тела:		F F F ;
2)	вычислить модули составляющих;
3)	применить теорему Вариньона:
		mO (F) =mO (F ) mD (F )	(7.1)
При действии на		тело системы пар с моментами	m1, m2 , ..., mn ,

лежащих в одной плоскости, следует применять теорему о сложении пар, т. е. о замене системы одной парой с моментом

n
M = mк .	(7.2)

к 1

Для решения задач на равновесие твердого тела под действием системы пар с моментами m1, m2 , ..., mn , лежащих в одной плоскости, необходимо применять условие равновесия:

		n
		mк =0.
		к 1
Пример	7.1.	Определить

алгебраический момент силы F относительно начала координат О декартовой системы, если известны проекции силы

Fx , Fy и координаты хА, уА точки А приложения силы.

(7.3)

y

F"

F

j

1

xA x

O

i

yA -1 A (3,-1)

F'

Рис. 7.1

Решить задачу при следующих данных:

F 5 H	,	F 10 H	,	x	A	3 м	,	y	A	1 м	.
x		y
Решение. Построим на рис.										7.1 в точке А (3, 1) вектор силы F ,

разложив его на составляющие параллельные осям Ох и Оу: F F F , где

F 5 i , а F 10 j .

Модули

этих составляющих

равны

модулям

проекций силы

F

на

F

Fx

5 H ,

F

Fy

10 H.

соответствующие декартовые оси:

Для определения момента силы F относительно начала координат О

воспользуемся теоремой Вариньона (7.1):

mО(F) mО(F ) mО(F )

Fx

yA

Fy

xA

25 H м.

F и T

Пример 7.2. Вычислить сумму алгебраических моментов сил

относительно точки D.

Сила F приложена в вершине В прямоугольника АВСD и составляет со

стороной АВ угол α, а сила

T в точке С и образует со стороной ВС угол .

Длины сторон прямоугольника равны DА = а и DС = b (рис. 7.2).

Решение. Разложим силу F

в

A

точке

В

на

две

взаимно

F

B

перпендикулярные составляющие

F

и

F

F , а силу

T

в

точке

С

на

составляющие T

и T .

F

Модули этих составляющих равны:

T

F F cosα ,

F F sinα, T T sinβ

и

T T cosβ.

T

D

C

По теореме

Вариньона

вычислим

T

моменты сил

F и

T относительно точки

Рис. 7.2

D:

mD (F) + mD (T ) mD (F ) mD (F ) +mD (T ) mD (T )

F DA F DС T DС

F cosα a (F sinα T cosβ) b.

Здесь mD (T ) 0 , так линия действия составляющей T пересекает точку D.