Физика / Теоритическая механика в задачах и примерах

Пример 18.2. Каркас платформы состоит из двух рам, соединенных цилиндрическим шарниром C. Верхний конец рамы АС жестко защемлен в бетонную стену, нижний опирается на цилиндрические подвижные опоры В.

Определить вертикальную реакцию защемления А при действии сил Р1 и Р2

(рис. 18.2).

	А	Р1 С	К
		l	h
			Р2
			B
		Рис. 18.2

r	1	δrС
A				К
А	С		l	h
RAy
			r2	P2
	rB			B

Рис. 18.3

Решение. Для решения задачи применим принцип возможных перемещений. Активными силами являются заданные силы Р1 и Р2 .

Для определения вертикальной реакции защемления RAy зададим точке

Авозможность двигаться в вертикальном направлении. С этой целью применим принцип освобождаемости от связей, заменив защемление в точке

Ажестким ползуном, перемещающимся в вертикальных направляющих

(рис. 18.3). Приложим в точке А искомую реакцию RAy .

Сообщим возможное перемещение δrА точке А по направляющей

ползуна вверх. При этом все точки рамы АС получат одинаковые вертикальные возможные перемещения δrС δrА, а угольник СВ совершит

плоское движение. Направив виртуальное перемещение δrB подвижной

опоры В по горизонтали, найдем положение мгновенного центра вращения К угольника СВ (в точке К пересекаются перпендикуляры, восстановленные из точек С и В к δrС и δrB ). Следовательно, возможным перемещением для

угольника СВ – поворот на угол вокруг точки К в плоскости рисунка по ходу часовой стрелки (рис. 18.3).

На основании принципа возможных перемещений (18.1) вычислим возможную работу активных сил Р1 , Р2 и вертикальной составляющей

реакции RAy на возможных перемещениях точек их приложения и приравняем ее нулю:

δ Аa RAy δrrA Р1 δrr1 Р2 δrr2 0,

или

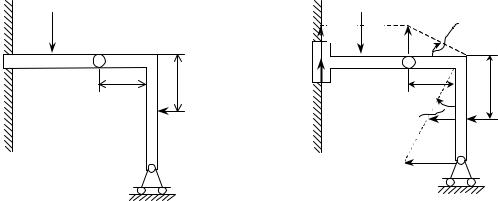
RАy δrА Р1 δr1 Р2 δr2 0,

(18.3)

где rA r1 rA.

Так как система имеет одну степень свободы (S = 1), то выразим величину r2 через rA, приняв это перемещение за независимое. При этом следует учитывать, что при стационарных связях возможные перемещения точек и тел связаны друг с другом как соответствующие скорости точек и тел системы при ее движении. Поэтому, так как VA = VC = l , то rA = rC = l ; значит, = rA/l. Следовательно, r2 = h = h rA/l. Подставив r2 в (18.3) получим

			Р	Р		h	0.
δr R
A	Ay		1		2	l
δrА 0, поэтому					h
RАy Р1			Р2			0 .
					l
Отсюда найдем вертикальную				составляющую реакции защемления
в точке А:						h .
RАy Р1				Р2
						l

На «Принцип возможных перемещений» рекомендуем решить следующие задачи из сборника [1]: 46.3, 46.6, 46.10, 46.14, 46.17, 46.22, 46.27.

18.2. Общее уравнение динамики

Общее уравнения динамики позволяет определять ускорения тел механической системы и составлять дифференциальные уравнения её движения. На практическом занятии задачи с помощью общего уравнения динамики рекомендуется решать в следующем порядке:

1)изобразить на рисунке активные силы и реакции, соответствующие неидеальным связям (например, силы трения);

2)определить главные векторы и главные моменты сил инерции масс системы.

Для системы с одной степенью свободы:

3)сообщить возможное перемещение одной из точек системы и выразить возможные перемещения точек приложения всех сил, указанных в первых двух пунктах, через это возможное перемещение, считая его независимым;

4)составить общее уравнение динамики:

n	r r	r	(18.4)
Fк Фк rк 0,

к 1

т. е. вычислить элементарную работу всех активных сил и сил инерции на возможных перемещениях точек системы и приравнять её нулю;

5) после сокращения полученного уравнения на независимое возможное перемещение определить искомую величину или провести интегрирование дифференциального уравнения движения.

Для системы с несколькими степенями свободы:

3) выбрать независимые возможные перемещения точек системы

вчисле, равном числу S степеней свободы этой системы;

4)сообщить возможное перемещение, соответствующее одной из степеней свободы системы, считая при этом возможные перемещения, соответствующие остальным степеням свободы, равными нулю. Выразить возможные перемещения точек приложения сил через это независимое возможное, перемещение;

5)вычислить сумму работ всех сил, указанных в пунктах 1) и 2), на соответствующих возможных перемещениях их точек приложения и приравнять ее нулю;

6)последовательно произведя выкладки пунктов 4) и 5) для каждого из независимых возможных перемещений, составить систему уравнений «равновесия» в числе, равном числу независимых возможных перемещений, т. е. числу степеней свободы системы;

7)после сокращения каждого из составленных уравнений на соответствующее независимое возможное перемещение можно определить из полученной системы уравнений искомые величины.

Пример 18.3. Каток A (рис. 18.4) массой m1, скатываясь без скольжения по наклонной плоскости вниз, поднимает посредством нерастяжимой нити

переброшенной через блок B груз C массой m2. При этом блок B вращается вокруг неподвижной оси Ox, перпендикулярной его плоскости материальной симметрии, проходящей через центр масс. Каток A и блок B – однородные круглые диски с одинаковыми массами и радиусами. Наклонная плоскость

образует с горизонтом угол . Определить ускорение центра масс катка A. Массой нити пренебречь.

Решение. Рассматриваемая система имеет одну степень свободы (S = 1), так как перемещение одного из тел приводит к однозначному перемещению всех других тел системы. Будем считать, что направления ускорений тел соответствуют направлениям их движения.

Изобразим активные силы: силы тяжести P1 – катка A и блока B и P2 –

груза C.

Приложим силы инерции. Силы инерции катка A, совершающего плоское движение, приводятся к главному вектору

	Φ A	m 1a A ,			(18.5)
	где aA – ускорение центра масс катка и к паре сил с моментом
	M Au		J Ax ε A .		(18.6)
				m R2
	Здесь A – угловое ускорение катка		A; J Ax	1	– момент инерции катка
				2

относительно оси Ax, проходящей через центр масс перпендикулярно плоскости движения. Отрицательные знаки в (18.4) и (18.5) указывают на то,

что сила инерции A и момент сил противоположно соответствующим ускорениям

SA

A

aАФАА MAи

P1

A

инерции M Au направлены aA и εA (рис. 18.4).

B

В
	В
О	MВи
P1	aC S
	C

СФС P2

	Рис. 18.4
		m R2
	Здесь A – угловое ускорение катка A; J Ax	1	– момент инерции катка
		2

относительно оси Ax, проходящей через центр масс перпендикулярно плоскости движения. Отрицательные знаки в (18.4) и (18.5) указывают на то,

что сила инерции A и момент сил инерции	M Au направлены
противоположно соответствующим ускорениям aA и εA	(рис. 18.4).
Силы инерции блока B, вращающегося вокруг неподвижной оси Ox с
угловым ускорением B, приводятся к паре сил, момент которой
M Bu J Ox ε B	(18.7)

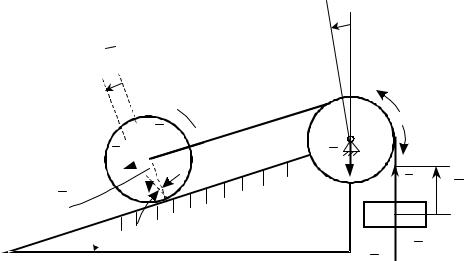
направлен противоположно угловому ускорению B. Здесь JOx m12R2 –

осевой момент времени блока B.

Сила инерции груза C, движущегося поступательно с ускорением aC ,

ΦC m 2aC .

Выразим ускорения, аС, B, A через искомое ускорение aA центра масс катка. Поскольку нить нерастяжимая, то aA = BR = аС. Следовательно,B = aA/R. Точка K катка A является для него мгновенным центром скоростей, поэтому A = aA/AK = aA/R. Тогда величины сил и моментов сил инерции тел системы определяется выражениями:

A = m1aА;

M Au m12R2 aRA m21R aA;

(18.8)

M Bu m12R2 aRA m21R aA ;

C = m2aА.

Сообщим телам системы возможные перемещения в направлении их движения и запишем общее уравнение динамики (18.4) для рассматриваемой задачи

P sin αδS

A

Φ

A

δS

A

M uδ

A

M u δ

B

P δS

C

Φ

C

δS

C

0, (18.9)

1

A

B

2

где SA и SC – величины возможных перемещений оси Ax катка A и груза C соответственно, A и В – углы поворотов катка A и блока B.

Поскольку система обладает одной степенью свободы, из всех возможных перемещений, входящих в (18.9), независимым будет лишь одно. Выберем за независимое возможное перемещение SA и выразим все остальные перемещения A, B, SC через SA. Зависимости между возможными перемещениями такие же, как и между соответствующими скоростями. Из кинематики известно, что

A = VA / R;

B = VА / R; VC = VA.

Следовательно,

A = SA/R,

B = SA /R,

SC = SA..

(18.10)

Уравнение (18.9) с учетом (18.10) имеет вид

δS

u

u

0,

P sin Φ

A

M A

M B P Φ

A 1

R

R

2

C

или, поскольку SA 0,

M Au

M Bu

P sin Φ

A

P Φ

C

0.

(18.11)

1

R

R

2

Подставив P1 = m1g, P2 = m2g и выражения (18.8) в (18.11), получим

m1g sin m1aA m12aA m12aA m2g m2aA 0.

Отсюда находим искомое ускорение центра масс катка А

aA g m1 sin m2 . 2m1 m2

Пример 18.4. К концам нерастяжимой и невесомой нити прикреплен груз А весом Р1, находящийся на горизонтальной плоскости, и груз В весом P2, расположенный на наклонной плоскости, которая составляет с горизонтом угол (рис. 18.5, а). От груза А нить идет через неподвижный блок С, охватывает подвижный блок D, а затем через блок Е, находящийся на одной оси с блоком С, идет к грузу В параллельно скату наклонной плоскости. К подвижному блоку D подвешен груз K весом Р3. Коэффициенты трения груза А о горизонтальную плоскость и груза В о наклонную плоскость соответственно равны f1 и f2.

Определить, пренебрегая массами блоков, ускорения грузов, полагая, что груз K опускается, а грузы А и В движутся, приближаясь к блокам С и Е.

Решение. Заданная механическая система состоит из трех грузов А, В и K, движущихся поступательно. Условимся определять положение грузов А, В и K соответственно координатами их центров масс x, s и y, отсчитываемых от начальных положений этих центров (рис. 18.5, б).

Нерастяжимая нить, связывающая грузы, накладывает на выбранные координаты следующее условие:

y = (x + s)/2.

(18.12)

Так как три координаты определяются одним уравнением, то независимыми являются из них две. Следовательно, рассматриваемая система имеет две степени свободы.

Примем координаты х и у за обобщенные координаты системы. Продифференцируем равенство (18.12) два раза по времени

y x s / 2 .

а

б

Рис. 18.5

Из полученного выражения следует, что алгебраические значения ускорений грузов имеют следующую зависимость

а3 = (а1 + а2)/2.

(18.13)

Здесь каждое ускорение положительно, если его направление совпадает с направлением выбранной оси координат, отрицательно – в противоположном случае.

Приложим к системе активные силы: P1, P2 , P3, а также силы трения F1, F2 , относя их к активным силам. Величина каждой силы трения равна

произведению коэффициента трения на нормальное давление между телами и плоскостью:

F1 = f1P1, F2 = f2P2cos .

Приложим в центрах масс грузов равнодействующие сил инерции их точек. Направим эти силы противоположно ускорениям, имеющим условно направление осей координат, и определим их модули:

Ф1 m1a1 Pg1 a1, Ф2 m2a2 Pg2 a2 , Ф3 m3a3 Pg3 a3 .

Сообщим системе возможное перемещение в сторону возрастания выбранных координат. Обозначим возможные перемещения грузов x, s иy. Согласно условию (18.12), эти перемещения связаны зависимостью:

y x s ; или s = 2 y – x. (18.14) 2

Составим общее уравнение динамики (18.4) для рассматриваемой механической системы

– (Ф1 + F1) x + (P3 – Ф3) y – (P2 sin + Ф2 + F2) s = 0.

Подставим в это уравнение модули сил инерции и сил трения, а также выразим s через x и y согласно (18.14), получим

P1

a

f P

x

P

P3

a1 a2

y

g

1

1 1

3

g

2

P sin

P2

a

f P cos

(2 y x) 0

2

2

g

2

2

или

		P1 a		f	P P			sin	P2 a	2	f	2	P cos			x
		g	1	1		1	2		g						2
	P			P3 a1		a2	2P sin 2				P2 a			2	2 f	2	P cos y 0.
		3		g		2		2			g						2

Так как x и y независимые возможные перемещения, то это равенство справедливо, если коэффициенты при этих приращениях координат равняются нулю. Приравнивая коэффициенты при x и y нулю, после несложных преобразований получаем:

P1a1 P2a2 P2 sin f2 cos f1P1 g,

P3a1 4P2 P3 a2 2P3 4P2 sin f2 cos g.

Решим эту систему уравнений относительно ускорений а1 и а2 грузов А

и В:

a1 g P2P3 2 sin f2 cos f1P1(4P2 P3) ,

P1(4P2 P3) P2P3

a2 g P1P3 2 f1 P2 (4P1 P3) sin f2 cos .

P1(4P2 P3) P2P3

Ускорение груза K определим по условию (18.13)

a3	a1 a2	g	P3 P1 P2 2P1P2 f1 sin f2 cos .
	2		P1(4P2 P3) P2P3

На «Общее уравнение динамики» рекомендуем решить следующие задачи из сборника [1]: 47.3, 47.5, 47.8, 47.9, 47.15, 48.26, 48.29, 48.30.

19. ТЕМА 23. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА

Наиболее общим методом составления дифференциальных уравнений движения механической системы являются уравнения Лагранжа второго рода.

При наличии идеальных связей, наложенных на систему, в эти дифференциальные уравнения не входят реакции связей, и при голономных связях, наложенных на систему, число составленных дифференциальных уравнений движения системы равно числу ее степеней свободы.

19.1. Решение задач с помощью уравнений Лагранжа второго рода

На практическом занятии	с помощью уравнений Лагранжа 2-го рода
определяют ускорения точек	(тел) системы,	а также составляют

дифференциальные уравнения её движения.

Составление уравнений Лагранжа второго рода рекомендуется проводить в следующей последовательности:

1)определить число степеней свободы материальной системы;

2)ввести независимые обобщенные координаты в количестве, равном числу S степеней свободы;

3)вычислить кинетическую энергию Т рассматриваемой механической системы как функцию обобщенных координат и обобщенных скоростей;

4)найти частные производные кинетической энергии по обобщенным скоростям q1, q2 , …, qs , т. е.

T	,	T	, …,	T	,
q1		q2		qs

а затем вычислить от них производные по времени:

d

T

d

T

d

T

,

, …,

;

dt

q1

dt

q2

dt

qs

5) определить частные производные кинетической энергии Т по обобщенным координатам: q1, q2, ..., qs, т. e.

	T	,	T	, …,	T		;
	q		q		q	s
	1		2

6) определить обобщенные силы системы Q1, Q2, ..., Qs соответствующие избранным обобщенным координатам;

7) полученные в пунктах 4), 5) и 6) результаты подставить в уравнения

Лагранжа второго рода
	d		T			T
							Qm	(m = 1, 2, …, S).	(19.1)
						qm
	dt		qm

Пример 19.1. Решить с помощью уравнения Лагранжа второго рода задачу, рассмотренную в примере 18.3: каток A (рис. 18.4) массой m1, скатываясь без скольжения по наклонной плоскости вниз, поднимает посредством нерастяжимой нити переброшенной через блок B груз C массой m2. При этом блок B вращается вокруг неподвижной оси Ox, перпендикулярной его плоскости материальной симметрии, проходящей