Физика / Теоритическая механика в задачах и примерах

	Ω VC		VC	3,46 c 1 .	(4.1)
			r cosα
	hP

Теперь найдем скорость точки В. Для этого на рис. 4.1 проведем из точки В перпендикуляр ВК на мгновенную ось ОР, равный по величине 2 hP .

Тогда скорость точки В определим как её скорость при вращении тела вокруг мгновенной оси:

VB Ω ВК Ω 2hP 2 VC 120 см/c .

Поскольку по условию задачи скорость VC точки С и расстояние hP постоянные по величине, то из (4.1) следует, что величина мгновенной угловой скорости также является постоянной. При качении конуса по

неподвижной плоскости	ХОY	конец вектора	(точка А) описывает
окружность радиуса .	Так как
		VA , тогда его модуль можно найти по
формуле
	ε VA ωZ Ω,		(4.2)

где ωZ – угловая скорость вращения конуса вокруг оси OZ.

Для определения ωZ проведем из точки С на ось ОZ перпендикуляр hZ (рис. 4.1), где

hZ OC cosα r ctgα cosα 30 см.

Тогда

ωZ VC 2 c 1, hZ

и из (4.2) находим

ε ωZ Ω 6,92 c 2 .

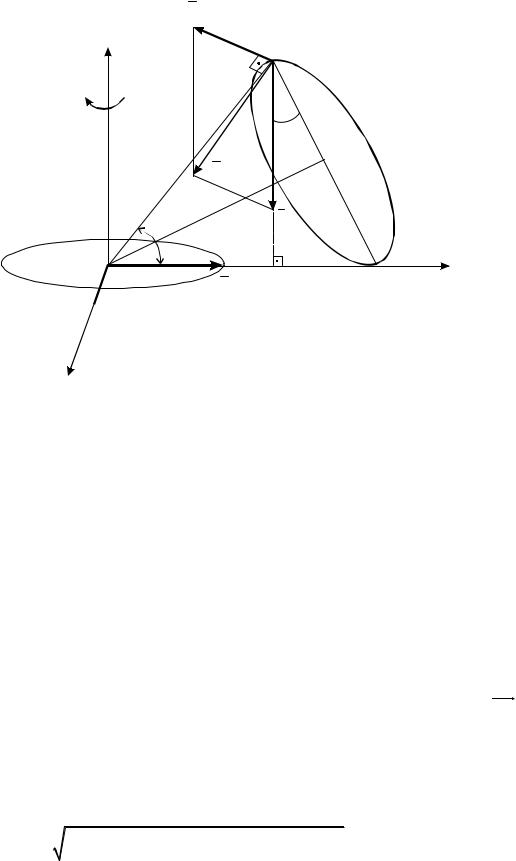
Изобразим на рис. 4.2 вектор углового ускорения ε конуса выходящим из точки О параллельно вектору VA , т. е. в данный момент времени ось углового ускорения ОЕ, по которой направлен вектор ε, совпадает с осью ОХ.

аBP

Z	B
Z
		C
	аB
	аОС	r
O	2 A	Y
	K	L P

X E

Рис. 4.2

Для определения ускорения точки В конуса воспользуемся теоремой Ревальса:

aB aOC aBP ,

где

aOC 2 BK 2 2hP 415,7 см/с2. aBP ε hE ε BO ε 2r 277,1 см/с2.

На рис. 4.2 вектор осестремительного ускорения аОС направим из точки В по BK к мгновенной оси вращения ОР. Вектор вращательного ускорения aBP

проведем перпендикулярно плоскости, проходящей через векторы ε и ОВ. Вектор ускорения aB точки В изобразим диагональю параллелограмма,

построенного на векторах аОС и aBP как на сторонах, модуль которого вычислим по формуле:

a

B

a2

a2

2 a

BP

a

cos

90o α

366 см/c2

.

BP

OC

OC

По теме 4 «Движение тела вокруг неподвижной точки» рекомендуется решить следующие задачи из сборника [1]: 19.1; 19.3; 19.5; 19.9.

5. ТЕМА 6 СОСТАВНОЕ (СЛОЖНОЕ) ДВИЖЕНИЕ ТОЧКИ И ТЕЛА

На практических занятиях по теме «Сложное движение точки и тела» решаются задачи по установлению соотношений между кинематическими характеристиками относительного, переносного и абсолютного движений точки и твердого тела.

5.1.Задачи на сложное движение точки

I.Если точка совершает сложное движение и составляющие движения,

вкоторых она одновременно участвует, заданы, то для определения кинематических характеристик её абсолютного движения следует придерживаться следующего порядка:

1)ввести две системы координат: неподвижную и подвижную, связанную с телом, относительно которого движется точка;

2)разложить движение точки на составляющие и определить её траектории в относительном, переносном и абсолютном движениях;

3)мысленно остановив переносное движение, найти положение точки в заданный момент времени на траектории относительного движения и определить её скорость и ускорение в относительном движении;

4)мысленно остановив относительное движение, по угловой скорости

иугловому ускорению переносного движения определить скорость и ускорение точки в переносном движении в заданный момент времени;

5)применив теорему о сложении скоростей, определить абсолютную скорость точки;

6)вычислить модуль ускорения Кориолиса и найти его направление, воспользовавшись правилом Н. Е. Жуковского;

7)найти проекции абсолютного ускорения точки на оси неподвижной системы отсчета и по ним определить искомое абсолютное ускорение точки по модулю и направлению.

II.Для определения одной из скоростей точки при сложном движении с помощью теоремы о сложении скоростей, если известны направления её абсолютной, относительной и переносной скоростей и модуль одной из этих скоростей, следует придерживаться следующего порядка:

1)ввести две системы координат: неподвижную и подвижную, связанную с телом, относительно которого движется точка;

2)разложить движение точки на составляющие и определить её траектории в относительном, переносном и абсолютном движениях;

3)воспользовавшись теоремой о сложении скоростей, построить в этой точке треугольник скоростей: построение следует начинать с вектора скорости, известной по модулю и направлению; затем через его конец и начало провести прямые, параллельные соответственно двум другим

векторам до их пересечения; при обходе полученного треугольника скоростей векторы, определяющие направления относительной и переносной скоростей, изображаются в одном направлении, а вектор абсолютной скорости – в противоположном;

4) найти модули неизвестных по величине скоростей, определив длины сторон в построенном треугольнике скоростей.

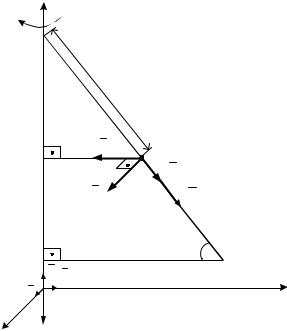
Пример 5.1. Пластина АВС равномерно вращается вокруг оси ОZ с угловой скоростью ωе (рис. 5.1). По её стороне АС движется точка М

согласно уравнению s =s(t)=АМ(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1.

Решить задачу при следующих данных:

ωе 10 с-1, s = АМ = 4t3 м, t1 = 0,5 c.

Решение. Точка М совершает сложное движение, поскольку она одновременно участвует в двух движениях.

Свяжем с осью вращения ОZ неподвижную систему координат ОXYZ, предполагая, что пластина АВС в рассматриваемый момент времени t1 находится в плоскости YОZ (рис. 5.1). Подвижную систему отсчета Axyz (на рис. 5.1 не изображена) мысленно свяжем с пластиной АВС, относительно которой движется точки М.

Тогда движение точки М по стороне АС вращающейся пластины АВС является для неё относительным движением, а вращение вместе с пластиной АВС вокруг неподвижной оси ОZ переносным движением (так как из

данных задачи ωе 0 , то пластина АВС вращается вокруг оси ОZ по часовой

стрелке).

Абсолютная скорость точки М вычисляется по теореме о сложении скоростей:

Va Vе Vr .

Сначала определим кинематические характеристики относительного движения точки. Это движение задано естественным способом и представляет собой прямолинейное движение точки М по стороне АС пластины АВС по

закону s = АМ =	= 4t3.
Найдем положение точки М на
траектории	относительного

движения в момент времени t1 = 0,5 c. Для этого вычислим расстояние

s1 AM t1 0,5 0,5 м.

Z
	e
A
	s1
K	Re	M
	Ve	Vr
B	Va	60o	C
O			Y
X
		Рис. 5.1

Определим относительную скорость точки М и ее численное значение:

Vr dsdt 12 t2 ,

при t1 = 0,5 c Vr = 3 м/с. Поскольку Vr 0, то на рис.5.1 вектор Vr

направим из точки М в сторону увеличения расстояния s = АМ, т. е. из точки М к точке С.

Вычислим величину переносной скорости точки М как скорость точки вращающейся пластины АВС:

Ve ωe Re ωe s1 cos60o 2,5 м/c ,

где Re = MK, т. е. длина перпендикуляра, опущенного из точки М на ось

вращения OZ, другими словами, Re – радиус окружности, которую описывала бы точка М при переносном вращении вместе с пластиной АВС вокруг оси OZ в данный момент времени t1 = 0,5 c.

На рис. 5.1 направим вектор Vе из точки М перпендикулярно отрезку MK в направлении ωе (параллельно оси ОХ).

Геометрически складывая векторы Vr и Vе , определяем вектор

абсолютной скорости Vа точки М. Так как угол между ними α 90о , то модуль абсолютной скорости находим по формуле:

Va Ve2 Vr2 3,9 м/с.

Для определения абсолютного ускорения точки М воспользуемся теоремой Кориолиса о сложении ускорений. Найдем векторы относительного, переносного ускорений и ускорения Кориолиса по модулю и направлению.

Так как относительное движение точки М задано естественным способом, то вектор относительного ускорения ar определяется по теореме Гюйгенса:

ar arτ arn .

Однако, поскольку траекторией этого движения является прямая линия АС

(		=		), то в этом случае величина нормального ускорения	an V 2		/ρ 0
					r	r

и ar arτ .

Z

Поэтому

значение

относительного

ускорения точки М

e

A

вычислим по формуле:

s1

τ

dV

24 t ,

ar ar

r

dt

K

R

an

M

2

e

e

и при t = 0,5 c ar 12 м/с .

aC

ar

Так как в данный момент

V

времени знаки числовых значений V и

r

ar

r

60o

одинаковые,

то

относительное

B

k j

C

движение точки ускоренное, и на рис.

O

Y

5.2

вектор относительного ускорения

X

i

e

ar

направим

так

же

как

вектор

относительной скорости Vr , т. е. из

Рис. 5.2

точки М к точке С.

Переносное ускорение точки М

определим как ускорение точки пластины АВС, вращающейся вокруг

неподвижной оси OZ:

r rn	r τ	,
ae ae	ae

где

ane ω2e Re 25 м/c2,

aeτ εe Re 0,

так как по условию задачи переносное движение равномерное вращение (ωe const ) и εe dωe / dt = 0. Следовательно, переносное ускорение точки М

r rn	, и на рис. 5.2 этот вектор
равно нормальному переносному ускорению ae ae

направим из точки М по отрезку MK к оси вращения OZ. Вычислим модуль ускорения Кориолиса

r

r

Vr ,

(5.1)

aС 2 ωe

который равен

r

aС 2

Vr

sinα 30 м/c

2

,

ωe

где α 30o угол между векторами ω

e

и V .

r

Направление вектора aC найдем

по правилу Н. Е.

Жуковского:

спроецируем вектор Vr относительной скорости точки М на плоскость ОХY,

перпендикулярную вектору ωe , а затем повернём эту проекцию в этой плоскости на 90о в направлении ωe (по ходу часовой стрелки). На рис. 5.2 изобразим вектор ускорения Кориолиса aC , направив его из точки М

параллельно оси ОХ.

Для определения абсолютного ускорения точки М запишем теорему Кориолиса о сложении ускорений для данной задачи:

aa aen ar aC .

Поскольку направление вектора абсолютного ускорения aa точки М

неизвестно, то в данном равенстве разложим его на составляющие векторы по осям декартовой системы ОХYZ:

rn		r r
aaX i aaX j aaX k ae	ar aC .
Здесь i , j, k орты неподвижного трёхгранника		ОХYZ (рис. 5.2), а aaX ,

aaY и aaZ проекции вектора aa на эти оси.

Проецируя полученное векторное равенство на оси ОX, ОY, ОZ и подставляя модули найденных выше векторов ускорений, получаем:

aaX aC 30 м/c2 ;

aaY aen ar cos60o 19 м/c2 ; aaZ ar sin60o 10,4 м/c2 .

Тогда модуль абсолютного ускорения точки М найдем по формуле:

aa aaX2 aaY2 aaZ2 302 ( 19)2 ( 10,4)2 37 м/c2 .

Следовательно, при t = 0,5 c модуль абсолютной скорости точки М равен Va 3,9 м/c , а величина её абсолютного ускорения aa 37 м/c2 .

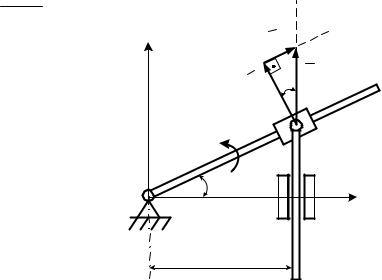
Пример 5.2. В кулисном механизме при вращении кривошипа ОL вокруг оси О, перпендикулярной плоскости рисунка, ползун А, перемещаясь вдоль кривошипа ОL, приводит в движение стержень АВ, движущийся в вертикальных направляющих K (рис. 5.3).

Определить абсолютную скорость Vа точки А в функции от угловой скорости ωи угла поворота кривошипа ОL, если OK = d.

Решение. Точка А ползуна совершает сложное движение, поскольку

она одновременно участвует в двух движениях.

Свяжем с точкой О и направляющими K неподвижную систему

координат OXY (рис. 5.3) . Тогда движение точки А вместе с поступательно

движущимся в вертикальных направляющих K стержнем АВ является для неё

абсолютным движением и поэтому вектор V

абсолютной скорости точки А

а

направлен вдоль направляющих по вертикали (параллельно оси OY).

Подвижную систему отсчета Оху мысленно свяжем с вращающимся

кривошипом ОL, по которому движется ползун А (на рис. 5.3 не изображена).

Тогда скорость той точки вращающегося кривошипа ОL, с которой в данном

положении механизма совпадает точка А, является для неё переносной

скоростью Vе . Поэтому вектор Vе

направлен из точки А перпендикулярно

кривошипу ОL в направлении его вращения с угловой скоростью .

Определим модуль переносной скорости точки А:

V ω OA ω

d

e

cos .

V

Y

Движение

точки

А

вместе

с

r

φ

Va

L

поступательно

движущимся

по

Ve

A

кривошипу ОL ползуном является для

неё

относительным

движением

со

скоростью Vr , направленной вдоль

кривошипа из точки А к точке L.

O

φ

K X

Для

определения

величины

абсолютной скорости Vа точки А

воспользуемся

теоремой

о

сложении

d

B

скоростей:

Va

Vе Vr .

Рис. 5.3

Для этого построим в точке А векторный треугольник скоростей.

На рис. 5.3 построение начинаем из точки А с известного по модулю и

направлению вектора переносной скорости Vе . Через его конец и начало

проводим прямые, параллельные соответственно векторам Vr

и Vа . Вектор,

проведенный из точки А в точку пересечения этих прямых, является

абсолютной скоростью точки А.

Полученный треугольник скоростей прямоугольный, так как Vе Vr .

Угол между векторами Vе

и Va

равен

,

как острые углы с взаимно

перпендикулярными сторонами (Vе

OA ,

а

Va OK ). Определим модуль

абсолютной скорости Va

точки А как гипотенузу данного прямоугольного

треугольника по известной величине катета Vе и углу :

V

Ve

ωd

,

a

cos

cos2

что и требовалось найти.

Пример 5.3. На тележке, движущейся по горизонтали вправо с

ускорением a0 , установлен электрический мотор, ротор которого при пуске в

ход вращается по закону = (t).

Определить абсолютное ускорение точки А, лежащей на ободе ротора

радиуса R, при t1, если в этот момент времени точка А находится в

положении, указанном на рис. 5.4.

Решить задачу при следующих данных:

а0 = 49,3 см/с2, = (t) = t2 рад, t1 = 1 c, СА = R = 20 см.

Решение. Свяжем с плоскостью, по которой движется тележка,

неподвижную систему координат ОXY, направив ось ОХ по направлению ее

движения, а с самой тележкой подвижную систему координат (на рис. 5.4

не изображена).

Точка

А

совершает

Y

сложное движение, поскольку

она одновременно участвует в

двух движениях: в переносном

ar

движении вместе

с тележкой

C

30o

ae

по

горизонтали

вправо

с

n

ускорением

a0

и

в

ar

A

относительном

вращении

с

a0

ротором вокруг оси С.

O

j

i

X

Для

определения

абсолютного ускорения точки

Рис. 5.4

воспользуемся

теоремой

Кориолиса

о

сложении

ускорений

aa aе ar aC .

Изобразим на рис. 5.4 в точке А уже известный по модулю вектор

r

r

2

, направленный параллельно оси

переносного ускорения ae

a0 49,3 см/c

ОХ. Найдем относительное ускорение точки А как ускорение точки

вращающегося ротора:

r rn	r τ
ar ar	ar .

Для этого вычислим угловую скорость и угловое ускорение ротора при t1 = 1 c:

ω	d	2t		t 1 2 c 1 ,	ε	dω	2 c 2 .
	dt					dt

Поскольку знаки угловой скорости и углового ускорения ротора оба положительные и угловое ускорение от времени не зависит, то ротор вращается равноускоренно против хода часовой стрелки (рис. 5.4).

Тогда величины нормального и касательного ускорений точки А в относительном движении равны:

arn ω2 R 80 см/c2, arτ ε R 40 см/c2.

	rn	направим из точки А по радиусу к оси С
Вектор нормального ускорения ar
вращения	ротора. Касательное	ускорение	rτ	изобразим	в	точке А
			ar
		rn	в направлении .
перпендикулярно нормальному ускорению ar
Так	как переносное движение поступательное (ωe 0),				то	из (5.1)

следует, что ускорение Кориолиса равно нулю (aС 0 ). Тогда в этом случае теорема Кориолиса принимает вид

r r r aa ae ar ,

или, поскольку относительное движение является вращательным,

r r rn	r τ
aa ae ar	ar .

Так как направление вектора абсолютного ускорения aa точки А

неизвестно, то в данном равенстве для плоского случая, разложим этот вектор на составляющие по осям ОХ и ОY:

aaX i aaX j	rn	r r	(5.2)
	ae	ar aC ,
где i , j орты неподвижной декартовой системы координат ОХY, а			aaX ,

aaY проекции вектора абсолютного ускорения aa на эти оси.

Для определения величины абсолютного ускорения точки А спроецируем векторное равенство (5.2) на оси неподвижной системы