Ответы на тестовые задания
|
Номер теста |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Правильный ответ |
3 |
2 |
1 |
2 |
2 |
1 |
1 |
1 |
2.3. Непрерывные функции одной переменной
Функция y
= f(x)
называется непрерывной в точке x0,
если она определена в некоторой
окрестности точки x0
и
f(x)
= f(x0).
Это определение содержит следующие четыре условия непрерывности:
1) y = f(x) должна быть определена в некоторой окрестности точки x0;
2) должны
существовать конечные пределы f(x0
+ 0) =
f(x)
и f(x0
– 0) =
f(x)
(пределы
справа и слева − односторонние пределы);
3) односторонние пределы должны быть одинаковыми;
4) эти пределы должны быть равны f(x0).
Если не выполняется хотя бы одно из условий 1–4, то функция имеет разрыв в точке x0.
Функция непрерывна в точке x0 справа, если выполняется условие
=
В противном случае
функция имеет разрыв в точке
справа.
Функция
непрерывна в точке
слева, если имеет место равенство
=
В противном случае
функция имеет разрыв в точке
слева.
Из условий 2–4 следует, что если функция непрерывна в точке x0, то она непрерывна в этой же точке справа и слева.
Критерий непрерывности функции
Функция y = f(x) непрерывна в точке x0 тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
=
Пример 1. Доказать, что функция f(x) = x2 – 1 непрерывна в точке x = 4.
Доказательство. Найдем значение функции в точке x = 4, f(4) = 15.
Вычислим предел:
–
= 16 – 1 = 15.
Получили, что предел функции в точке x = 4 равен значению функции в этой точке. Это означает, что условие непрерывности функции в точке выполнено, следовательно, данная функция непрерывна в точке x = 4.
Пример 2.
Доказать, что функция f(x)
=
непрерывна
в точке x
= 0.
Доказательство.
По условию f(0) = 0.
Произведение x sin
при
x
0 есть бесконечно малая величина как
произведение бесконечно малой x
на ограниченную величину sin
Предел бесконечно малой равен нулю,
следовательно,
Получили, что
т. е. данная функция непрерывна в точкеx
= 0.
Пример 3.
Доказать, что функция f(x)=
имеет
разрыв в точке x
= 1.
Доказательство. Значение функции в точке x = 1 есть f(1) = 1.
Найдем односторонние пределы функции в точке x = 1:
=
=
Получили, что в точке x = 1 предел слева не равен пределу справа, т. е. в этой точке предела не существует и функция при x = 1 имеет разрыв (рисунок 27).
Рисунок 27
Тест 1.
Функция f(x)=
1) имеет одну точку разрыва;
2) имеет две точки разрыва;
3) является непрерывной.
Тест 2.
Функция f(x)=
1) имеет одну точку разрыва;
2) имеет две точки разрыва;
3) является непрерывной.
Тест 3.
Точкой разрыва функции f(x)=
является:
1) 1;
2) 2;
3) –1;
4) –2.
Тест 4.
Точками
разрыва функции f(x)=
являются:
1) 4, 3;
2) 16, 9;
3) 4, –4;
4) 3, –3.
Тест 5.
Точкой разрыва функции f(x)
=
является:
1) 1;
2) 2;
3) 0;
4) нет точек разрыва.
Тест 6.
Точкой разрыва функции f(x)=
является:
1) 5;
2) 2;
3) 3;
4) нет точек разрыва.
Точки разрыва функции и их классификация
Если условия непрерывности функции в точке x0 не выполнены, т. е. в точке x0 существует конечный предел, не равный значению функции в этой точке, либо равный бесконечности, либо вообще не существует, то говорят, что функция имеет разрыв в этой точке.
Различают
точки разрыва первого рода и точки
разрыва второго рода. Если функция в
точке x0
имеет конечные пределы слева и справа,
из которых хотя бы один не равен
f(x0),
то точка x0
называется точкой разрыва первого
рода
функции f(x),
а величина
–скачком
функции в точке
x0.
Если при этом
то точкаx0
называется устранимой
точкой разрыва функции f(x),
так как, заменяя ее значение x0
в точке x0
общим значением
получим непрерывную функцию.
Если хотя бы один
из односторонних пределов
равен бесконечности или не существует,
тоx0
называется точкой разрыва второго
рода функции
f(x).
Пример 4.
Функция f(x)=
при x
≠ 0 непрерывна
как отношение двух непрерывных функций.
Полагая f(0)
= 1 в соответствии с пределом
получим функциюf(x)=
непрерывную
и в точке x
= 0.
Пример 5.
Исследовать на непрерывность функцию
f(x)=
Решение
Функция элементарная,
определена и непрерывна на всем множестве
действительных чисел, за исключением
точки x
= 2. В этой точке функция имеет разрыв.
Найдем предел
=
отсюда f(2
+ 0) = f(2
– 0) = 4.
Таким образом, в точке x = 2 функция имеет устранимый разрыв 9 (рисунок 28). Если эту функцию доопределить в точке x = 2, положив f(2) = 4, то она будет непрерывной на всей числовой прямой. В этом случае говорят, что функцию f(x) доопределили по непрерывности в точке x = 2.
Рисунок 28
Пример 6. Исследовать на непрерывность функцию
f(x)
=
Решение
Функция имеет
разрыв второго рода в точке x
= 0 с обеих сторон, так как
Тест 7.
Функция f(x)
=
1) имеет разрыв первого рода;
2) имеет разрыв второго рода;
3) является непрерывной.
Тест 8.
Функция f(x)
=
1) имеет разрыв первого рода;
2) имеет разрыв второго рода;
3) является непрерывной.
Тест 9.
Функция f(x)
=
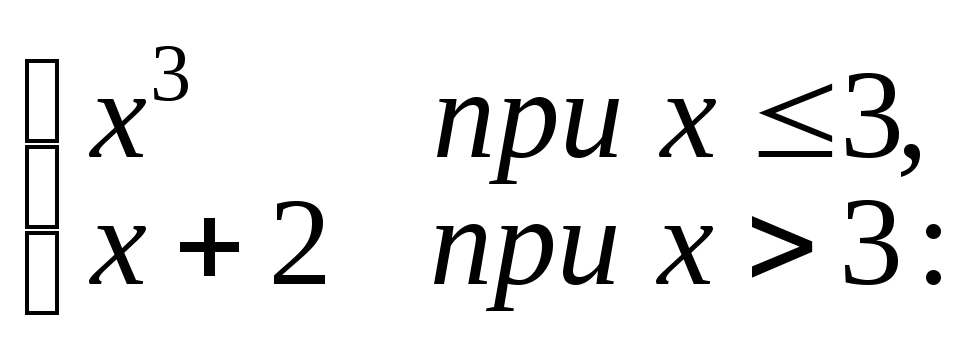
1) имеет разрыв первого рода;
2) имеет разрыв второго рода;
3) является непрерывной.
Тест 10.
Функция f(x)
=
в точке x
= 2:
1) имеет устранимый разрыв первого рода;
2) имеет разрыв первого рода;
3) имеет разрыв второго рода;
4) является непрерывной.
Тест 11.
Функция f(x)
=
в точке x
= 0:
1) имеет устранимый разрыв первого рода;
2) имеет устранимый разрыв второго рода;
3) имеет разрыв второго рода;
4) является непрерывной.
Рассмотрим свойства функций, непрерывных в точке:
1. Если функции f(x) и g(x) непрерывны в точке х0, то их алгебраическая сумма f(x) + g(x), произведение f(x) g(x) и частное f(x) / g(x) (при условии g(x) ≠ 0) являются функциями, непрерывными в точке х0.
2. Если функция y = f(x) непрерывна в точке х0 и f(х0) > 0, то существует такая окрестность точки х0, в которой f(x) > 0.
3. Если
функция y
= f(u)
непрерывна в точке u0,
а функция u
= (x)
– в точке х0,
то сложная функцияy
= f(φ(x))
непрерывна в точке х0.
Функция y = f(x) называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества. Все элементарные функции непрерывны в области их определения.
Функция y
= f(x)
называется непрерывной на отрезке [a;
b],
если она непрерывна в каждой внутренней
точке отрезка (a < x < b)
и
Рассмотрим свойства функций, непрерывных на отрезке:
1. Если функция y = f(x) непрерывна на отрезке, то она ограничена на этом отрезке.
2. Теорема Вейерштрасса: если функция y = f(x) непрерывна на отрезке [a; b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М.
3. Теорема
Больцано-Коши: если функция y
= f(x)
непрерывна на отрезке [a;
b]
и принимает на его концах значения
противоположных знаков, то для некоторого
Тест 12.
Функция f(x)
=
является непрерывной на отрезке:
1) [–5; 0];
2) [0; 5];
3) [–2; 2];
4) [1; 10];
5) имеет разрыв на каждом из указанных отрезков.
Тест 13.
Функция f(x)
=
является непрерывной на отрезке:
1) [–5; 0];
2) [0; 5];
3) [–1; 0];
4) [1; 10].
Тест 14.
Функция f(x)
=
является непрерывной на отрезке:
1) [–5; 0];
2) [2; 5];
3) [–2; 0];
4) [–10; 10].
Тест 15.
Функция f(x)
=
является непрерывной на отрезке:
1) [–5; 0];
2) [0; 5];
3) [–5; 5];
4) [5; 9].