Контрольные вопросы

1. Для чего в задаче о нахождении наикратчайшего расстояния необходимо проводить преобразование матрицы?

2. С помощью каких методов и почему решается задача нахождения наикратчайшего расстояния?

3. Почему задачу нахождения наикратчайшего расстояния можно представить как транспортную задачу?

4. Какая процедура используется в EXCEL «Поиск решения» для решения задачи о нахождении наикратчайшего расстояния?

5. При частном решении матрицы каким образом обозначается случай, когда между соответствующими вершинами нет пути?

6. Что представляют собой буферные емкости и какой величины они должны быть?

7. Каким образом из задачи о нахождении наикратчайшего расстояния получают транспортную задачу, представляющую задачу о назначениях?

Практическое задание № 5. Размещение проектируемого объекта

Задание. Определить местоположения проектируемого объекта (помещения) в производственном здании.

1. По последней цифре номера зачетной книжки (студенческого билета) выбрать номер варианта.

2. По номеру варианта (табл. 5.1) выбрать соответственно количество производственных помещений, координаты каждого помещения и размещаемого объекта.

Замечание. Значения координат объектов могут быть как положительными числами, так и отрицательными.

Решить задачу методом Ньютона с помощью «Поиска решения» программы МS ЕХСЕL:

- создать на листе MS EXCEL макет задачи размещаемого объекта, подписать ячейки с входными и выходными данными;

- внести нужные формулы;

- показать графическое расположение производственных помещений и размещаемого объекта;

- выделить на графике имеющиеся помещения и размещаемый объект в виде квадратиков;

- получить решение задачи и сделать соответствующие выводы.

Таблица 5.1

№ варианта	Количество производственных помещений	Координаты производственных помещений	Проектируемое (размещаемое) помещение
0	3	(3,-4), (6,-8), (18,20)	Сырьевой цех
1	4	(3,-6), (7,-10), (15,18), (26,-5)	Кладовая сухих продуктов
2	5	(4,-6), (8,-12), (16,11), (12,-24), (24,-48)	Компрессорная
3	6	(5,-5), (10,-10), (1,-20), (15,-15), (20,-7), (30,-2)	Отделение дробления кости
4	7	(0,-5), (5,-10), (10,-20), (15,-15), (19,-7), (28,-2), (30, 10)	Отделение приготовления рассола
5	8	(-10,-5), (10,-1), (1,-20), (15,-15), (20,-17), (30,-2), (25,-30), (5,-10)	Сушильная камера
6	4	(11,-5), (20,-10), (30,-20), (15,-15)	Моечная инвентаря
7	5	(5,-6), (10,-11), (1,-22), (15,-17), (20,-20)	Камера накопления и зачистки туш
8	6	(8,-5), (11,-14), (1,-25), (15,1), (20,-9), (30,-25)	Аппаратное отделение
9	5	(7,-5), (10,-10), (1,-20), (15,-15), (-4,10)	Машинное отделение

Работа рассчитана на 1 аудиторный час.

Постановка задачи о размещении объекта

Задача о размещении объекта относится к классу задач нелинейного программирования и является примером задачи многомерной нелинейной оптимизации. В математической модели этой задачи используются две независимые переменные, каждая из которых представляет отдельную координату точки на плоскости.

Задача может иметь несколько возможных вариантов постановки, отличающихся друг от друга количеством производственных помещений и их расположением на координатной плоскости.

Рассмотрим конкретно один из вариантов этой задачи.

Имеются четыре производственных помещения, расположенных на некотором производстве. Определить местоположение объекта (помещения) для размещения. Для примера объектом размещения выберем новый склад.

Требуется разместить новый склад в удобном для рабочих месте, предполагая, что сумма расстояний от нового объекта до всех производственных помещений будет минимальным значением (рис. 5.1). Это значение и является целевой функцией, которую необходимо определить, используя функции среды MS EXCEL.

Рис. 5.1.

Другие варианты задачи о строительстве или размещении объектов могут быть сформулированы как для различных значений количества производственных помещений, местоположения этих помещений, так и для различных видов целевой функции.

Математическая постановка задачи о местоположении объекта

Для математической постановки задачи следует ввести обозначения четырех координат, используя прямоугольную систему координат, в которой исходные производственные помещения и склад будут представлять отдельные точки на плоскости (рис. 5.2).

x₁ x₂ x x₃ x₄

Рис. 5.2.

Координаты исходных производственных помещений могут быть записаны как координаты соответствующих точек в виде (х_i, у_i), где i Є {1, 2, 3, 4}.

Координаты для нового склада, который предполагается спроектировать и разместить, можно положить равными (х, у). Очевидно, они служат переменными рассматриваемой задачи оптимизации, каждая из которых по своему характеру может принимать действительные значения.

В некоторой фиксированной прямоугольной системе координат значения переменных х, у могут быть как положительными, так и отрицательными. Задачу о размещении склада можно считать задачей оптимизации без ограничений.

В качестве целевой функции данной задачи будем рассматривать сумму расстояний от искомой точки (х, у) до каждой из заданных точек (х_i, у_i), где i Є {1, 2, 3, 4}.

Расстояние от i-го помещения до склада определяется по формуле:

, (5.1)

где .

Общее расстояние от всех четырех производственных помещений до склада будет определяться выражением:

(5.2)

Таким образом, математическая постановка задачи о размещении склада может быть записана в следующем виде:

, (5.3)

где R – область значений для х и у.

Поскольку целевая функция данной задачи является нелинейной, задача о строительстве склада относится к классу задач нелинейного программирования без ограничений.

Решение задачи о местоположении объекта с помощью MS EXCEL

Для решения данной задачи создать новый лист. Переименовать его в «Задача о размещении нового склада». Выполнить подготовительный этап для решения - создать макет листа (рис. 5.3).

Рис. 5.3.

С помощью процедуры поиска решения найти оптимальное значение формулы, содержащейся в целевой ячейке. Эта процедура работает с группой ячеек, связанных с формулой в целевой ячейке.

В ячейку G12 поместить значение целевой функции. Формула для ее вычисления: =СУММ(B7:B10).

В ячейку B7 будет ввести формулу:

=КОРЕНЬ(($B$12-B2)^2+($D$12-D2)^2).

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню Сервис – Поиск решения (рис. 5.4).

Рис. 5.4

В поле с именем Установить целевую ячейку ввести абсолютный адрес ячейки $G$12 – значение целевой функции, а в поле с именем Изменяя ячейки ввести абсолютный адрес ячеек $B$12:$D$12 (рис. 5.4). Поля с ограничениями можно оставить пустыми, поскольку целевая функция является выпуклой на всем множестве допустимых значений. Параметры поиска решения можно оставить без изменения (рис. 5.5).

Рис. 5.5

Параметры поиска решения задаются в каждом случае отдельно. Результат выполнения задачи о размещении склада вместе с графическим представлением показан на рис. 5.6.

Рис. 5.6

Замечание. Графическое представление размещения производственных помещений и нового склада выполнено с применением Мастера диаграмм (рис. 5.7). Для этого выделить предварительно массив данных, т.е. ячейки B14:C19. Затем выбирать тип диаграммы – Стандартные – Точечная (рис. 5.7), выполнить последовательно четыре шага Мастера диаграмм и получить готовую диаграмму решения задачи (см. рис. 5.6).

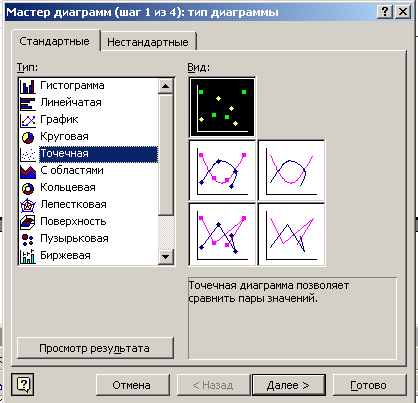
Рис. 5.7