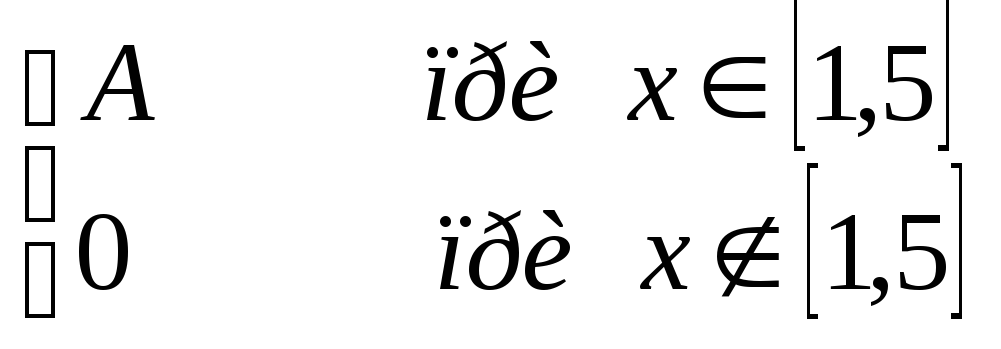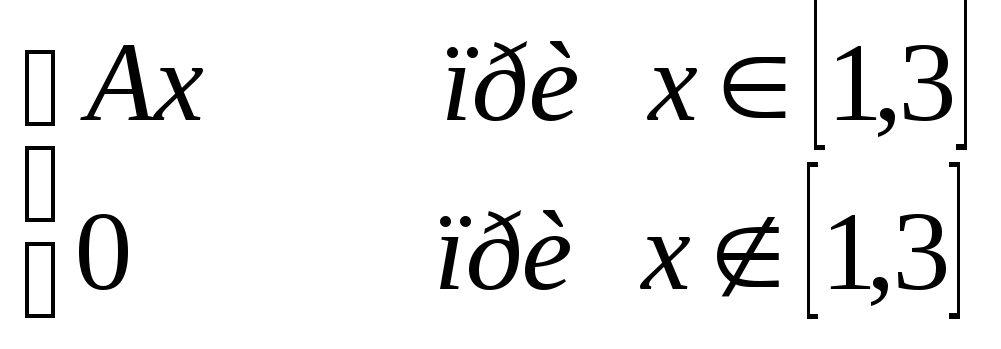Контрольная работа №6.

Задача 6. Нормальное распределение случайной величины.

Заданы математическое ожидание a и стандартное отклонение  нормально распределенной случайной величины X. Найти:

а) вероятность того, что случайная величина X примет значение, принадлежащее интервалу (,);

б) вероятность того, что абсолютная величина отклонения X – окажется меньше .

6.1. a=11  =3 =10 =13 =6

6.2. a=12  =4 =9 =14 =5

6.3. a=10  =2 =8 =15 =3

6.4. a=9  =5 =7 =12 =2

6.5. a=8  =6 =6 =11 =1

6.6. a=14  =3 =14 =17 =9

6.7. a=13  =7 =8 =13 =4

6.8. a=15  =8 =13 =20 =5

6.9. a=16  =5 =14 =19 =6

6.10. a=18  =4 =15 =20 =2

45

Задача 5. Непрерывная случайная величина.

Дана плотность распределения f(x) непрерывной случайной величины Х.

Найти:

1) постоянный параметр А;

2) функцию распределения F(x);

3) математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение (X);

4) вероятность попадания случайной величины X в интервал (,);

5) построить графики функций f(x) и F(x).

5.1.	f(x) =
5.2.	f(x) =
5.3.	f(x) =
5.4.	f(x) =
5.5.	f(x) =
5.6.	f(x) =

44

Ответ: m₀ = 12, р₃₀(12) = 0,1487.

Задача 5. Сколько нужно провести опытов, чтобы с вероятностью 0,901 утверждать, что частота интересующего нас события будет отличаться по абсолютной величине от вероятности появления этого события, равной 0,4, не более чем на 0,1?

Решение. По условию р = 0,4; q = 0,6;  = 0,1;

Воспользуемся формулой (4): 2 или



По таблице №2 Приложений значение аргумента х = 1,65. Следовательно, 0,204или,n = 65,42.

Таким образом, искомое число испытаний n = 66.

Ответ: n = 66.

4. Cлучайная величина Основные характеристики случайных величин

Определение 4. Случайной величиной Х называется величина, принимающая то или иное заранее неизвестное числовое значение в зависимости от исхода испытания.

Определение 5. Дискретной случайной величиной называется величина, которая может принимать только конечное или счетное множество значений, то есть такое множество, элементы которого можно пронумеровать.

Определение 6. Законом распределения дискретной случайной величины Х называется соответствие между возможными значениями Х и их вероятностями:

х	х1	х2	…	xn
p(х)	p(х1)	p(х2)	…	p(хn)

где .

Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание М(Х), дисперсия D(X) и среднее квадратическое отклонение (X).

М

13

атематическое ожидание дискретной случайной величины определяется соотношением:

М(Х) =.

Дисперсия дискретной случайной величины определяется соотношением:

.

Среднее квадратическое отклонение дискретной случайной величины определяется по формуле

.

С вероятностной точки зрения математическое ожидание случайной величины определяет среднее арифметическое значение, которое принимает случайная величина при очень большом числе испытаний.

Дисперсия же определяет среднее арифметическое квадратов отклонений случайной величины Х от ее математического ожидания при очень большом числе испытаний.

И дисперсия, и среднее квадратическое отклонение характеризуют степень рассеяния случайной величины Х в области ее математического ожидания.

Свойства математического ожидания:

1. М(С) = С, где С = const;

2. М(СХ) = СМ(Х);

3. М(Х  Y) = М(Х)  M(Y);

4. М(ХY) = М(Х)M(Y), если Х и Y – независимые случайные величины.

Свойства дисперсии:

1. D(C) = 0;

2. D(CX) = C²·D(X);

3. ;

4. D (Х  Y) = D(Х) + D(Y), если X и Y - независимые случайные величины.

Определение 7. Случайная величина называется непрерывной, если она может принимать все возможные значения из некоторого конечного или бесконечного интервала.

Определение 8. Интегральной функцией распределения случайной величины X называется функция, определяемая соотношением:

F(x) = p(X < x) =. (5)

Для дискретной случайной величины

F

14

(x) = p(X < x) =.

4.7.

X \Y	–4	–3	–1	0	1	3
1	0,03	0,04	0,06	0,02	0,02	0,03
2	0,07	0	0,07	0,03	0,05	0,03
3	0,04	0,04	0,05	0,05	0,03	0,05
4	0,06	0,07	0,06	0,06	0,02	0,02

a = –2, b = 3, C = 2

4.8.

X \Y	–8	–6	–4	–2	0	2
2	0,03	0,06	0,04	0,06	0,06	0,05
7	0,05	0,08	0,04	0	0,01	0,03
9	0,03	0,06	0,06	0,08	0,02	0,06
11	0,04	0	0,03	0,09	0,01	0,01

a = ,b = ,C = 9

4.9.

X \Y	–5	–3	–2	–1	0	1
3	0,01	0,04	0,11	0,06	0,05	0,04
7	0,02	0,06	0,13	0,02	0	0,01
8	0,08	0,05	0,03	0,03	0,02	0,03
10	0,09	0	0,03	0,02	0,03	0,04

a = 3, b = 2, C = 7

4.10.

X \Y	–4	–2	1	5	7	8
–2	0,06	0,02	0,1	0,02	0,05	0
–1	0,05	0	0,03	0,02	0,04	0,05
0	0,02	0,04	0,07	0,01	0,03	0,05
3	0,02	0,04	0,1	0,05	0,08	0,05

a = 2, b = 1, C = 0

43

4.3.

X \Y	–5	–3	–1	0	1	2
4	0,03	0,09	0,01	0,06	0,03	0,05
5	0,02	0,05	0,07	0,05	0,02	0,02
7	0,15	0,04	0,03	0,04	0,03	0,03
10	0	0,02	0,04	0,05	0,02	0,05

a = –1, b = 2, C = 5

4.4.

X \Y	3	4	6	7	8	9
–4	0,06	0,02	0,04	0,06	0,03	0,05
–2	0,04	0,07	0,03	0	0,05	0,03
1	0,06	0,04	0,09	0,06	0,03	0,02
2	0,07	0,03	0,05	0,06	0,01	0

a = 2, b = 3, C = 1

4.5.

X \Y	3	4	5	7	8	10
–5	0	0,06	0,03	0,03	0,04	0,02
–3	0,07	0,04	0,02	0,02	0,06	0,03
2	0,15	0,05	0,04	0,04	0,03	0,02
5	0,08	0,05	0,01	0,01	0,07	0,03

a = , b = , C = 2

4.6.

X \Y	1	2	3	4	5	6
–4	0,02	0,02	0,06	0,04	0,04	0,02
–3	0,03	0,01	0,04	0,08	0,03	0,07
–2	0,04	0,05	0,07	0,07	0,05	0,04
–1	0,01	0,02	0,03	0,06	0,03	0,07

a= 4, b = –2, C= –3

42

Интегральная функция распределения обладает следующими свойствами:

1) 0  F(x)  1, F(– ) = 0, F(+ ) = 0;

2) F(x) – неубывающая функция, т.е. F(x₁)  F(x₂) при x₁  x₂;

3) p(x₁ < X < x₂) = F(x₂) – F(x₁).

Определение 9. Дифференциальной функцией распределения f(x) или плотностью вероятности называется первая производная от интегральной функции распределения: f(x) = F (x). Понятие f(x) применимо только для непрерывных случайных величин.

Функция f(x) обладает следующими свойствами:

1) f(x)  0;

2) ; (6)

3) p(x₁  X  x₂) = .(7)

Математическое ожидание, дисперсия и среднее квадратическое отклонение непрерывной случайной величины определяются соотношениями:

Замечание. Если значения непрерывной случайной величины X заполняют некоторый интервал (a, b), т.е. f(x)  0при x  (a, b), f(x)  0при x  (a, b), тогда

Для вычисления дисперсии можно использовать формулу:

D(X) = М(Х ²) – М ²(Х).

Задача. Дана плотность распределения непрерывной случайной величины X. Найти:

1. постоянный параметр A;

2. функцию распределения F(x);

3. математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение ;

4. вероятность попадания случайной величины X в интервал (1; 4);

5. п

   15

   остроить графики функцийf(x) и F(x).

Решение. Распишем функцию плотности распределения следующим образом:

1. Постоянный параметр A находится из условия (6). С учетом областей изменения аргумента x с различным аналитическим заданием f(x) имеем:

Поскольку подынтегральная функция в двух крайних интегралах суммы тождественно равна 0, то равны 0 и сами эти интегралы. В силу этого:

2. Интегральный закон распределения находим согласно (5) также с учетом областей изменения аргумента х с различным аналитическим заданием f(x).

Для х < 0: в этой области значенийх.

Для 0  x  3:

Для х > 3:

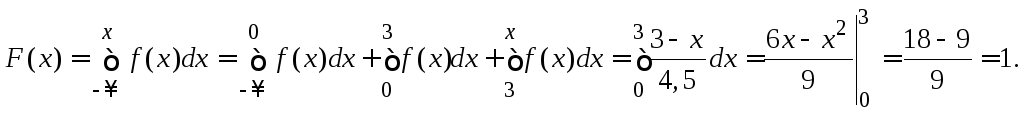
Таким образом,

16

3.10. Агрегат содержит 5000 деталей. Вероятность отказа детали за время работы агрегата равна 0,001. Найти вероятность того, что за время работы агрегата откажет более чем одна деталь.

Задача 4. Двумерная дискретная случайная величина.

Дана дискретная двумерная случайная величина (X,Y). Найти:

1) безусловные законы распределения компонент Х и Y;

2) математические ожидания составляющих компонент М(Х), M(Y) и центр рассеяния R₀ = {M(X), M(Y)}; ковариацию компонент cov(X, Y);

3) условный закон распределения X при Y = C и найти M(X / Y = C);

4) закон распределения случайной величины Т = аХ + b, математическое ожидание М(Т) и дисперсию D(T);

5) закон распределения случайной величины Z = Х + Y; математическое ожидание M(Z) и дисперсию D(Z);

6) построить график интегральной функции распределения F(z) случайной величины Z.

4.1.

X \Y	–7	–3	0	1	2	4
–2	0,08	0,1	0,05	0,02	0,03	0,13
–1	0,01	0,05	0,06	0,03	0,05	0,04
0	0	0,1	0,07	0,03	0,01	0,02
3	0,01	0,05	0,02	0,02	0,01	0,01

a = 2, b = –1, C = 0

4.2.

X \Y	1	2	4	5	7	8
–3	0,01	0,05	0,05	0,06	0	0,03
–2	0,07	0,1	0,05	0,03	0,02	0,08
–1	0,04	0,04	0,05	0,04	0,02	0,03
0	0,03	0,06	0,05	0,02	0,01	0,06

a = 3, b = 1, C = –1

41

принадлежит он к двум 1-ым или 3-ем последним?

2.10. Известно, что 5% всех мужчин и 0,25% всех женщин дальтоники. Считая, что всех мужчин и женщин одинаковое количество, найти вероятность того, что случайно выбранное лицо окажется дальтоником. Пусть наугад выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина?

Задача 3. Схема Бернулли.

3.1 Отношение грузовых и легковых автомобилей, подъезжающих к автозаправочной станции для заправки, 2 : 3. Найти вероятность того, что из 100 очередных машин к автозаправочной станции подъедут 60 легковых.

3.2. Книга издана тиражом 20000 экземпляров. Вероятность того, что в книге имеется дефект брошюровки, равна 0,0002. Найти вероятность того, что тираж содержит 5 неправильно сброшюрованных книг.

3.3 Вероятность полной заполняемости каждого из 60 санаториев города-курорта в осенний период равна 0,64. Найти вероятность того, что в октябре с полной нагрузкой будут работать более 30 санаториев.

3.4. Коэффициент использования каждого из 7 станков равен 0,8. Найти вероятность того, что в данный момент работают 4 станка.

3.5. На склад поступили телевизоры, 90 % которых исправны. Сколько телевизоров надо взять со склада наудачу, чтобы с вероятностью 0,993 утверждать, что частость исправных телевизоров среди взятых находится между 0,85 и 0,95?

3.6. Вероятность того, что деталь не прошла проверку ОТК, равна 0,1. Найти вероятность того, что среди 120 случайно отобранных деталей окажутся непроверенными от 10 до 20 деталей.

3.7. На склад поступило 400 изделий. Вероятность того, что изделие высшего сорта, равна 0,8. Найти вероятность того, что на складе число изделий высшего сорта от 290 до 330.

3.8. Автоматический станок изготавливает 3/5 числа деталей первого сорта и 2/5 – второго сорта. Определить вероятность наивероятнейшего числа деталей первого сорта среди отобранных 54 деталей.

3.9. На каждую из 144 купленных акций различных акционерных обществ и компаний их владелец за год получает дивиденды с вероятностью 0,64. Найти вероятность того, что относительная частота акций, которые в следующем году принесут дивиденды, отклонится по абсолютной величине от вероятности 0,64 не более чем на 0,05 в условиях стабильной котировки акций.

40

3. Найдем математическое ожидание

Найдем дисперсию

Тогда .

4) Найдем вероятность попадания случайной величины Х в интервал (1; 4) по формуле (7):

,

так как х = 4 принадлежит третьей области изменения х, а значение функции в этой области равно 1; х = 1 принадлежит второй области изменения аргумента х, а значение функции в этой области рассчитывается при подстановке данного аргумента х в выражение

5) Используя полученные функции f(x) и F(x), строим их графики

f(x) F(x)

1 1

2/3

0,5 0,5

x x

–1 0 1 2 3 4 –1 0 1 2 3 4

Рис. 1. Рис. 2.

17