Инфа

∙нет правильных вариантов ответов

∙не является практически применяемым методом

∙являетя предельно точным и применяется на практике для проведения конечных

расчетов

∙является сравнительно грубым и применяется на практике в основном для

проведения ориентировочных расчетов

В общем виде ОДУ можно представить следующим образом

∙

∙

∙

∙

Начальными условиями ОДУ n-го порядка являются (для n=2)

∙x0, y0, y'0

∙x0, y0, y'0, y"0

∙x0, y'0

∙нет верного ответа

Из курса высшей математики известно множество аналитических методов, позволяющих найти решения ДУ. Однако, в некоторых случаях, например, если функции или коэффициенты ДУ представляют собой таблицу экспериментально полученных данных, использование аналитических методов

∙возможно, но не обязательно

∙невозможно

∙необходимо

∙упрощает решение

Погрешность метода Эйлера при решения ОДУ связана с величиной шага интегрирования отношением 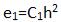, где -

∙нет правильных вариантов ответов

∙произвольная постоянная

∙зависимая переменная

∙односложная функция

Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании

∙трех предыдущих значений функции

∙одного предыдущего значения функции

∙двух предыдущих значений функции

∙всех предыдущих значений функции

Погрешность методов Рунге-Кутты 4-го порядка для решения ОДУ пропорциональна величине

∙

∙

∙

∙

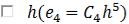
Вформуле оценки погрешности при использовании метода автоматического выбора шага порядок используемого метода Рунге-Кутты при решения ОДУ

∙учитывается с помощью коэффициента, равного порядку метода

∙в списке нет правильного ответа

∙учитывается в расчетных формулах используемого метода

∙не учитывается

Для применения формул Рунге-Кутты при решении ОДУ первого порядка к уравнениям n-го порядка

∙находят значение при 0 параметре

∙уравнение приводятся к системе из n уравнений первого порядка

∙нет правильных вариантов

∙находят его производную

Цель двойного просчёта при решении ОДУ состоит в том, чтобы в каждой точке решения значения погрешности

∙равнялись 0

∙отличались на величину, больше погрешности

∙отличались на величину, не превышающую заданную величину погрешности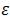

∙нет правильного ответа

Погрешность метода Рунге-Кутты четвёртого порядка для решения ОДУ

∙равна погрешности методов 1-го и 2го

∙нулевая

∙меньше, чем методов 1-го и 2-го

∙больше погрешности методов 1-го и 2-го

Метод решения ОДУ, в котором подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников, это

∙метод Эйлера

∙метод Рунге-Кутты 4-го порядка

∙модифицированный метод Эйлера

∙метод Рунге-Кутты 3-го порядка

Требуемая точность решения ОДУ достигается применением в расчетах метода

∙Эйлера

∙автоматического выбора шага

∙аналитического выбора шага

∙золотого сечения

Если 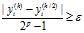, то для решения ОДУ

∙шаг уменьшается вчетверо и продолжается уточнение yi в точке xi

∙шаг увеличивается вдвое и продолжается уточнение yi в точке xi

∙шаг увеличивается вчетверо и продолжается уточнение yi в точке xi

∙шаг уменьшается вдвое и продолжается уточнение yi в точке xi

Порядок методов Рунге-Кутты при решения ОДУ определяется

∙количеством переменных в дифференциальном уравнении

∙количеством производных в дифференциальном уравнении

∙количеством оставленных членов ряда при разложении функции в ряд Тейлора

∙в списке нет правильного ответа

Кначальным условиям при решении ОДУ 1-го порядка численными методами относятся

∙в списке нет правильного ответа

∙

∙

∙

Обыкновенное дифференциальное уравнение это

∙дифференциальное уравнение первого порядка

∙в списке нет правильного ответа

∙дифференциальное уравнение n-ого порядка

∙дифференциальное уравнение от одной переменной

Любое физическое явление, в котором рассматривается степень изменения одной переменной по отношению к другой переменной, математически описывается

∙логарифмической системой

∙интерполяционной схемой

∙переменной функцией

∙дифференциальным уравнением

Метод решения ОДУ, в котором подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников, это

∙метод Рунге-Кутты 3-го порядка

∙метод Эйлера

∙метод Рунге-Кутты 4-го порядка

∙модифицированный метод Эйлера

Методы Рунге-Кутты решения дифференциальных уравнений являются

∙трехшаговыми методами

∙в списке нет правильного ответа

∙одношаговыми методами

∙двухшаговыми методами

Процесс решения дифференциального уравнения называется

∙интегрированием

∙интерполированием

∙дифференцированием

∙в списке нет правильного ответа

для увеличения точности решения ОДУ количество итераций в методе автоматического выбора шага

∙увеличивается

∙уменьшается

∙накапливается

∙не меняется

При решении ОДУ по сравнению с методом Эйлера, метод «прогноза и коррекции»

∙имеет большую погрешность

∙не имеет разницы

∙требует меньшее количество итераций для обеспечения заданной точности

∙требует большее количество итераций для обеспечения заданной точности

Аналитическое решение ОДУ 1-го порядка это

∙

∙таблица значений искомой функции

∙в списке нет правильного ответа

∙функция y(x), которая при подстановке в уравнение обращает его в тождество

Наиболее популярными среди классических одношаговых методов решения ОДУ являются методы Рунге-Кутты

∙третьего порядка

∙первого порядка

∙второго порядка>

∙четвертого порядка>

Методы Рунге-Кутты при решения ОДУ называют одношаговыми методами, потому что

∙решение ОДУ находят за один шаг

∙в списке нет правильного ответа

∙для вычисления очередной точки решения используются сведения только о предыдущей точке

Численным решением ОДУ 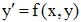является

∙

∙в списке нет правильного ответа

∙

∙таблица значений искомой функции

общая формула для оценки погрешности решения ОДУ методами Рунге-Кутты имеет вид

∙

∙

∙

∙

Методы Рунге-Кутты решения дифференциальных уравнений являются

∙двухшаговыми методами

∙в списке нет правильного ответа

∙одношаговыми методами

∙трехшаговыми методами

∙

вметоде Эйлера для нахождения интеграла используется метод

∙левых прямоугольников

∙трапеций

∙золотого сечения

∙нет верных вариантов

- эта формула является формулой для определения очередного значения функции по методу

∙Рунге-Кутты 1-го порядка

∙Рунге-Кутты 2-го порядка

∙Рунге-Кутты 4-го порядка

∙в списке нет правильного ответа

Метод решения обыкновенного дифференциального уравнения, при котором подынтегральная функция на отрезке [xi;xi+1] аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом трапеции, это

∙в списке нет правильного ответа

∙метод Рунге-Кутты третьего порядка

∙все перечисленные

∙исправленный или модифицированный метод Эйлера

∙метод Эйлера или Рунге-Кутты первого порядка

Вмодифицированном методе Эйлера для решения ОДУ на каждом шаге 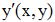необходимо вычислять

∙три раза

∙четыре раза

∙два раза

∙один раз

Метод решения ОДУ, в котором подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников, это

∙метод Эйлера

∙метод Рунге-Кутты 4-го порядка

∙метод Рунге-Кутты 3-го порядка

∙модифицированный метод Эйлера

При решении ОДУ методом «прогноза и коррекции» порядок точности

∙второй

∙четвёртый

∙третий

∙первый

Обыкновенное дифференциальное уравнение это

∙в списке нет правильного ответа

∙дифференциальное уравнение от одной переменной

∙дифференциальное уравнение n-ого порядка

∙дифференциальное уравнение первого порядка

Применение переменного шага для решения ОДУ является

∙возможным только в методе Рунге-Кутты 4-го порядка

∙невозможным в методах Рунге-Кутты

∙возможным только в методе Эйлера

∙возможным во всех методах Рунге-Кутты

Решить ОДУ n-го порядка

∙можно, сведя к ОДУ 1-го порядка

∙нельзя

∙можно, последовательно удаляя из уравнения производные высших порядков

∙можно, перейдя к системе ОДУ 1-го порядка

Метод Эйлера называют методом Рунге-Кутты первого порядка при решения ОДУ, потому что

∙в качестве начальных условий требуется одна точка решения

∙для получения очередной точки проводится одно уточнение

∙методом Эйлера решается ОДУ первого порядка

∙в формуле Эйлера одна производная

Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании

∙трех предыдущих значений функции

∙одного предыдущего значения функции

∙всех предыдущих значений функции

∙двух предыдущих значений функции

Если 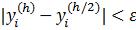, то шаг для следующей точки для решения ОДУ

∙выбирается равным h

∙выбирается равным h/2

∙не выбирается

∙выбирается равным h/4

Отрезком неопределённости называется отрезок, на котором

∙локализован единственный минимум

∙находятся несколько локальных минимумов

∙локализован единственный максимум

Группа методов многомерной оптимизации, в которых точка минимума (максимума) функции находится путем вложенных отрезков, называется

∙ методом спуска

∙методом штрафных функций

∙методом одномерной оптимизации

∙в списке нет правильного ответа

Правильной записью приближенного числа является

∙

∙

∙

∙

Приведение уравнения к виду, удобному для итераций, означает

∙	замена				уравнением

∙замена равносильным

∙замена уравнением

∙в списке нет правильного ответа

Этапы решения нелинейного уравнения называются

∙вычисления каждого из корней уравнения

∙отделение корней и уточнение отделенного корня

∙графическое и аналитическое вычисления корня

∙табличное отделение корня и аналитическое уточнение корня

Корень x на отрезке [a;b] существует, если

∙f(x) на концах отрезка имеет разные знаки

∙первая производная f(x) существует и сохраняет знак на данном отрезке

∙вторая производная f(x) положительна

∙первая производная f(x) положительна

На отрезке [a;b] имеется хотя бы один корень, если

∙

∙

∙

∙

Этап отделения корней нелинейного уравнения необходим, потому что

∙для уточнения корня потребуется слишком много итераций

∙уравнение может иметь несколько корней

∙в списке нет правильного ответ

∙метод уточнения корня разойдется

Этап «отделения корней» нелинейного уравнения заключается в

∙нахождении отрезков, внутри которых находится строго один корень

∙нахождении значения корня с заданной точностью

∙нахождении отрезка, для которого выполняется условие

∙отделении корня с заданной точностью

Метод решения нелинейного уравнения, обладающий свойством "самокоррекции"

∙метод хорд

∙метод итераций

∙метод половинного деления

∙метод Ньютона

При вычислении погрешности результата, полученного при умножении приближенных чисел друг на друга,

∙их относительные погрешности перемножаются

∙их относительные погрешности делятся

∙их относительные погрешности вычитаются

∙их относительные погрешности складываются

Чтобы повысить точность результата вычислений численными методами, надо

∙увеличить количество итераций

∙уменьшить величину заданной погрешности результата

∙в списке нет правильного ответа

∙увеличить величину заданной погрешности результата