Инфа

В методе наискорейшего спуска (НС) при решении задачи многомерной оптимизации на каждой итерации шаг выбирается исходя из условия

∙максимума целевой функции

∙минимума целевой функции

∙равенства нулю целевой функции

∙в списке нет правильного ответа

Для представления чисел в памяти компьютера применяют два способа: с фиксированной запятой

и

∙с нефиксированной запятой

∙в виде целого числа

∙в виде дробной части числа

∙с плавающей запятой

Степень отличия приближенного числа от его точного значения - это

∙приближение

∙удаление

∙погрешность

∙разность

Числа, представленные в ПК как тип Single или Double относятся к классу

∙натуральных

∙дробных

∙целых

∙Long

Относительная точность представления вещественных чисел одинакова в любой части диапазона

изависит лишь от числа разрядов

∙отводимых под порядок числа

∙отводимых под мантиссу числа

∙отводимых под знак порядка числа

∙отводимых под целую часть числа

Дробь 1/3 в десятичной системе получится

∙периодической

∙такой же

∙бесконечной

∙конечной

Абсолютная погрешность суммы приближенных чисел 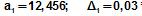; ; 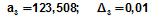равна

∙

∙

∙

Погрешность, связанная с описанием математической моделью реального явления, это

∙погрешность округления

∙в списке нет правильного ответа

∙погрешность метода

∙погрешность задачи

Модуль разности между точным и приближенным значением это

∙относительная погрешность

∙абсолютная погрешность

∙точность

∙в списке нет правильного ответа

Абсолютная погрешность числа измеряется

∙в тех же единицах измерения, что и само число

∙в процентах

∙в долях

∙это безразмерная величина

Всякий глобальный минимум выпуклой функции является одновременно и

∙точкой перегиба

∙максимумом

∙нет правильного ответа

∙локальным

Формат чисел с плавающей запятой является международным стандартом представления

∙натуральных чисел

∙целых чисел

∙дробных чисел

∙только бесконечных дробей

Относительная погрешность выражается отношением

∙абсолютной погрешности к модулю разности приближенного и точного чисел

∙абсолютной погрешности к модулю приближенного значения

∙в списке нет правильного ответа

∙модуля приближенного числа к абсолютной погрешности

Относительная погрешность числа измеряется

∙это безразмерная величина

∙в процентах

∙в тех же единицах измерения, что и само число

∙в процентах или долях

Точность вещественного числа в ПК определяется

∙количеством цифр в этом числе

∙длиной числа

∙знаком числа

∙экспонентой

Воснове представления чисел с плавающей запятой лежит экспоненциальная форма записи

∙

∙

∙

∙

Относительная погрешность выражается отношением

∙абсолютной погрешности к модулю приближенного значения

∙абсолютной погрешности к модулю разности приближенного и точного чисел

∙в списке нет правильного ответа

∙модуля приближенного числа к абсолютной погрешности

погрешность, связанная с описанием математической моделью реального явления, это

∙погрешность округления

∙в списке нет правильного ответа

∙погрешность задачи

∙погрешность метода

Погрешность, обусловленная выполнением действий над данными, полученными с ограниченной точностью, это

∙неустранимая погрешность

∙погрешность округления

∙погрешность метода

∙в списке нет правильного ответа

Потери точности при записи десятичных дробей велики из-за того, что

∙происходит округление дробей

∙двоичный эквивалент числа получается с погрешностями

∙двоичная дробь впоследствии приводится к нормализованному виду

∙в компьютере числа хранятся в двоичной системе

Для увеличения точности решения ОДУ количество итераций в методе автоматического выбора шага

∙уменьшается

∙накапливается

∙не меняется

∙увеличивается

Функция на отрезке унимодальная, если

∙в списке нет правильного ответа

∙на выбранном отрезке функция имеет два минимума

∙на выбранном отрезке функция имеет один экстремум

∙на выбранном отрезке функция не имеет ни одного минимума

При решении задачи многомерной оптимизации для функции F(x,y) = 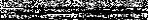, функция Ф(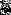) будет следующей

∙Ф() =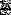

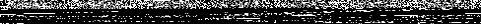
∙Ф() =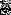

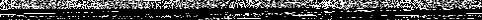
∙Ф() =

Из перечисленных понятий к методам многомерной оптимизации относится

∙метод Гаусса

∙метод Сильвестра

∙метод покоординатного спуска

∙правило Рунге

Величина шага на каждой итерации в методе наискорейшего спуска при решении задачи многомерной оптимизации определяется из условия

∙постоянства функции

∙минимума функции

∙максимума функции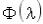

∙в списке нет правильного ответа

Абсолютная погрешность суммы приближенных чисел ; ; 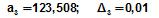равна

∙

∙

∙

Формула для определения абсолютной погрешности числа это

∙

∙

∙

∙

Отличие численного метода наискорейшего спуска при решении задачи многомерной оптимизации состоит в том, что поиск значения на каждой итерации происходит

∙аналитическим методом

∙методом конфигураций

∙методом штрафных функций

∙одним из численных методов одномерной оптимизации

Градиентные методы – это методы, в которых движение к точке минимума совпадает с направлением

∙в списке нет правильного ответа

∙одной из координат осей

∙вектора градиента функции

∙вектора антиградиента функции

Вметоде наискорейшего спуска (НС) при решении задачи многомерной оптимизации на каждой итерации шаг выбирается исходя из условия

∙максимума целевой функции

∙равенства нулю целевой функции

∙в списке нет правильного ответа

∙минимума целевой функции

Погрешность численного решения задачи определяется

∙чувствительностью вычислительного алгоритма к погрешностям округления

∙погрешностью представления вещественных чисел в компьютере

∙значением исходных данных

∙обусловленностью решаемой задачи

Роль погрешности в численных методах

∙останавливает процесс вычислений

∙тормозит процесс вычислений

∙никакой

∙ускоряет процесс вычислений

Точными числами являются

∙

∙ 13

∙43.45

∙0.0001

К точным числам относятся

∙натуральные

∙действительные

∙приближенные

∙дробные

Абсолютная точность представления вещественных чисел с фиксированной запятой

∙одинакова в любой части диапазона

∙постоянна

∙равна нулю

∙различна в каждой части диапазона

Если говорят, что расчеты проведены с точностью 0.01, это означает, что

∙предельная абсолютная погрешность равна 0.01

∙предельная относительная погрешность равна 0.01

∙максимальное значение погрешности равно 0.01

∙погрешность округления равна 0.01

Вградиентном методе с дроблением шага (ГДШ) при решении задачи многомерной оптимизации на каждой итерации шаг

∙уменьшается в 2 раза

∙увеличивается в 3 раза

∙увеличивается в 2 раза

∙уменьшается в 3 раза

Тестовые задачи по теме « Интерполяция функций»

Тесты 1-го блока сложности

30. При построении линейного интерполяционного многочлена Лагранжа L1 ( x) значение функции, заданной таблично, значение функции в точке х=0.18, равно…

х	0,1	0,15	0,2
у	-1	-0,7	-0,5

5)L1 (0.18) = -0.58; *

6)L1 (0.18) = -0.48;

7)L1 (0.18) = 0.68;

8)Формулу Лагранжа использовать нельзя.

31.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=0,18…

х	0,1	0,2	0,3
у	0,8	0,5	0,6

5)P1 (0.18) = 0.77; *

6)P1 (0.18) = -0.752;

7)P1 (0.18) = 0.568;

8)Формулу Ньютона использовать нельзя.

32.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=1.8 равно…

х	1	2	3
у	2,2	5,2	8,4

1)P1 (0.18) = 4.6; *

2)P1 (0.18) = -0.752;

3)P1 (0.18) = 1.568;

4)Формулу Ньютона использовать нельзя.

33.При построении линейного интерполяционного многочлена Лагранжа L1 ( x) для функции, заданной таблично, значение в точке х=4,6 равно …

х	3	4	5
у	5,2	8,4	10,5

1)L1 (4.6) = 9.66; *

2)L1 (4.6) = 8.654;

3)L1 (4.6) = 7.561;

4)L1 (4.6) = 4.675.

34.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=4,2 равно…

х	4	4.5	5
у	5,3	8,2	11,4

1)P1 (4.2) = 6.46; *

2)P1 (4.2) = 8.752;

3)P1 (4.2) = 9.568;

4)P1 (4.2) = 6.3.

35.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=1.36 равно…

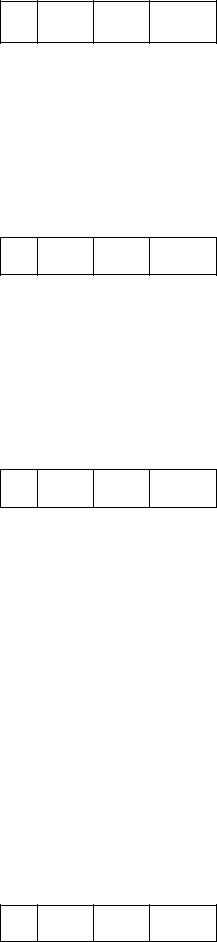
х	1.2	1.3	1.4
у	6,2	3,4	5,5

1)P1 (1.36) = 4.66; *

2)P1 (1.36) = 6.75;

3)P1 (1.36) = 10.58;

4)Формулу Ньютона использовать нельзя.

36.При построении линейного интерполяционного многочлена Лагранжа L1 ( x) для функции, заданной таблично, значение функции в точке х=6,9 равно…

х	6	7	8
у	12.0	16.6	14.0

1)L1 (6.9) = 16.14; *

2)L1 (6.9) = 10.654;

3)L1 (6.9) = 12.61;

4)L1 (6.9) = 14.16.

37.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=3,6 равно…

х	2	3	4
У	6,5	7,0	9,5

1)P1 (3.6) = 8.5; *

2)P1 (3.6) = 6.75;

3)P1 (3.6) = 10.58;

4)P1 (3.6) = 7.12.

38.При построении линейного интерполяционного многочлена Лагранжа L1 ( x) для функции, заданной таблично, значение функции в точке х=2,6 равно…

х	2.5	3	4
у	13	26	43

1)L1 (2.6) = 15.6; *

2)L1 (2.6) = 13.64;

3)L1 (2.6) = 12.61;

4)L1 (2.6) = 24.16.

39.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=3,25 равно…

x	3	4	5
f(x)	5,2	8,4	10,5

1) P1 (3.25) = 6.0; *

2)P1 (3.6) = 6.75;

3)P1 (3.6) = 10.58;

4)P1 (3.6) = 7.12.

40.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=1,4 равно…

x	1	2	3
f(x)	2,2	5,2	8,4

1)P1 (1.4) = 3.4; *

2)P1 (1.4) = 2.75;

3)P1 (1.4) = 6.58;

4)P1 (1.4) = 7.12.

41.При построении линейного интерполяционного многочлена Лагранжа L1 ( x) для функции, заданной таблично, значение функции в точке х=2,5 равно…

x	0	2	4
f(x)	1,7	1,9	2,5

5)L1 (2.5) = 2.05; *

6)L1 (2.5) = 2.99;

7)L1 (2.5) = 3.61;

8)L1 (2.5) = 4.16.

42.При построении линейного интерполяционного многочлена Лагранжа L1 ( x) для функции, заданной таблично, значение функции в точке х=0,25 равно…

x	0.2	0.3	0.6
f(x)	4,5	5,0	7.6

5)L1 (0,25) = 4.75; *

6)L1 (0,25) = 1.00;

7)L1 (0,25) = 5.61;

8)L1 (0,25) = 6.16.

43.При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=0,41 равно…

x	0.4	0.5	0.6
f(x)	0,6	0,55	0.65

5)P1 (0.41) = 0.575; *

6)P1 (0.41) = 1.75;

7)P1 (0.41) = 0.58;