1. Числовые множества. Мощность множеств. Точные верхняя и нижняя границы множества.

1. Натуральные числа.

Числа 0, 1, 2, 3, 4,… называются натуральными.

Множество всех натуральных чисел обозначается символом N. Принадлежность числа a к множеству натуральных чисел обозначается так a ∈ N.

2. Целые числа.

Множество целых чисел состоит из всех натуральных чисел взятых со знаками плюс и минус.

То есть целыми числами являются все числа 0, 1, 2, 3, 4,… и -1, -2, -3, -4,…. Множество целых чисел обозначается символом P.

Замечание.

Любое число входящее в множество N входит и во множество P.

В таких случаях говорят что множество N является подмножеством множества P, и обозначают так N ⊆ P.

3. Рациональные числа.

Соотношение двух целых чисел называется рациональным числом, то есть числа вида (a ∈ P, b ∈ P, b ≠ 0). Множество всех рациональных чисел обозначается символом R.

Любое целое число c  будет также и рациональным числом, потому что , поэтомуP ⊆ R.

4. Иррациональные числа.

Иррациональным числом называется числа вида π = 3,141592… или = 1,41… , то есть это такие числа у которых дробная часть представляет бесконечную не периодическую дробь.

Множество всех иррациональных чисел обозначается символом Q.

5. Вещественные числа.

Вещественные числа это все вышеперечисленные числа, то есть это все натуральные числа, все целые числа, все рациональные и иррациональные числа. Множество всех вещественных чисел обозначается символом Z.

Мощность множества — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

В основе этого понятия лежат естественные представления о сравнении множеств:

1. Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность).

2. Обратно: множества, равные по мощности, должны допускать такое взаимно-однозначное соответствие.

3. Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

Определение. Множество Х называется ограниченным сверху (снизу), если существует число «с» такое, что для любого 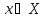выполняется неравенство.

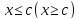Свойство точной верхней (нижней) грани. Как бы мало ни было число 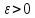, существует число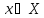такое, что.

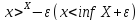Теорема. Любое непустое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.

2. Предел последовательности

Определение. Число а называется пределом последовательности 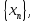если для любого положительного числа ε существует номерN такой, что при n>N выполняется неравенство

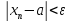
При этом последовательность 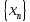называетсясходящейся, в противоположном случае - расходящейся.

3. Теорема о зажатой последовательности

Теорема. Если даны три последовательности {X_n}, {Y_n}, {Z_n} причём lim Х_n=lim Z_n=b и для всех n выполняется неравенство X_nY_nZ_n то и последовательность Y_n тоже имеет предел, равный b.

4. Теорема о сходимости монотонной последовательности

Теорема. Если неубывающая (невозрастающая) последовательность {X_n} ограничена сверху (снизу), то она сходится.

5. Бесконечно малые и бесконечно большие величины

Определение 1. Последовательность {x_n} называется бесконечно большой, если для любого положительного числа А существует номер N такой, что при n>N выполняется неравенство |x_n|>A.

Определение 2. Последовательность {α_n} называется бесконечно малой, если для любого положительного числа ε существует номер N такой, что при n>N выполняется неравенство .

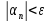Теорема. Если {x_n} – бесконечно большая после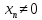довательность, , то последовательность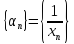бесконечно малая, и, обратно, если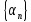– бесконечно малая последовательность,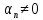, то последовательностьбесконечно большая.

6. Свойства бесконечно малых

Функция α(х) называется бесконечно малой при , если, т. е. для любого числа ε > 0 существует такое число δ > 0, что для всехх, удовлетворяющих неравенству , выполняется неравенство. 

Свойства бесконечно малых.