
- •1. Натуральные числа.
- •1. Если функции иявляются бесконечно малыми, то функциятакже есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
- •2. Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая.
- •3. Произведение постоянной на бесконечно малую есть бесконечно малая.
- •4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
- •8. Первый замечательный предел. Второй замечательный предел
- •9. Критерий Коши сходимости последовательности
- •10. Предел функции, два определения.
- •12. Непрерывность функции. Разрывы первого и второго рода
- •13. Теоремы Вейерштрасса о функции непрерывной на отрезке.
- •14. Теорема о свойстве непрерывной на отрезке функции принимающей на концах отрезка значения разных знаков (Больцано-Коши).
- •15. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины.
- •16. Сравнение бесконечно больших величин. Эквивалентные бесконечно большие величины.
- •17.Применение эквивалентных бесконечно малых и бесконечно больших величин для вычисления пределов.
- •18 Производная функции. Механический и геометрический смысл производной.
- •Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •19 Свойства производных. Правила дифференцирования
- •20 Производные элементарных функций.
- •21 Производная сложной функции. Производная обратной функции
- •22 Дифференциал функции. Геометрический смысл
- •23 Приближенное выражение приращения функции через дифференциал.
- •24 Производная высшего порядка.
- •Формула Тейлора
- •34. Асимптоты
- •35. Выпуклость и вогнутость графика функции. Точки перегиба
- •43.Замена переменной и интегрирование по частям в определенном интеграле.
- •44.Приложение интегралов. Площадь плоской фигуры.
- •45.Несобственные интегралы 1-го и 2-го рода. Сходимость интегралов.
- •51.Предел последовательности n-мерных точек.
- •52. Предел функции многих переменных, два определения.
- •В этом случае пишут илипри.
- •53. Непрерывные функции многих переменных.
- •54. Частные производные первого порядка.
- •60. Градиент функции, свойства градиента
- •63. Необходимые условия локального экстремума дифференцируемой функции многих переменных. Стационарные точки.
- •64. Достаточное условие экстремума функции многих переменных.
- •65. Комплексные числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Эйлера. Вычисление корней многочленов.
- •66. Дифференциальные уравнения, основные понятия.
- •67. Дифференциальные уравнения с разделяющимися переменными.
- •68. Линейные уравнения первого порядка.
- •69. Линейные дифференциальные уравнения с постоянными коэффициентами второго порядка.
45.Несобственные интегралы 1-го и 2-го рода. Сходимость интегралов.
Несобственный интеграл 1-го рода.
Определение.
Пусть функция f
( x)
определена при x≥a
и имеет определенные интегралы
 при∀b>a
. Эти интегралы называются частными.
Если существует конечный предел
при∀b>a
. Эти интегралы называются частными.
Если существует конечный предел
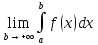 ,
то он называется несобственным интегралом
1-го рода и обозначается
,
то он называется несобственным интегралом
1-го рода и обозначается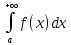 ,
при этом говорят, что интеграл сходится.
В противном случае – расходится.
,
при этом говорят, что интеграл сходится.
В противном случае – расходится.
Несобственный интеграл 2-го рода.
Определение.
Пусть функция f
(x)
определена на полуинтервале [a
,b)
и не ограничена вблизи точки b, которую
в этом случае будем называть особой.
Пусть для любого
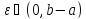 существуют определенные интегралы
существуют определенные интегралы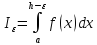 ,
которые будем называть частными
интегралами. Если существует конечный
предел
,
которые будем называть частными
интегралами. Если существует конечный
предел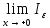 ,
то он называется несобственным интегралом
2-го рода и обозначается
,
то он называется несобственным интегралом
2-го рода и обозначается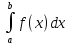 .
.
Несобственные интегралы 1-го и 2-го рода . Сходимость интегралов.


Абсолютная и условная сходимости несобственного интеграла.

Числовые ряды, основные понятия, сходимость ряда. Общие признаки сходимости ряда.

Свойства сходящихся рядов. Действия с рядами.
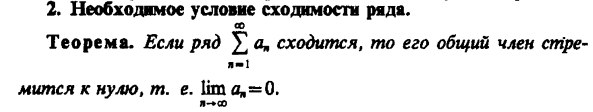
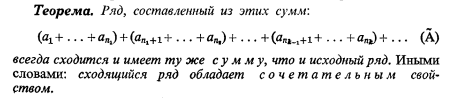
Ряды с неотрицательными членами. Теоремы сравнения рядов. Признаки сходимости положительных рядов.



Арифметическое n-мерное пространство. Расстояние между точками пространства. Открытый и замкнутый шар в n-мерном пространстве.
Множество всех упорядоченных совокупностей по n чисел (х1,х2,...,хn) называется арифметическим n-мерным пространством (Rn)
(n - размерность пространства).
Совокупность
точек n-мерного пространства, для которых
определено расстояние по формуле (1.1),
называется n-мерным Евклидовым
пространством.
![]()
Свойства расстояния между двумя точками:
1. r(А,В) ³ 0, причем если r(А,В) = 0, следовательно, А = В.
2. r(А,В) = r(В,А) для всех точек А, В Î Rn,
3. r(А,C) £ r(A,В) + r(B,C) для всех точек А, В, C Î Rn,
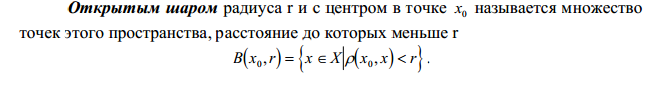

51.Предел последовательности n-мерных точек.

![]()
52. Предел функции многих переменных, два определения.
а)
Определение предела по Коши.
Число А называется пределом функции
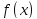 в точке
в точке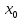 ,
если эта функция определена в некоторой
окрестности точки
,
если эта функция определена в некоторой
окрестности точки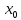 ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки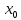 ,
и для каждого
,
и для каждого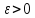 найдется
число
найдется
число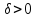 такое, что для всех
такое, что для всех ,
удовлетворяющих условию
,
удовлетворяющих условию ,
выполняется неравенство
,
выполняется неравенство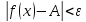 .
.
В этом случае пишут илипри.
б)
Определение предела по Гейне.
Число А называется пределом функции
f(x) в точке  ,
если эта функция определена в некоторой
проколотой окрестности точки
,
если эта функция определена в некоторой
проколотой окрестности точки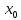 ,
т.е.
,
т.е.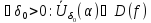 ,
и для любой последовательности {xn},
сходящейся к
,
и для любой последовательности {xn},
сходящейся к
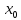 .
И такой, что
.
И такой, что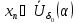 для всех
для всех
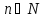 ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
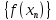 сходится к числу А.
сходится к числу А.
Теорема. Определения предела функции по Коши и по Гейне эквивалентны.
53. Непрерывные функции многих переменных.
Определение
1:
Функция
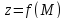 называется непрерывной в точке
называется непрерывной в точке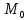 ,
если предел функции в этой точке
существует и равен значению функции в
этой точке, т.е.
,
если предел функции в этой точке
существует и равен значению функции в
этой точке, т.е.
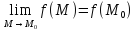 или
или
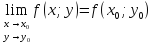
Определение
2:
Функция
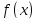 называется непрерывной в точке
называется непрерывной в точке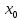 ,
если ее приращение в этой точке является
бесконечно малой функцией при
,
если ее приращение в этой точке является
бесконечно малой функцией при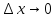
По аналогии с определением предела функции:
Определение
по Коши. Функция
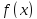 называется непрерывной в точке
называется непрерывной в точке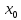 ,
если для любого
,
если для любого существует
существует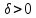 такое, что для всех
такое, что для всех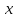 ,
удовлетворяющих условию
,
удовлетворяющих условию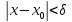 ,
выполняется неравенство
,
выполняется неравенство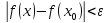 .
.
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.
Если
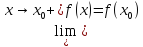 (
(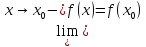 ),
то функцию
),
то функцию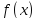 называют непрерывной в точке
называют непрерывной в точке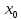 справа (слева). Если функция
справа (слева). Если функция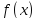 непрерывна в точке
непрерывна в точке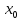 и слева, и справа, то она непрерывна в
этой точке. В данном случае, по теореме
связи между односторонними пределами
и пределом функции, предел функции в
точке
и слева, и справа, то она непрерывна в
этой точке. В данном случае, по теореме
связи между односторонними пределами
и пределом функции, предел функции в
точке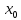 равен значению в этой точке
равен значению в этой точке
Теорема
об арифметических действиям над
непрерывными функциями:
Пусть
функции
 и
и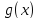 непрерывны в точке
непрерывны в точке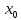 .
Тогда
.
Тогда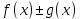 ,
,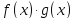 и
и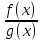 (при
(при
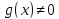 )
также
непрерывны в той точке.
)
также
непрерывны в той точке.
