
- •1. Натуральные числа.
- •1. Если функции иявляются бесконечно малыми, то функциятакже есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
- •2. Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая.
- •3. Произведение постоянной на бесконечно малую есть бесконечно малая.
- •4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
- •8. Первый замечательный предел. Второй замечательный предел
- •9. Критерий Коши сходимости последовательности
- •10. Предел функции, два определения.
- •12. Непрерывность функции. Разрывы первого и второго рода
- •13. Теоремы Вейерштрасса о функции непрерывной на отрезке.
- •14. Теорема о свойстве непрерывной на отрезке функции принимающей на концах отрезка значения разных знаков (Больцано-Коши).
- •15. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины.
- •16. Сравнение бесконечно больших величин. Эквивалентные бесконечно большие величины.
- •17.Применение эквивалентных бесконечно малых и бесконечно больших величин для вычисления пределов.
- •18 Производная функции. Механический и геометрический смысл производной.
- •Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •19 Свойства производных. Правила дифференцирования
- •20 Производные элементарных функций.
- •21 Производная сложной функции. Производная обратной функции
- •22 Дифференциал функции. Геометрический смысл
- •23 Приближенное выражение приращения функции через дифференциал.
- •24 Производная высшего порядка.
- •Формула Тейлора
- •34. Асимптоты
- •35. Выпуклость и вогнутость графика функции. Точки перегиба
- •43.Замена переменной и интегрирование по частям в определенном интеграле.
- •44.Приложение интегралов. Площадь плоской фигуры.
- •45.Несобственные интегралы 1-го и 2-го рода. Сходимость интегралов.
- •51.Предел последовательности n-мерных точек.
- •52. Предел функции многих переменных, два определения.
- •В этом случае пишут илипри.
- •53. Непрерывные функции многих переменных.
- •54. Частные производные первого порядка.
- •60. Градиент функции, свойства градиента
- •63. Необходимые условия локального экстремума дифференцируемой функции многих переменных. Стационарные точки.
- •64. Достаточное условие экстремума функции многих переменных.
- •65. Комплексные числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Эйлера. Вычисление корней многочленов.
- •66. Дифференциальные уравнения, основные понятия.
- •67. Дифференциальные уравнения с разделяющимися переменными.
- •68. Линейные уравнения первого порядка.
- •69. Линейные дифференциальные уравнения с постоянными коэффициентами второго порядка.
23 Приближенное выражение приращения функции через дифференциал.
Если
функция ![]() дифференцируема
в точке
дифференцируема
в точке ![]() ,
то на основании формулы (1) ее приращение,
соответствующее приращению
,
то на основании формулы (1) ее приращение,
соответствующее приращению ![]() ,
можно записать следующим образом:
,
можно записать следующим образом:
![]() .
.
Отсюда
следует, что дифференциал функции при
достаточно малых ![]() может
служить хорошим приближением приращения
функции. В этом смысле пишут приближенное
равенство
может
служить хорошим приближением приращения
функции. В этом смысле пишут приближенное
равенство
![]() ,
(7)
,
(7)
которым широко пользуются.
Пусть
надо вычислить значение функции ![]() в
точке
в
точке ![]() ,
т. е. число
,
т. е. число ![]() .
Однако появилась необходимость
заменить
.
Однако появилась необходимость
заменить ![]() его
приближенным значением
его
приближенным значением ![]() :
:
![]() .
.
Возникает приближенное равенство
![]() .
.
Его абсолютная погрешность равна
![]() .
.
Если
функция ![]() дифференцируема
в точке
дифференцируема
в точке ![]() ,
то из формулы (7) следует, что при
малых
,
то из формулы (7) следует, что при
малых ![]() можно
считать, что абсолютная погрешность
рассматриваемого приближения равна
приближению абсолютной величине
дифференциала функции:
можно
считать, что абсолютная погрешность
рассматриваемого приближения равна
приближению абсолютной величине
дифференциала функции:
![]() ,
,
вычисленного
для соответствующего приращения ![]() .
.
24 Производная высшего порядка.

25.Локальный экстремум. Теорема Ферма.
Точка ![]() называетсяточкой
локального максимума (или минимума)
функции
называетсяточкой
локального максимума (или минимума)
функции ![]() ,
сли существует такой окрестность
,
сли существует такой окрестность![]() этой
точки, принадлежащий области определения
функции, и для всех
этой
точки, принадлежащий области определения
функции, и для всех![]() из
этого окрестности выполняется
неравенство
из
этого окрестности выполняется
неравенство![]() (или
(или![]() ).
).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках - ее экстремальными значениями.
Теорема
Ферма. Пусть
функция
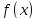 определена на интервале
определена на интервале
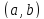 и в некоторой точке
и в некоторой точке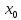 этого
интервала имеет наибольшее или наименьшее
значение. Тогда если в точке
этого
интервала имеет наибольшее или наименьшее
значение. Тогда если в точке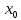 существует производная, то она равна
нулю, т.е.
существует производная, то она равна
нулю, т.е.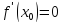
26.Теоремы Коши и Лагранжа о среднем.
Теорема
Коши. Пусть
функция
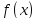 и
и
 непрерывны на
непрерывны на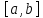 и дифференцируемы на
и дифференцируемы на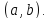 Пусть кроме того,
Пусть кроме того, .
.
Тогда
существует точка c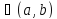 такая, что справедлива формула
такая, что справедлива формула
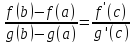 .
.
Теорема
Лагранжа. Пусть
на отрезке
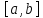 определена функция
определена функция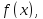 причём:
причём:
1.
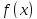 непрерывна на
непрерывна на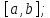
2.
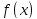 дифференцируема
на
дифференцируема
на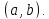
Тогда
существует точка c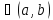 такая,
что справедлива формула
такая,
что справедлива формула
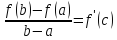
27.Раскрытие неопределенностей. Правило Лопиталя.
Раскрытие неопределённостей вида
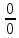 .
Первое правило Лопиталя.
.
Первое правило Лопиталя.
Если
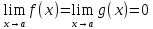 ,
то
,
то
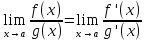 ,
когда последний предел существует
(конечный или бесконечный).
,
когда последний предел существует
(конечный или бесконечный).
Раскрытие неопределённости вида
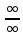 .
Второе правило Лопиталя.
.
Второе правило Лопиталя.
Если
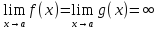 ,
то
,
то
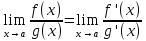 ,
когда последний предел существует
(конечный или бесконечный).
,
когда последний предел существует
(конечный или бесконечный).
Правила
верны и в том случае, когда
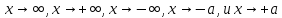 .
.
Неопределённости вида
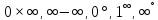 и
их раскрытие.
и
их раскрытие.
Неопределённости
вида
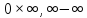 сводятся путём алгебраических образований
к неопределённостям вида
сводятся путём алгебраических образований
к неопределённостям вида
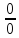 и
и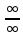 ,
а затем
раскрываются
с помощью правила Лопиталя.
,
а затем
раскрываются
с помощью правила Лопиталя.
Неопределённости
вида
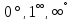 с помощью тождества
с помощью тождества
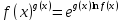
Сводятся
к неопределённости вида
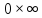 .
.
28.Формула Тейлора для функции.
Теорема
Тейлора. Пусть
функция f(x)
имеет в точке a
и некоторой её окрестности производные
порядка n+1.
Пусть x
– любое значение аргумента из
указанной окрестности,
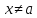 .
Тогда между точками а и х найдется точка
ξ такая,
что
справедлива
формула Тейлора.
.
Тогда между точками а и х найдется точка
ξ такая,
что
справедлива
формула Тейлора.
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Формула Тейлора
![]()
,
где Rn(x)(на
самом деле Rn+1(x))
-
называется
остаточные
членом в форме Лагранжа
и обозначается
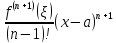 .
.
Так
как точка
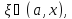 то найдется число
то найдется число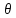 из интервале 0<
из интервале 0<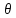 <
1 такое, что
<
1 такое, что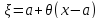 и остаточный член принимает вид
и остаточный член принимает вид
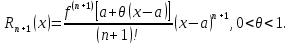
Если
функция
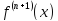 ограничена в окрестности точки
ограничена в окрестности точки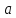 ,
то остаточный член
,
то остаточный член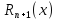 является
бесконечно малой более высокого
порядка, чем
является
бесконечно малой более высокого
порядка, чем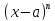 при
при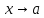 :
:
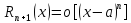 при
при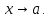
Последнее соотношение называется остаточным членом в форме Пеано.
Формулу Тейлора при а = 0 принято называть формулой Маклорена:
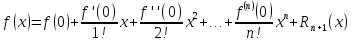 .
.
Остаточный член имеет вид:
1)
в
форме Лагранжа
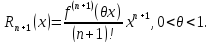
2)
в форме
Пеано
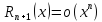 .
.
29.Формулы Тейлора элементарных функций.
Разложение элементарных функций по формуле Маклорена.
1)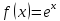 Так
как
Так
как
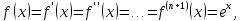
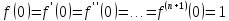 ,
,
то формула Маклорена имеет вид
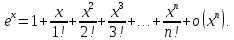
2)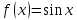 .
Так как
.
Так как
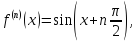
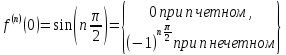 ,
,
то формула Маклорена имеет вид
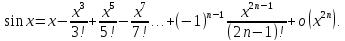
Остаточный
член записан в виде
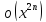 ,
а не в виде
,
а не в виде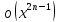 ,
так как следующий за последним член
равен нулю. Тоже самое относится и к
формуле сcos
x.
,
так как следующий за последним член
равен нулю. Тоже самое относится и к
формуле сcos
x.
3)
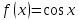 .
Тогда как
.
Тогда как
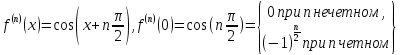 ,
,
то формула Маклорена имеет вид
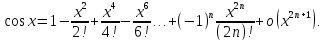
30.Приближенное вычисление функций по формуле Тейлора. Оценка погрешности.
Если
остаток в формуле Тейлора ![]() ,то формулу
Тейлора для многочлена можно записать
так: .
,то формулу
Тейлора для многочлена можно записать
так: .
В
свою очередь остаточный
член: ![]() — определяет
погрешность формулы.
— определяет
погрешность формулы.
31.Теорема о возрастании и убывании дифференцируемой функции.
Теорема 7.2. Пусть
функция ![]() дифференцируема
на интервале
дифференцируема
на интервале![]() и
и![]() при
всех
при
всех![]() .
Тогда
.
Тогда![]() возрастает
на
возрастает
на![]() .
Если же
.
Если же![]() при
всех
при
всех![]() ,
то
,
то![]() не
убывает на
не
убывает на![]() .
.
Аналогично,
если ![]() при
всех
при
всех![]() ,
то
,
то![]() убывает
на
убывает
на![]() ,
а если
,
а если![]() при
всех
при
всех![]() ,
то
,
то![]() не
возрастает на
не
возрастает на![]() .
.
Теорема 7.3 Если
дифференцируемая функция не убывает
на интервале ![]() ,
то
,
то ![]() при
всех
при
всех ![]() ;
если же функция не возрастает на
;
если же функция не возрастает на ![]() ,
то
,
то ![]() при
при ![]() .
.
32.Необходимые условия локального экстремума. Достаточные условия локального экстремума.
Теорема
1(необходимое условие локального
экстремума). Если
функция f(x)
имеет в точке x0
локальный
экстремум и дифференцируема в этой
точке, то
 .
.
Точки в которых производная функция равна 0, принято называть точками возможного экстремума.
Теорема
2(достаточное условие локального
экстремума). Пусть
функция f(x)
дифференцируема в некоторой δ-окрестности
точки x0.
Тогда если
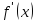 при переходе через точку x0
меняет знак с «+» на «-», то x0
- точка локального максимума, если f’(x)
в точке x0
меняет знак с «-» на «+», то x0
– точка локального минимума, если же
знак f’(x)
в точке x0
не изменился, то в точке x0
экстремума не существует.
при переходе через точку x0
меняет знак с «+» на «-», то x0
- точка локального максимума, если f’(x)
в точке x0
меняет знак с «-» на «+», то x0
– точка локального минимума, если же
знак f’(x)
в точке x0
не изменился, то в точке x0
экстремума не существует.
33.Наибольшее и наименьшее значения функции
Наибольшим
значением функции y=f(x) на
промежутке X называют
такое значение ![]() ,
что для любого
,
что для любого ![]() справедливо
неравенство
справедливо
неравенство ![]() .
.
Наименьшим
значением функции y=f(x) на
промежутке X называют
такое значение ![]() ,
что для любого
,
что для любого ![]() справедливо
неравенство
справедливо
неравенство ![]() .
.
Эти
определения интуитивно понятны:
наибольшее (наименьшее) значение функции
– это самое большое (маленькое) принимаемое
значение на рассматриваемом интервале
при абсциссе ![]() .
.
