, .

Нахождение точечных оценок математического ожидания и дисперсии по данным варианта осуществим с помощью расчетной таблицы.

i
1	9,2	5	46	5,1
2	9,4	8	75,2	5,25
3	9,6	15	144	5,58
4	9,8	22	215,6	3,7
5	10	25	250	1,1
6	10,2	30	306	0
7	10,4	23	239,2	0,83
8	10,6	20	212	3,04
9	10,8	18	194,4	6,27
10	11	8	88	4,99
11	11,2	6	67,2	5,88

180 1837,6 41,74

В статистических расчетах используют приближенные неравенства:

3. Выдвижение гипотезы о распределении случайной величины.

При выдвижении гипотезы (предположения) о законе распределения изучаемой случайной величины мы будем опираться лишь на внешний вид статистического распределения. А именно, будем руководствоваться тем, что профиль графика плотности теоретического распределения должен соответствовать профилю гистограммы: если середины верхних сторон прямоугольников, образующих гистограмму, соединить плавной кривой, то эта линия представляет в первом приближении график плотности распределения вероятностей.

Итак, Изобразим график и выпишем формулу плотности нормального (или гауссовского) распределения с параметрамии , где,:

f(x)

x

a

Сравнение построенной гистограммы и графика плотности распределения приводит к следующему заключению о предполагаемом (теоретическом) законе распределения в рассматриваемом варианте исходных данных:

Вариант 3 – нормальное (гауссовское) распределение.

4. Построение графика теоретической плотности распределения.

Чтобы выписать плотность теоретического (предполагаемого) распределения, определим значения параметров и для показательного распределения и подставим их в соответствующую формулу. Все параметры распределений тесно связаны с числовыми характеристиками случайной величины. Т.е.

Поскольку значения математического ожидания и дисперсии неизвестны, то их заменяют соответствующими точечными оценками, т.е используют (уже упомянутые ранее) приближенные равенство , ,что позволяет найти значения параметров распределения.

По исходным данным была выдвинута гипотеза о нормальном распределении изучаемой случайной величины. Найдем параметры этого распределения:

Следовательно, плотность предполагаемого распределения задается формулой

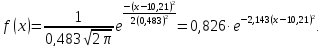
Теперь необходимо вычислить значения плотностипри (в серединах интервалов). Для этого воспользуемся следующей схемой:

значения функции

при находятся, например, с помощью таблицы, имеющейся в любом учебнике или задачнике по теории вероятностей и математической статистике.

9,2	-2,09	0,0449	0,093
9,4	-1,68	0,0973	0,207
9,6	-1,26	0,1804	0,373
9,8	-0,85	0,278	0,58
10	-0,43	0,3637	0,755
10,2	-0,02	0,3989	0,828
10,4	0,39	0,3697	0,766
10,6	0,81	0,2874	0,6
10,8	1,22	0,1895	0,393
11	1,63	0,1057	0,228
11,2	2,05	0,0488	0,103

Далее, на одном чертеже строим гистограмму и график теоретической плотности распределения: гистограмма была построена ранее, а для получения графика плотности наносим точки с координатами и соединяем их плавной кривой.