
- •«Статистические методы обработки экспериментальных данных»
- •Вариант № 3
- •Москва – 2012г Вариант №3
- •1. Построение интервального и точечного статистических распределений результатов наблюдений. Построение полигона и гистограммы относительных частот.
- •2. Нахождение точечных оценок математического ожидания и дисперсии.
- •, .
- •3. Выдвижение гипотезы о распределении случайной величины.
- •4. Построение графика теоретической плотности распределения.
- •5. Проверка гипотезы о распределении с помощью критерия согласия Пуассона.
- •5.1. Группировка исходных данных.
- •5.2. Вычисление теоретических частот.
- •5.3. Статистика и вычисление ее значения по опытным данным.
- •5.4. Распределение статистики .
- •5.5. Правило проверки гипотезы о законе распределения случайной величины.
- •5.6. Вывод о соответствии выдвинутой гипотезы и опытных данных в примерах.
5.4. Распределение статистики .
Случайная величина имеет
 -распределение с r
степенями свободы (r=1;2;3...),
если ее плотность имеет вид
-распределение с r
степенями свободы (r=1;2;3...),
если ее плотность имеет вид






x
r-2
0
где
 -
некоторая положительная постоянная
(
-
некоторая положительная постоянная
( -
определяется из равенства
-
определяется из равенства ).
Случайная величина, имеющая распределение
).
Случайная величина, имеющая распределение сrстепенями свободы,
будет обозначаться через
сrстепенями свободы,
будет обозначаться через .
.
Для дальнейшего изложения важно отметить,
что, во-первых, распределение
 определяется одним параметром – числомrстепеней свободы и,
во-вторых, существуют таблицы, позволяющие
приближенно найти вероятность попадания
значений случайной величины
определяется одним параметром – числомrстепеней свободы и,
во-вторых, существуют таблицы, позволяющие
приближенно найти вероятность попадания
значений случайной величины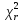 в любой промежуток.
в любой промежуток.
Вернемся теперь к статистике
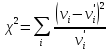 .Отметим, что она является случайной
величиной, поскольку зависит от
результатов наблюдений и, следовательно,
в различных сериях опытов принимает
различные значения, заранее не известные
значения. Понятно, кроме того, что закон
распределения статистики
.Отметим, что она является случайной
величиной, поскольку зависит от
результатов наблюдений и, следовательно,
в различных сериях опытов принимает
различные значения, заранее не известные
значения. Понятно, кроме того, что закон
распределения статистики
 зависит:
зависит:
1)от действительного (но неизвестного
нам) закона распределения случайной
величины, измерения которой осуществляются
(им определяются эмпирические частоты );
);
2)от количества произведенных наблюдений (от числаn) и от способа разбиения числовой оси на промежутки (в частности, от числа 1);
3)от теоретического (выдвинутого в
качестве гипотезы) закона распределения
изучаемой случайной величины (им
определяются теоретические вероятности
 и теоретические частоты
и теоретические частоты ).
).
Если выдвинутая гипотеза верна, то,
очевидно, закон распределения статистики
 зависит только от закона распределения
измеряемой случайной величины, от числаnи от выбора промежутков
разбиения. Но на самом же деле, в этом
случае (благодаря мастерски подобранному
Пирсоном выражения для
зависит только от закона распределения
измеряемой случайной величины, от числаnи от выбора промежутков
разбиения. Но на самом же деле, в этом
случае (благодаря мастерски подобранному
Пирсоном выражения для )
справедливо куда более сильное
утверждение. А именно, при достаточно
большихnзакон распределения
статистики
)
справедливо куда более сильное
утверждение. А именно, при достаточно
большихnзакон распределения
статистики
 практически не зависит ни от закона
распределения изучаемой случайной
величины и ни от количестваnпроизведенных опытов:при
практически не зависит ни от закона
распределения изучаемой случайной
величины и ни от количестваnпроизведенных опытов:при
 распределение статистики
распределение статистики
 стремится к
стремится к
 -
распределению с r
степенями свободы. Эта теорема
объясняет, почему статистика Пирсона
обозначается через
-
распределению с r
степенями свободы. Эта теорема
объясняет, почему статистика Пирсона
обозначается через .
.
Если в качестве предполагаемого выбрано одно из трех основных непрерывных распределений (нормальное, показательное или равномерное), то
 ,
,
где
 - количество промежутков, на которое
разбита числовая ось (количество групп
опытных данных). В общем случае
- количество промежутков, на которое
разбита числовая ось (количество групп
опытных данных). В общем случае
 ,
,
Nпар –
количество параметров предполагаемого
распределения, которые заменены
вычисленными по опытным данным оценками.
Т.е. в данном варианте после группировки
исходных данных получаем количество
промежутков разбиения
 ,
, ,
т.к. количество параметров предполагаемого
распределения, которые заменены
вычисленными по опытным данным оценкам,
равно 2 – это
,
т.к. количество параметров предполагаемого
распределения, которые заменены
вычисленными по опытным данным оценкам,
равно 2 – это для нормального распределения.
Следовательно,
для нормального распределения.
Следовательно,

5.5. Правило проверки гипотезы о законе распределения случайной величины.
Статистика
 принимает только неотрицательные
значения (всегда
принимает только неотрицательные
значения (всегда ),
причем в нуль она обращается в
одном-единственном случае – при
совпадении всех соответствующих
эмпирических и теоретических частот
(то есть при
),
причем в нуль она обращается в
одном-единственном случае – при
совпадении всех соответствующих
эмпирических и теоретических частот
(то есть при для каждого
для каждого ).
).
Если выдвинутая гипотеза о законе
распределения изучаемой случайной
величины соответствует действительности,
то эмпирические и теоретические частоты
должны быть примерно одинаковы, а
значит, значения статистики
 будут сгруппированы около нуля. Если
же выдвинутая гипотеза ложна, то
эмпирические и соответствующие
теоретические частоты будут существенно
разниться, что приведет к достаточно
большим отклонениям от нуля значений
будут сгруппированы около нуля. Если
же выдвинутая гипотеза ложна, то
эмпирические и соответствующие
теоретические частоты будут существенно
разниться, что приведет к достаточно
большим отклонениям от нуля значений
 .
.
Поэтому хотелось бы найти тот рубеж –
называемый критическим значением(или критической точкой) и обозначаемый
через ,
который разбил бы всю область возможных
значений статистики
,
который разбил бы всю область возможных
значений статистики
 на два непересекающиеся подмножества:область принятия гипотезы,
характеризующаяся неравенством
на два непересекающиеся подмножества:область принятия гипотезы,
характеризующаяся неравенством ,
икритическую область (или область
отвержения гипотезы), определяемую
неравенством
,
икритическую область (или область
отвержения гипотезы), определяемую
неравенством .
.
Область принятия Критическая
гипотезы область



0


Если выдвинутая гипотеза о законе
распределения изучаемой случайной
величины верна, то вероятность попадания
значений статистики
 в критическую область должна быть мала,
так что событие (
в критическую область должна быть мала,
так что событие ( )
должно быть практически неосуществимым
в единичном испытании. Эта вероятность,
обозначим ее через α :
)
должно быть практически неосуществимым
в единичном испытании. Эта вероятность,
обозначим ее через α :
 ,
,
называется уровнем значимости.
Чтобы
определить критическое значение
 ,
поступим следующим образом. Зададим
какое-либо малое значение уровня
значимости и найдем
,
поступим следующим образом. Зададим
какое-либо малое значение уровня
значимости и найдем как корень уравнения
как корень уравнения

и приближенное значение
 можно найти из уравнения
можно найти из уравнения
 .
.
Геометрические соображения показывают,
что после уравнение имеет единственное
решение: его корень – это такое число
 ,
при котором площадь под графиком функции
,
при котором площадь под графиком функции (плотности
(плотности -
распределения) над участком
-
распределения) над участком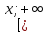 равнаα. На практике решение
последнего уравнения находят с помощью
специальных таблиц. Эти таблицы позволяют
по двум входным параметрам – уровню
значимостиαи числу степеней
свободы определить критическое значение
равнаα. На практике решение
последнего уравнения находят с помощью
специальных таблиц. Эти таблицы позволяют
по двум входным параметрам – уровню
значимостиαи числу степеней
свободы определить критическое значение .
.
Зададим уровень значимости как
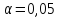 (условие курсовой работы).
(условие курсовой работы).
Подводя итоги, сформулируем правило
проверки гипотезы о законе распределения
случайной величины с помощью
 - критерия Пирсона:
- критерия Пирсона:
1.Проводят независимых наблюдений случайной
величины (принято считать, что должно
быть
независимых наблюдений случайной
величины (принято считать, что должно
быть )
)
2.Разбивают всю числовую ось на несколько (как правило, на 8…12) промежутков

так, чтобы количество результатов
измерений в каждом из них (называемое
эмпирической частотой
 )
оказалось не менее пяти.
)
оказалось не менее пяти.
3. Выдвигают (например, судя по профилю гистограммы) гипотезу о законе распределения изучаемой случайной величины и находят параметры этого закона (чаще всего, заменяя математическое ожидание и дисперсию их оценками).
4.С помощью предполагаемого
(теоретического) распределения находят
теоретические вероятности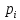 и теоретические частоты
и теоретические частоты
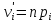 попадания значений случайной величины
в
попадания значений случайной величины
в
 -йпромежуток.
-йпромежуток.
5.По эмпирическим и теоретическим
частотам вычисляют значение статистики ,
обозначаемое через
,
обозначаемое через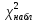 .
.
6.Определяют число степеней свободы.
степеней свободы.
7.Используя заданное значение
уровня значимостиαи найденное
число степеней свободы ,
по таблице находят критическое значение
,
по таблице находят критическое значение
 .
.
8. Формулируют вывод, опираясь наосновной принцип проверки статистических гипотез:
если наблюдаемое значение принадлежит
критической области, то есть если
 ,
то гипотезу отвергают как плохо
согласующуюся с результатами эксперимента
;
,
то гипотезу отвергают как плохо
согласующуюся с результатами эксперимента
;
если наблюдаемое значение критерия
принадлежит области принятия гипотезы,
то есть если
 ,
то гипотезу принимают как не противоречащую
результатам эксперимента.
,
то гипотезу принимают как не противоречащую
результатам эксперимента.
