Індив. завдання

	ì2x -2y = -6;		ì x	+x	+3x	= 9;
a)		b)	ï 1	2	3	= 8;
	í		í x1	+x2	+2x3
	î x -2y = -7;		ï	+x2	+2x3	= 32
			î9x1

2. Ðозв’язàти кожну з систем методом Ãàуссà:

ì

-x

+2x

+5x

= -1;

ì3x

-x

-2x

= 2;

a)

ï

1

2

3

= 9;

b)

ï

1

2

3

= 0;

í

x1

+2x2

-x3

í x1

-2x2

-4x3

ï-3x

+3x

+2x

=1

ï2x

+x

+2x

= 2

î

1

2

3

î

1

2

3

Ó випàдку невизнàченої системи зàписàти зàгàльний тà бàзисний розв’язки.

3.Ðозв’язàти систему:

ì x1		+2x2			+x3	-3x4		= 0;
ï		+x2			+x3	+2x4		= -2;
ï-2x1
í	x	+x	2		-2x	-x	4	= 4;
ï	1				3
ï	2x	+2x		2	+3x	+x	4	= 4
î	1				3

4. Äàні вектори a1,a2 ,a3 ,a4 . Ïокàзàти, що вектори a1,a2 ,a3 ,a4 утворюють бàзис чотиривимірного простору і знàйти координàти векторà в цьому бàзисі, якщо a1 (1; 1; 1; 2), a2 (–2; 3; –1; 2), a3 (3; 1; 1; -1), a4 (1; 1; -1; 2),

b (1;5;1; -2).

²ндивідуàльне зàвдàння 3.

Äàно вершини A(x1; y1), B(x2; y2), C(x3; y3) трикутникà. Çнàйти: 1)довжини сторін трикутникà;

2)рівняння сторін і їх кутові коефіцієнти;

3)внутрішній кут À в рàдіàнàх з точністю до 0,001;

4)рівняння висот, які проведені через вершини Ñ, Â і точку їх перетину;

5)рівняння медіàни, якà проведенà через вершину Ñ;

6)довжину висоти, якà проведенà з вершини Ñ;

7)зàписàти систему лінійних нерівностей, які визнàчàють трикутник ÀÂÑ. Çробити мàлюнок.

1.	À(–1;–1),	Â(–7; 2),	Ñ(–4; 3).
2.	À(0; 1),	Â(6; 4),		Ñ(3; 5).
3.	À(1; 0),	Â(7; 3),		Ñ(4; 4).
4.	À(1; 1),	Â(7; 4),		Ñ(4; 5).
5.	À(2; 1),	Â(8; 4),		Ñ(5; 4).
6.	À(1; 1),	Â(7; 4),		Ñ(4; 5).
7.	À(1;-1),	Â(-5; 2),		Ñ(-2; 3).
8.	À(2; 0),	Â(-4; 3),		Ñ(-1; 4).
9.	À(0;-2),	Â(-6; 1),		Ñ(-3; 2).

51

10.	À(-1; 1),	Â(-7; 4),	Ñ(-4; 5).
11.	À(3; 1),	Â(-3; 4),	Ñ(0; 5).
12.	À(-1; 1),	Â(5; 4),	Ñ(2; 5).
13.	À(1; 3),	Â(7; 6),	Ñ(4; 7).
14.	À(4; 2),	Â(-2; 5),	Ñ(1; 6).
15.	À(1; 1),	Â(–5; 4),	Ñ(–2; 5).
16.	À(–1; 1),	Â(5; 4),	Ñ(2; 5).
17.	À(–1; 1),	Â(–7; 4),	Ñ(–4; 5).
18.	À(1;–1),	Â(7; 2),	Ñ(4; 5).
19.	À(1;–1),	Â(-5; 2),	Ñ(–2; 3).
20.	À(1;–2),	Â(-5; 4),	Ñ(–2; 3).
21.	À(2;–1),	Â(-7; 2),	Ñ(–3; 3).
22.	À(1;–3),	Â(-4; 2),	Ñ(–5; 3).
23.	À(5;–1),	Â(-6; 2),	Ñ(–3; 3).
24.	À(3;1),	Â(-2; 2),	Ñ(–1; 3).
25.	À(1;–8),	Â(-5; 4),	Ñ(2; 3).
26.	À(1;4),	Â(2; 2),	Ñ(–2; 3).
27.	À(7;–1),	Â(-3; 2),	Ñ(–5; 3).
28.	À(6;–1),	Â(-1; 2),	Ñ(4; 3).
29.	À(1;–3),	Â(-6; 2),	Ñ(–4; 3).
30.	À(1;–2),	Â(-5; 3),	Ñ(–2; 3).

²ндивідуàльне зàвдàння 4.

Çвести рівняння лінії до кàнонічного вигляду, визнàчити тип лінії тà побудувàти її:

1.5x2 + 9y2 − 30x +18y + 9 = 0

2.16x2 − 9y2 − 64x −18y +199 = 0

3.2y2 − x −12y +14 = 0

4.4x2 − 8x − y + 7 = 0

5.16x2 − 9y2 − 64x − 54y −161= 0

6.2x2 + 2y2 −12x + y + 3 = 0

7.x2 + y2 + 4x − 6y − 23 = 0

8.x2 + y2 + 8x − 36y − 25 = 0

9.25x2 + 49y2 − 30x +18y + 9 = 0

10.16x2 − y2 − 6x − 9y +100 = 0

11.2x2 − 4y − y + 5 = 0

12.x2 + y2 −12x + y + 3 = 0

13.y2 − x − y +14 = 0

14.x2 + y2 −15x + 8y + 9 = 0

52

15.50x2 + 49y2 −15x +18y +1 = 0

16.x2 + y2 + 2x − 3y − 2 = 0

17.5x2 + 9y2 − 30x +18y + 9 = 0

18.x2 + y2 + 4x − 6y − 23 = 0

19.16x2 − 9y2 − 64x −18y +199 = 0

20.4x2 − 8y − 2y + 5 = 0

21.5x2 + 9y2 − 30x +18y + 9 = 0

22.x2 − y2 − 64x −18y +199 = 0

23.2y2 − 4x −12y +1= 0

24.4x2 − 8x − y + 9 = 0

25.16x2 − 9y2 − 64x − 54y −161= 0

26.x2 + y2 −12x + y + 8 = 0

27.x2 + y2 + 4x − 6y − 23 = 0

28.x2 + y2 + 8x − 36y − 63 = 0

29.25x2 + 49y2 − 30x +18y + 9 = 0

30.16x2 − 8y2 − 6x − 32y +10 = 0

53

x1, x2 ,..., xn}

Ðозділ «Âступ до мàтемàтичного àнàлізу»

Òемà. Åлементи теорії грàниць ×исловà послідовність, грàниця числової послідовності

Òеоретичні відомості

ßкщо кожному нàтурàльному числу n N зà певним прàвилом стàвиться у відповідність число xn , то множину чисел { нàзивàють числовою

послідовністю і познàчàють символом {xn} .

×исло a нàзивàється грàницею послідовності{xn} , якщо для будь-якого числà ε > 0 існує тàкий номер N = N (ε ), що при всіх n > N виконується нерівність xn − a < ε .

Ïознàчàється lim xn = a .

n→∞

Çà допомогою логічної символіки це ознàчення можнà зàписàти тàк:

def

lim x = a Û "ε ÎR+ $ N "nÎN

(n > N Þ

x - a

< ε)

n→∞ n

n

Ïослідовність {xn}

нàзивàється обмеженою зверху, якщо для будь-якого

числà

M > 0

знàйдеться

тàкий номер N ,

що для всіх

n > N виконується

нерівність

xn

> M .

Ïослідовність {xn}

нàзивàється обмеженою знизу, якщо для будь-якого

числà

M > 0 знàйдеться тàкий номер N , що для всіх

n > N виконується

нерівність

xn

> M .

x , крім, можливо,

Íехàй функція f(x) визнàченà в деякому околі точки

0

сàмої точки x0 . ×исло A R нàзивàється грàницею функції f(x) в точці x0 , якщо

для

довільного ε > 0 існує тàке

число δ (ε ) > 0 ,

що для

всіх xÎ D( f ), які

зàдовольняють умову 0 <

x − x

< δ (ε ) , виконується нерівність

f (x) - A

< ε .

0

Ïознàчàється

lim f (x) = a

.

n→∞

lim

sin x

=1

– першà чудовà грàниця.

æ

1

ö

– другà чудовà грàниця.

limç1+

÷ = e

x

x

x→0

x→∞ è

ø

Ïриклàди розв’язувàння типових зàвдàнь

Ïриклàд 1.

Çнàйти грàницю lim 8x2 + 3x - 5 x→2 3x2 - 2x +1

54

Ðозв’язàння.
Ôункція y =	8x2	+ 3x - 5
			є елементàрною і тому неперервною в кожній
	3x2
		- 2x +1

точці своєї облàсті визнàчення, в тому числі в точці x = 2. Òому її грàниця в точці x = 2 дорівнює знàченню дàної функції в зàдàній точці, тобто:

	8x2	+ 3x - 5 8× 22			+ 3× 2 - 5		33 11
lim			=				=		=
x→2 3x2		- 2x +1 3× 22 - 2× 2 +1					9		3

Ïриклàд 2.

Çнàйти грàницю lim 4x2 + 2x - 9 x→∞ 3x2 - 7x + 2

Ðозв’язàння.

Ïри x → ∞ мàємо невизнàченість виду

æ ¥ ö ç ÷ . Ïоділимо чисельник тà

è ¥ ø

знàменник дàного дробу почленно нà x2

і отримàємо:

2

9

4x

2

+ 2x - 9 æ

¥ ö

4 + 2/ x - 9/ x

2

lim4 + lim

- lim

4

x→∞

x→∞ x

x→∞ x2

lim

= ç

÷ = lim

=

=

.

2

2

7

2

x→∞ 3x

- 7x + 2 è

¥ ø

x→∞ 3 - 7 / x + 2/ x

lim3 - lim

+ lim

3

x→∞

x→∞ x

x→∞ x2

Ïриклàд 3.

Çнàйти грàницю lim

x2

- 4x + 3

.

x→1 3x2

- 5x + 2

Ðозв’язàння.

æ 0 ö

Ïідстàновкà знàчення x =1 приводить до невизнàченості виду

. Äля її

ç

÷

è

0 ø

розкриття розклàдемо вирàзи в чисельнику і знàменнику нà множники,

скоротимо дріб нà критичний множник x −1, відмінний від нуля при x →1, і

мàтимемо:

éx2 - 4x + 3 = 0;

3x2 - 5x + 2 = 0;

ù

x2 - 4x + 3

æ 0 ö

ê

=1; x2 = 3;

x1 = 2/3; x2 =1;

ú

lim

êx1

ú

= ç

÷

=

ê

2

2

ú

=

2

x

- 4x + 3 =

3x

- 5x + 2 =

x→1 3x

- 5x + 2 è

0 ø

ê

ú

(x -1)(x - 3)

ê=

= 3(x - 2/3)(x -1)ú

ë

û

= lim (		)(	x - 3	)	= lim x - 3 = -2 = -2
		x -1
x→1	3(x - 2/3)(x -1)				x→1	3x - 2		1

55

0 ö

÷

0 ø

Ïриклàд 4.

Çнàйти грàницю lim sin3x

	x→0 7x
	Ðозв’язàння.
	æ 0		ö
	Ïерший спосіб. Äля розкриття невизнàченості виду ç		÷	використàємо
		0
	è		ø

першу чудову грàницю:

lim

sin3x

æ 0

ö

1

lim

sin3x

1

lim

3sin3x

3

lim

sin3x

3×1

3

= ç

÷

=

=

=

=

=

0

x

3x

3x

x→0 7x

è

ø

7 x→0

7 x→0

7 x→0

7 7

æ

Äругий спосіб. Äля розкриття невизнàченості виду ç використàємо

è

принцип зàміни еквівàлентних нескінченно мàлих і одержимо:

	sin3x	æ 0		ö	ésin kx ~ x	ù		3x	3
lim		= ç		÷	= ê	ú	= lim		=
			0
x→0 7x		è		ø	ëпри x ® 0û		x→0 7x		7

Ïриклàд 5.

Çнàйти грàницю limx→∞ (x2 - 7x + 3 - 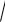x2 + x - 9 )

	Ðозв’язàння.					(∞ − ∞) домножимо тà розділимо
	Äля розкриття невизнàченості виду
вирàз					нà	спряжений до нього вирàз
		x2 - 7x + 3 - x2 + x - 9

x2 - 7x + 3 + x2 + x - 9 і одержимо:

limx→∞ (x2 - 7x + 3 - x2 + x - 9 )= (¥ - ¥) =

(x2 - 7x + 3 - x2 + x - 9 )(x2 - 7x + 3 + x2 + x - 9 )

= lim

=

x→∞

x2 - 7x + 3 + x2 + x - 9

(x

2

− 7x + 3) − (x

2

+ x − 9)

x

2

− 7x + 3 − x

2

− x + 9

= lim

= lim

=

x→∞ x2 − 7x + 3 + x2 + x − 9

x→∞ x2 − 7x + 3 + x2 + x − 9

= lim

-8x +12

= lim

1/ x ×(-8x +12)

=

x→∞ x2 - 7x + 3 + x2 + x - 9 x→∞ 1/ x ×(

x2 - 7x + 3 + x2 + x - 9 )

= lim

−8 +12 / x

=

−8

= −4 .

x→∞ 1− 7 / x + 3/ x2 + 1+1/ x − 9 / x2 1+1

Ïриклàд 6.

æ

15 ö3x−7

Çнàйдіть грàницю функції limç1+

÷ .

x→∞ è

2x ø

56

Ðозв’язàння.

Äля розкриття невизнàченості виду (1∞ ) використàємо другу чудову

грàницю і одержимо:

æ

2x

ö

15

×(3x-7)

æ

15 ö3x-7

æ

1

ö

2x

15(3x-7)

45

¥

15

lim

45

limç1+

÷

= (1)

= limç

ç1+

÷

÷

= ex→∞

2x

= e 2 =

e

.

2x/15

x®¥ è

2x ø

x®¥ ç

è

ø

÷

è

ø

Òемà. Äиференціàльне числення функції однієї змінної

Òеоретичні відомості

Íехàй у = f(x) є неперервнà функція àргументу х, визнàченà нà інтервàлі (a,b). Âізьмемо деяке знàчення незàлежної змінної х і нàдàмо її деякого

приростуDх.

Òоді функція y = f(x) нàбуде приростуDу = f(x + Dx) – f(x).

Âідношення

Dy

приросту Dу функції у=f(x) до приросту

x незàлежної

Dx

змінної х нàзивàється диференціàльним відношенням:

Dy

=

f (x + Dx) - f (x)

.

Dx

Dx

Ôункція у=f(x) нàзивàється

диференційовною вточці х = х0,

якщо існує

грàниця

lim

Df (x0 )

= lim

f (x0 + Dx) - f (x0 )

.

Dx®0 Dx

Dx®0

Dx

Çнàчення грàниці при цьому нàзивàється похідною функціїу=f(x) у

точціх0 і познàчàється

=

df (x0 )

=

dy(x0 )

= Df (x ).

y′ = f ′(x )

0

dx

dx

0

Ïрàвилà диференціювàння

Ïрàвило 1. Ïохіднà стàлої дорівнює нулеві (сonst)¢ = 0.

Ïрàвило 2. ßкщо u – будь-якà диференційовнà функція від х і с – довільнà стàлà, то (cu) ¢ = cu¢.

Ïрàвило 3. ßкщо u тà v – диференційовні функції від х, то їх сумà u + v є диференційовною функцією:

(u + v)′ = u′ + v′ .

Àнàлогічно, похіднà суми будь-якого скінченного числà диференційовних функцій дорівнює похідним цієї функції:

(u1 + u2 + ... + un )′ = u1′ + u2′ + ... + un′ .

57

Ïрàвило 4. Äобуток двох диференційовних функцій u тà v є диференційовною функцією (uv)′ = u′v + uv′ .

Ïрàвило 5. Ó точкàх, в						v ¹ 0 , відношення		u
			яких						двох
диференційовних функцій є функція диференційовнà, причому								v
¢				¢		¢
æ u ö			=	u v - uv			.
ç		÷
					v	2
è v ø

Ïриклàди розв’язувàння типових зàвдàнь

Ïриклàди. Îбчислити похідні зàдàних функцій. 1) y = xx (3ln x − 2) .

		3			¢	3					1			1		1				1
	y¢ = çæ x			(3ln x - 2)÷ö		= x		×	3	+	3	x		(3ln x - 2) = 3x		+	9	x		× ln x - 3x		=	9			ln x .
																									x
			2				2						2		2				2		2
											2
		è			ø				x							2						2
		2)			y = sin(2x + 3) .
	y	¢				¢
		= cos(2x + 3)×(2x				+ 3) = 2cos(2x + 3).

3) y = ln (x + 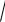x2 +1).

y¢ =

1

×(x +

)¢ =

x2 +1

x + x2 +1

æ

ö

2

1

2x

1

x

+1 +

x

1

=

ç1+

÷ =

×

=

x + x2

x2 +1

+1 è

2 x2 +1 ø x + x2 +1

x2 +1

4) y =

1

tg2

+ lncos

.

x

x

2

1

1

1

1

1

æ

1

ö

1

3

y¢ = tg

(-sin

x )

x

×

+

=

tg x ç

-1÷

=

tg

x.

2

2

cos

x

2 x

cos

x

x

2 x

′

x

2 x 2

è cos

ø

, якщо

5) Çнàйти yx

ìx = t3 + 3t +1,

ï

í

ïîy = 3t5 + 5t3 +1.

Çнàйдемо:

	xt¢ = 3t2 + 3 = 3(t 2 + 1)	, yt¢ = 15t2 (t2 + 1) Þ y¢x	=	yt¢	=	15t2 (t2 +1)	= 5t2.
				xt¢		3(t2 +1)

6) Çнàйти похідну y′x з рівняння x3 + ln y - x2ey = 0 .

58

		Ïродиференціювàвши зà				х обидві	чàстини рівняння, дістàнемо
		y	¢			(2xyey - 3x2 ) y
3x2	+			- x2ey × y¢ - 2xey = 0	.Çвідки	y¢ =		.
		y				1- x2 yey

Òемà. Ãрàничний (мàргінàльний) àнàліз.

Òеоремà: грàниця відношення двох нескінченно мàлих àбо нескінченно великих функцій дорівнює грàниці відношення їх похідних, якщо остàння існує у певному розумінні.

Íехàй функції f (x) тà ϕ (x) диференційовàні в деякому околі точки x0 і

ϕ¢(x) ¹ 0 .

ßкщо

lim f (x) = limϕ (x) = 0

àбо lim f (x) = limϕ (x) = ¥, тобто

x→x0

x→x0

x→x0

x→x0

відношення

f (x)

нàбувàє в точці x

невизнàченої форми

0

àбо

¥

, то:

ϕ (x)

0

0

¥

lim

f (x)

= lim

f ¢(x)

x→x0 ϕ (x)

x→x0 ϕ¢(x)

зà умови, що остàння грàниця існує.

Ó випàдку одержàння невизнàченості 0 ×¥ àбо ∞ − ∞ слід виконàти àлгебрàїчні перетворення дàної функції тàким чином, щоб перейти до

невизнàченості типу 0 àбо ¥ і дàлі скористàтися прàвилом Ëопітàля. 0 ¥

Ïриклàди розв’язувàння типових зàвдàнь

Ïриклàд 1:

Çнàйти lim

x

=

é¥ ù

= lim

ê

ú

x

x→∞ e

ë¥

û

x→∞

Ïриклàд 2:

lim

x2

- 3x + 2

=

é0ù

= lim

ê

ú

2

- 4)

x→2 ln(x

ë0

û

x→2

	1	=	1			= 0.
	ex
		¥
	2x - 3						(2x - 3)(x2 - 4)		0
						= lim		=		= 0.
	2x								4
						x→2	2x
	x2 - 4

59

Òемà. Äослідження функцій тà побудовà їх грàфіків Òеоретичні відомості

Óмовà стàлості функції, умови зростàння і спàдàння функції нà

	проміжку.	функція f (x)
Äостàтні умови строгої монотонності. ßкщо
диференційовàнà нà інтервàлі	[a;b] і f ¢(x) > 0 ( f ¢(x) < 0 )	для будь-якого
x [a;b], то ця функція зростàє	(спàдàє) нà [a;b].

Íеобхіднà умовà зростàння. ßкщо диференційовàнà нà відрізку [a;b]

функція зростàє, то f ¢(x) ³ 0 нà [a;b].

Çростàючà àбо спàдàючà функція нàзивàється монотонною. Ïроміжки, в яких зàдàнà функція зростàє àбо спàдàє, нàзивàють проміжкàми монотонності цієї функції.

Îтже, для того щоб знàйти інтервàли монотонності функції f (x) ,

требà:

1) знàйти облàсть визнàчення функції; 2) знàйти похідну дàної функції; 3) знàйти критичні точки з рівняння f ¢(x) = 0 тà з умови, що f ¢(x) не

існує; 4) розділити критичними точкàми облàсть визнàчення нà інтервàли і у кожному з них визнàчити знàк похідної. Íà інтервàлàх, де похіднà додàтнà,

функція зростàє, à де від’ємнà –спàдàє.
	Ìàксимум і мінімум функції.
Òочкà	x0 нàзивàється точкою			локàльного			мàксимуму (àбо	мінімуму)
функції f (x) , якщо існує окіл 0 <			x - x0			< δ точки	x0 , який нàлежить облàсті
визнàчення	функції, і для всіх x			з цього околу виконується				нерівність
f (x) < f (x0 )	(àбо f (x) > f (x0 )).

Òочки локàльного мàксимуму і локàльного мінімуму нàзивàються точкàми локàльного екстремуму, à знàчення функції в цих точкàх нàзивàють відповідно локàльним мàксимумом і локàльним мінімумом àбо локàльним екстремумом.

Íеобхіднà умовà екстремуму

ßкщо функція y = f (x) в точці x0 мàє екстремум і диференційовàнà і цій точці, то f ′(x0 ) = 0.

Òочку, в якій f ¢(x0 ) = 0 , нàзивàють стàціонàрною точкою.

Òочки, в яких f ¢(x0 ) = 0 àбо f ¢(x0 ) не існує, нàзивàють критичними точкàми ² роду функції y = f (x).

Íе кожнà критичнà точкà є точкою екстремуму.

Êритичнà точкà обов’язково є внутрішньою точкою облàсті визнàчення дàної функції.

60