Розв’язок:

Нехай і позначають потенціали електричного поля зовні і всередині сфери. Вважаємо, що заряд знаходиться на полярній осі. В цьому випадку потенціали поля повинні бути аксиально симетричними. Інакше кажучи, робимо висновок, що вони не повинні залежати від азимутального кута : і .

Потенціал задовольняє рівнянню Лапласа

(6.1)

у всіх точках , крім точки . Потенціал задовольняє рівнянню Лапласа

(6.2)

у всіх точках без виключення.

На поверхні сфери потенціали і повинні задовольняти граничним умовам: а) неперервності потенціала і б) розривності його радіальних похідних:

, (6.3)

. (6.4)

Згідно (), розв’язок рівняння (6.2) в області має структуру:

. (6.5)

Для побудови розв’язку рівняння (6.1) виділимо в потенціалі сингулярний внесок точкового заряду:

.

Тоді, складова потенціалу буде задовольняти рівнянню Лапласа:

у всіх точках . Його розв’язок буде подібним до (6.5):

. (6.6)

При потенціал повинен залишатись обмеженим, оскільки на початку координат, тобто в центрі сфери, точкові заряди є відсутніми. Тому (6.5) переходить у

. (6.7)

При потенціал і його складова повинні прямувати до нуля, оскільки всі заряди розташовані в обмеженій області простору. Тому

. (6.8)

Для знаходження коефіцієнтів розкладу і скористаємось граничною умовою (6.3) неперервності потенціала:

. (6.9)

Розкладемо в ряд за полінома Лежандра (див.()):

.

Враховуючи незалежність поліномів Лежандра, отримуємо наступне рівняння для коефіцієнтів:

. (6.10)

Його треба доповнити умовою постійності потенціалу на поверхні сфери, тобто умовою незалежності потенціалу сфери від кута . З цього випливає, що

. (6.11)

Комбінуючи (6.10) і (6.11), знаходимо:

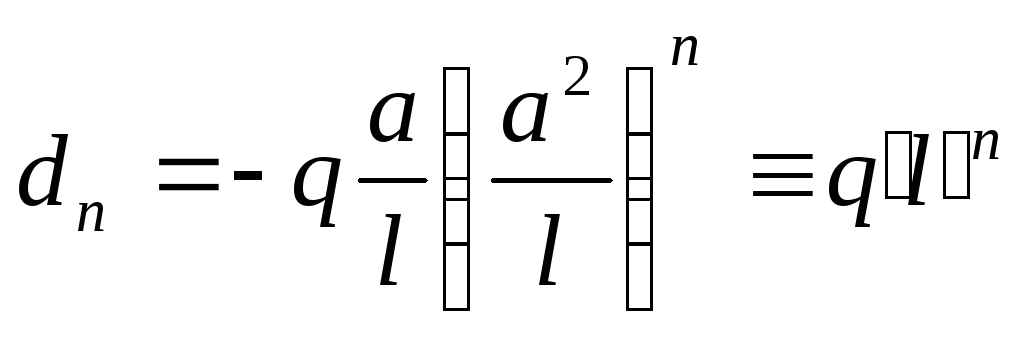, , (6.12)

. (6.13)

Для знаходження і скористаємось другою граничною умовою (6.4), надавши їй дещо іншого вигляду. Оскільки, індукований заряд сфери дорівнює нулю, так само як і напруженість поля всередині сфери, то (6.4) можна переписати у вигляді:

, (6.14)

де - елемент тілесного кута. Формула (6.14) припускає подальше спрощення:

.

З (6.13), таким чином, випливає, що .

Ряд (6.8) з коефіцієнтами (6.12) легко підсумовується:

. (6.15)

Це дозволяє шуканий потенціал електричного поля представити у вигляді:

, (6.16)

де

, і . (6.17)

Бачимо, що електричне поле зовні сфери утворюється заданим зарядом , а також двома зарядами зображеннями протилежних знаків: і , які розташовані в точках і відповідно.