Практикум по математическому анализу

2)L – параболас осью симметрии Оу и проходящая через точки О и А;

3)L – парабола, проходящаячерез О и А с осью симметрии Ох;

4)L –ломанная ОВА;

5)L – ломанная ОСА;

4. Вычислить:
Где	линия	L	–	задана	уравнениями
5. Даны функции					и точки

А(3,6), В(3,0), С(0,6). Вычислить криволинейный интеграл

Где:

1)L – отрезок ОА;

2)L – ломанная ОВА;

3)L – ломанная ОСА;

4)L – парабола, симметрическая относительно оси Оу и проходящая через точки О и А;

5)Проверить выполнение условия Грина.

Отреок ОА может быть записан в виде и

1)Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:

А)ОВ: здесь

откуда:

b) BA:

и

Таким образом:

2) Этот интеграл вычислим аналогично предыдущемую

А) ОС: т.е. dx=0), откуда

Б) СА:

Окончательно

3)Подставив координаты точки А(3;6) в равенство найдем уравнение данной параболы . При этом

Имеем:

Т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1)-4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.

Задания для самосоятельного решения:

1.Вычислить:

2.Вычислить:

Криволинейные интегралы первого рода. Связь между различными интегралами

x

1.Криволинейный интеграл первого рода.

2.Формула Грина.

3.Интегрирование полного дифференциала.

Теоретическая часть:

Криволинейный интеграл первого рода.

Пусть К – некоторая кусочно-гладкая плоская кривая:

x t , y y t t , , dS						dx	2	dy	2	- дифференциал дуги;
dt 0 dS			y
	x	2		2	.

Если f(x,y) – непрерывна на К, то под её криволинейным интегралом

первого рода понимается интеграл вида:			f
		K
Если кривая К задана y = y(x),	x a,b ,

	x		y		dt.
x, y dS f x t , y t		2		2

	b
то f x, y dS f x, y x		1 y2	x	dx.
K	a

Допустим, что К имеет массу. Пусть ∆S – некоторая дуга кривой

содержащая точку М, а ∆m – масса этой дуги. Тогда отношение					m	S
средняя плотность ∆S, а	M	lim	m	- линейная плотность дуги в (∙)М.
		S M S

К,

-

Если μ = f(x,y) – рассматривать как линейную плотность дуги в текущей точке М(х,у), то dm = μdS – есть масса элементарной дуги ∆S и

интеграл

m

dS K

-масса линии – физический смысл криволинейного

интеграла I-го рода.

Свойства криволинейного интеграла I-го рода.

1)
K	K
2) K K1 K2			.
		K1 K2	K1 K2

Формула Грина.

Q

P

P x; y dx Q x; y dy

dxdy

D

x

y

,

P,Q – непрерывны вместе со своими частными производными.

Теорема: Криволинейный интеграл по дуге АВ не зависит от пути

интегрирования

интеграл по любому замкнутому контуру, проходящему

через (∙) А и В был равен 0.

Теорема: Пусть в области Д – односвязной заданы две функции P(x;y),

P

Q

Q(x;y) – непрерывны

- непрерывны в области D следующие

y

x

три утверждения эквивалентны:

1)

P x; y dx Q x; y dy 0, Д

2)

P x; y dx Q x; y dy dF x; y :

F x; y опред. в D:

dF P x; y dx Q x; y dy

3)

Q

P

.

x

y

Восстановление функции по её дифференциалу:

P

Q

P x, y dx Q x, y dy dF x, y

, F x, y ?

y

x

F x, y

B x, y

Pdx Qdy.

A x0 , y0

Таблица

1. Криволинейный интеграл 1-го рода.

	f(x,y)ds

2. Сведение К1. к определённому:

1)

y

f (x)

a x b

a

f(x,y)ds f (x, f (x)) 1 f 2 (x)dx

	b

2)x x(t), y y(t) t

f(x,y)ds f (x(t), y(t))	x2 (t) y 2 dt

3. Криволинейный интеграл 2-го рода.

P(x, y)dx Q(x, y)dy

l

4. Сведение К-2 к определённому:

1)	y	f (x)	x ,
P(x, y)dx Q(x, y)dy P(x, f (x)) Q(x, f (x)) f								(x)dx
l
2)	x	x(t), y y(t)		t ,
	P(x, y)dx Q(x, y)dy P(x(t), y(t))x (t) Q(x(t), y(t)) y (t) dx
5. Сведение К-2 к К-1:
P(x, y)dx Q(x, y)dy P(x, y)Cos (x, y) Q(x, y)Sin (x, y) ds
l					l
где		(x, y) - угол между направляющей касательной к
положительным направлением OX.
6. Формула Грина
					P(x, y)dx Q(x, y)dy		Q		P
							x		y	dxdy
				D		D

Практическая часть:

1. Вычислить криволинейный интеграл

(v)

и

Где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0) (рис. 43).

Поскольку

То остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА:

1)(АВ): так как уравнение прямой АВ имеет вид

Отсюда, учитывая, что х меняется от 0 до 1, получим:

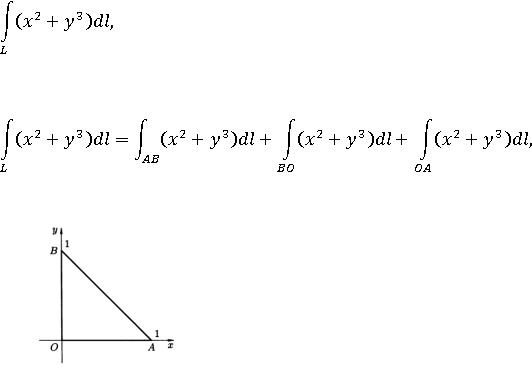
2) (ВО): рассуждая аналогично, находим

3) (OA):

.

4) Окончательно:

2. Вычислить криволинейный интеграл

Где L – окружность х2+у2=ах (а>0).
Введем	полярные	координаты		.	Тогда,
поскольку	х2+у2=r2,	уравнение	окружности	примет	вид
		а дифферинциал дуги
При этом		Следовательно,

3. Вычислить криволинейный интеграл первого рода от функции с тремя переменными

Где	L	–	дуга	кривой,	заданной	параметрически
				.

Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:

Теперь выразим через t дифферинциал dl:

Таким образом:

4. Показать, что интеграл

Не зависит от пути интегрирования, соединяющего точки (0,0) и

(10,10), и вычислить его.
Проверим условие Грина. Положим	Тогда

И значит, данный интеграл действительно не зависит от пути интегрирования. Для вычисления данного интеграла в качестве пути интегрирования возьмем простейший, т.е. отрезок, соединяющий точки О (0,0) и В (10,10). Отрезок ОВ можно задать так: При этом dy=dx, и интеграл легко сводится к определенному интегралу:

5. Проверить, является ли выражение

Полным дифферинциалом некоторой функции U(x,y) и если да, то

найти эту функцию.
Обозначим	Тогда

Таим образом, условие	Грина
имеет место при

Следовательно, данное выражение есть полный дифферинциал некоторой функции U(x,y), которая может быть найдена как криволинейный интеграл

Где (x0,y0) – произвольная фиксированная точка плоскости Оху, не лежащаяна оси Ох (так как ). П оложим (x0,y0)=(0,1), а в качестве пути интегрирования выберем путь L=ABC, изображенный на рис. 47. Тогда сокращенно можно написать:

Имеем:

1)(АВ):

2)(BC): х – фиксировано, следовательно, dx=0, откуда

3)Таким образом,

Проверка показывает, что действительно,

Задания для самосоятельного решения:

1. Вычислить

2.Вычислить

3.Вычислить

4.Проверить, что данный криволинейный интеграл не зависит от пути интегрирования и вычислить его:

5.Найти функции по данным полным дифферинциалам:

,

Положительные числовые ряды, признаки их сходимости

1.Числовые ряды, общий член ряда.

2.Положительные числовые ряды, достаточные признаки сходимости положительных рядов.

Теоретическая часть:

1. Числовые ряды. Основные понятия

Определение: пусть имеем {аn}- действительные числа

∞

Тогда выражение вида а1+а2+а3+….аn+…. – числовой ряд ∑ аn

n=1

а1, а2, а3,…., аn,…. – члены ряда; аn - общий член ряда.

S1= a1; S2 = a1+a2; S3 = a1+a2+a3; Sn = a1+a2+....+an = Sn-1 + аn .

Каждый ряд порождает последовательность частичных сумм. Определение: S = limSn (конечный или бесконечный ) называется

суммой ряда.

Определение: если S (-∞;+∞) , то ∑ аn- сходящийся; в противном случае расходящийся.

Свойства сходящихся числовых рядов

Определение: ряд, членами которого являются члены ряда (*)

а1+а2+а3+…+an+ ... an+k...+... , начиная с (n+1), взятые в том же порядке, что и в (*), называются n-ным остатком ряда (*). Обозначается Rn.

	∞
Теорема 1: ∑ an– сходится =>Rn – сходится, Ұ n.
	n=1
			∞
Теорема 2:			Rn – сходящийся =>∑an – cходится
			n=1
	∞		∞
Теорема 3:	∑an - сходится и ∑bn –сходится тогда:
∞n=1			n=1

∑( αan + βbn) –сходится

n=1

∞

Теорема 4:∑an - сходится => lim Rn= 0.

n=1

Теорема 5: ∑an - сходится => lim (Sn – Sn-1) = 0 <=> lim an = 0.

Ряды с положительными членами

Рассмотрим достаточные признаки сходимости положительных рядов:

Теорема 1:

∑an : аn≥0 и ∑bn : bn≥0; все an≤ bn

=> имеем: если

1). ∑bn - сходится => ∑аn - сходится.

2). ∑аn - расходится => ∑bn - расходится. Теорема 2: Предельная теорема сравнений.

∑аn и аn ≥0

Иlim(an/bn) = k =>

∑bn и bn≥0;

=>k	(0;+∞) и ∑аn- сходится	=> ∑bn- сходится
k	(0;+∞) и ∑bn- paсходится	∑аn- paсходится

То есть если k (0;+∞), то оба ряда ведут себя одинаково.

Таблица сходящихся и расходящихся положительных рядов.

Сходящиеся ряды

Расходящиеся ряды