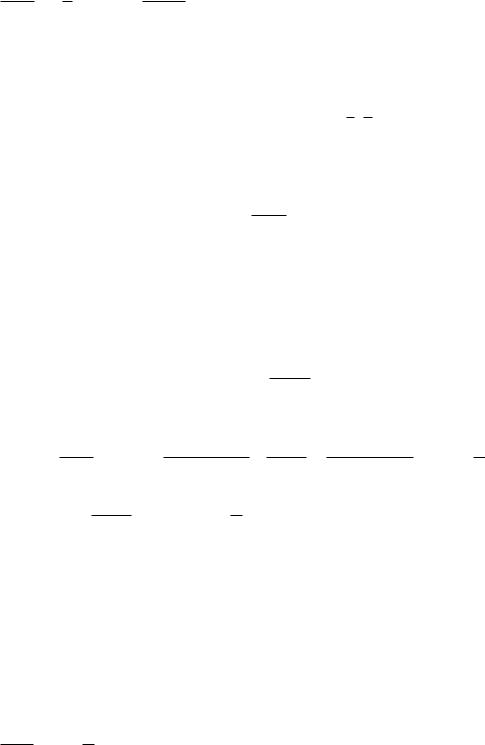Практикум по математическому анализу

ln c		n		1			1		1			... n					1		1		1		...
	n									2												2
				2		3n			4n								2		3n		4n
						1										1
lim		ln c					;	lim				c			e	2
			n			2							n
n									n
Известно, что ряд												1			сходится при s>1 и расходится при s 1.
												s
									n 1 n

Поэтому ряд

		2
	1
n 1	n

сходится. Применим предельный признак сравнения. Пусть

даны два ряда

а1+а2+а3 +…+ аn +…	(1)
b1+b2+b3 +…+ bn +…	(2)

lim n

a b

Тогда		если
n	k ,	то оба
n

существует конечный и отличный от нуля предел ряда (1) и (2) одновременно сходятся или одновременно

расходятся.

Положим

n 1

n

n

cn

n

1

1

a n

;

bn

, тогда

e

2

1

2

1

2

n

n

n

a

n

2

1

n

e

2

0.

lim

lim

c

n

2

n bn

n

n

1

Следовательно ряд сходится.

2. х=-1/е. Подставим в степенной ряд. Получим

		n 1			n	n
										n
			n				( 1)
			e					2	1		. Ряд из абсолютных величин членов этого ряда
							n
n 1

совпадает со сходящимся рядом, рассмотренным в пункте 1. Следовательно, он сходится и, причем, абсолютно.

Ответ: Область сходимости степенного ряда

2. Найти область сходимости степенного ряда.

		1	;	1
				.
		e
				e

		n
	5			n
			x		.
	n
n 1			1

Решение:

Радиус сходимости найдем по формуле

a

R

lim

n

.

n a n 1

5

n

5

n 1

a n

5

n

n 2

1

n 2

a n

; a n 1

;

n 1

n 1

n 2

a n 1

n 1

5

5 n 1

R

lim

a n

lim

1

n 2

1

n a n 1

n

5

n 1

5

Следовательно искомый предел равен

	R	1			1
сходимости			. Интервал сходимости			;
		5
					5

1/5.Таким образом радиус

1 . 5

Исследуем сходимость степенного ряда в концах интервала сходимости.

1. х=1/5. Подставим в ряд.

	5n			1	n			1
			.							. Ряд расходится как гармонический.
n 1							n 1
				5
n 1							n 1

2. х=-1/5. Подставим в степенной ряд. Получим

		n					n
	5				1
	n 1		.
n 1					5

n

( 1)n 1

n 1

.

Ряд

знакочередующийся. Так как

абсолютные величины членов этого ряда монотонно убывают и стремятся к нулю, то по признаку Лейбница ряд сходится.

Ответ: Область сходимости степенного ряда

3. Найти область сходимости степенного ряда.

		n
n
	x			.
n 1	2		n

Решение:

Радиус сходимости найдем по формуле

a

R

lim

n

.

n a n 1

1

1

a

a

n

; a

n 1

;

n

n

n 1

a n 1

2

n

2

(n 1)

R

lim

a

n

lim

2(1

1

) 2

n a n 1

n

n

	[	1	;	1	).
		5		5

2	n 1	(n 1)				1
				2(1			)
		n				n
	2		n

Следовательно искомый предел

сходимости	R 2	. Интервал сходимости

равен2; 2 .

2.Таким образом радиус

4. Исследуем сходимость степенного ряда в концах интервала сходимости.

1. х=2. Подставим в ряд.

n

n

1

2

.

2

n

n

Ряд расходится как гармонический.

n 1

n 1

2. х=-2. Подставим в степенной ряд. Получим

( 2)n

( 1)n

n

n

2 n

.

n 1

n 1

Ряд знакочередующийся. Так как абсолютные величины членов этого ряда монотонно убывают и стремятся к нулю, то по признаку Лейбница ряд сходится.

Ответ: Область сходимости степенного ряда [ 2; 2). 4. Найти область сходимости степенного ряда.

				n
			x
						.
			2n		3
		2				n
	n 1

Решение:

Радиус сходимости найдем по формуле

a

R

lim

n

.

n a n 1

1

1

a

n

1

2

2n 2 3

n 1

n 1

a

; a

;

3

n

2n

3

n 1

2n

2 3

2n

3

4

2

n

2

n 1

a n 1

2

n

1

n

R

lim

a

n

lim

3

n 1

4

4

n a n 1

n

n

Следовательно искомый предел сходимости R 4 . Интервал сходимости

равен 4.Таким образом радиус4; 4 .

Исследуем сходимость степенного ряда в концах интервала сходимости.

1. х=4. Подставим в ряд.

n

4

1

.

Ряд расходится как обобщенный

2n

3

3

n 1

2

n

n 1

n

гармонический при s=1/3<1.

2. х=-4. Подставим в степенной ряд. Получим

( 4)n

( 1)n

. Ряд знакочередующийся. Так как абсолютные

2n

3

3

n

n 1

2

n

n 1

величины членов этого ряда монотонно убывают и стремятся к нулю, то по признаку Лейбница ряд сходится.

Ответ: Область сходимости степенного ряда

[ 4; 4).

5. Вычислите определенный интеграл с точностью до 0,001, раскладывая подынтегральную функцию в ряд и затем интегрируя почленно.

0,5sin x dx.

0 х

Решение:

Разложим подынтегральное выражение в ряд. Воспользуемся табличным разложением

х

3

х

5

х

2n 1

sin х х

( 1)

n

3!

5!

(2n

1)!

Разделим обе части на x. Получим

sin x

x

2

x

4

x

2n

1

( 1)

n

х

3!

5!

(2n 1)!

Интегрируем это равенство от 0 до 0,5=1/2

0,5sin x

x 3

x 5

x 2n 1

1/ 2

dx

х

( 1)n

0

х

3! 3

5! 5

(2n 1)! (2n 1)

0

1

1

1

...

2

144

19200

Получили знакочередующийся ряд. Если мы ограничимся двумя

слагаемыми,

то ошибка

не превзойдет первого

отброшенного члена

1

0,001

19200

Поэтому с точностью до 0,001

	0,5	sin x		1		1
			dx				0,493
		х		2		144
	0

0,5sin x

Ответ: с точностью до 0,001 dx 0,493 .

0 х

6. Вычислите определенный интеграл с точностью до 0,001, раскладывая подынтегральную функцию в ряд и затем интегрируя почленно.

0,5х cos xdx.

0

Решение:

Разложим подынтегральное выражение в ряд. Воспользуемся табличным разложением

cos x 1	x 2		x 4	( 1)n	x 2n
2!		4!			(2n)!

Умножим обе части этого равенства на х. Получим

											x	3		x		5			x	2n 1
				х cos x х													( 1)	n
											2!				4!				(2n)!
	Интегрируем это равенство от 0 до 0,5=1/2
	0,5					x	2		x	4			x		6			x	2n 2			1
	хсosxdx																					2
													24				(2n)! (2n
	0					2		2			4					6					2)	0
		1		1				1
		8		128		9216
	Получили знакочередующийся ряд. Если мы ограничимся двумя
слагаемыми, то			ошибка					не		превзойдет первого отброшенного члена
1	0,001
9216

Поэтому с точностью до 0,001

	0,5	1			1
	xсosxdx					0,117
		8		128
	0

Ответ: с точностью до 0,001

0,5xсosxdx

0

Задания для самосоятельного решения:

0,117

.

1.Найти области сходимости ряда

2.Найти области сходимости ряда

3. Найти области сходимости ряда

Ряды Фурье. Разложение функций в ряд Фурье

1.Ортонормированные системы.

2.Коэффициенты, ряд Фурье.

3.Разложение четных и нечетных функций в ряд Фурье.

4. Разложение функции в ряд Фурье по «неправильному промежутку»

Теоретическая часть:

Определение:	f (x),

x [ ; ] интегрируема

ряд вида (2)

	a
		0	an	cos nx bn sin nx ,
	2
			n 1

где

1

1

a

f (x)dx

a

f (x)Cosnxdx

0

,

n

,

называется рядом Фурье функции f(x).

a

a

Если (2) – ряд Фурье f(x), то f(x) ~

0

2

n

n 1

			1
	1				f (x)Sinnxdx,
	b
	cos nx b				n	sin nx .

и

Заметим, что: ряд Фурье определен для любой интегрируемой функции на [ ; ]. Если этот ряд сходится то его сумма есть периодическая функция Т=2π. В этом смысле этот ряд естественно считать рядом Фурье для Т=2π – периодической функции которая получаеся из данной периодическим

продолжением с интервалом [ ;		] на R. В x=π она может быть задана
произведением, ряд Фурье от этого не меняется.
Определение:	f (x) x X	кусочно-монотонна
TX [ i i ]; [ i i ] f (x) - монотонна.
Ряды Фурье для чётных и нечётных функций
Лемма:	f (x), x [ l; l] чётная, интегрируемая (нечётная)

=>

l	l
	f (x)dx 2 f (x)dx
l	0

Рассмотрим чётную функцию

			2				2
	f (x), x [ ; ] a0			f (x)dx an				f (x)Cosnxdx bn= 0
				0				0	,
	Т.к. n f (x) Сosnx –чётная, а				f (x) Sinnxнечетная. => ряд Фурье для

чётной функции:

		a
	f (x) ~		0	anCos2nx
		2
				n1

По аналогии для нечётной функции ряд Фурье: а0=0; an=0;

			2
	bn			f (x)Sinnxdx
				0
					n
			f (x) ~		b Sin2nx
					n 1

Иногда требуется некоторую функцию f(x), определённую на [-π;0] или[0; π] разложить в ряд Фурье только по косинусам или только по синусам. Если данную функцию продолжить на [-π;π] чётным образом то по косинусам, если нечётным – то по синусам.

Разложение функций заданных на отрезке вида [а,а+2π]

Заметим, что любую 2 π периодическую функцию достаточно задать на некотором отрезке длины 2 π. В остальных точках она будет определена в силу периодичности. Найдём формулы, выражающие коэффициенты Фурье этой функции через её значения на произвольном отрезке длины 2π, т.е. на любом [а; а+2 π].

Лемма:f(x) – ограничена, периодична с периодом Т>0 и имеет конечное число точек разрыва на любом промежутке длины Т, то:

Т	а Т
f (x)dx	f (x)dx, x R.
0	0

Пусть f(x) – 2π-периодическая функция, а0, аn, bn – её коэффициенты Фурье. По лемме имеем: интеграл от f(x) по [а; а+2π] один и тот же , следоательно:

	* а0						1		а 2
									f (x)dx;
									а
				1		а 2
	an								f (x)Cosnxdx;
							а
			1			а 2
	bn								f (x)Sinnxdx; a R.
							а

Пусть на [а; а+2π] задана f(x). Продолжим её периодически с периодом 2π на все R (может быть для этого придётся изменить значение f(x) в одной или обеих точках а и а + 2π). Ряд Фурье полученной 2π-периодической функции называется рядом Фурье данной функции f(x), х [a; a 2 ] .

Ряды Фурье для периодических функций с произвольным периодом Т=2l, l>0

Любая периодическая функция f(x): Т=2l, l>0, заменой

	х	l	t

преобразуется в

φ(t)=f(

l

t

) cT=2π:

φ(t+2π)=f

(

l

(t 2 ))

=

f (

l

t 2l)

f (

l

t

Если

f (x), x [ l; l], l

0 (t) : t [ ; ]

a

(t) ~

0

an

cos nt bn

sin nt t

2

l

n 1

a

f (x) ~

0

an

cos n

x bn sin n

x

2

l

l

n 1

) (t).

x;
ряд Фурье для	f (x).

По аналогии имеем:

Теорема: Если 2l – периодическая функция f(x) ограничена и кусочномонотонна на [-l;l], l>0, то её ряд Фурье сходится к

f (x 0)	f (x 0)	, x R	(в	точке непр й	ряд сходится к	f (x)).
2

Практическая часть:

1. Разложить в ряд Фурье периодическую функцию f(x) с периодом 2π, заданную в интервале (-π;π) уравнением f(x)= π+x.

Графиком этой функции в интервале (-π;π) является отрезок, соединяющий точки (-π;0) и (-π;2π). На рис. 29 изображен график функции y=S(x), где S(x) – сумма ряда Фурье функции f(x). Эта сумма является периодической функцией с периодом 2π и совпадает с функцией f(x) на сегменте [-π;π].

Определим коэффициенты ряда Фурье. Сначала находим

		1		1			1
	a0		f (x)dx			( x)dx dx		xdx.

Второй интеграл равен нулю как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат. Таким образом

a0 dx 2 .

Далее, находим коэффициенты am . Имеем

Нетрудно видеть, что функция второго интеграла функции на нечетную). Итак,

Найдем коэффициенты

оба интеграла равны нулю (подынтегральная

является	нечетной	как произведение четной
am =0, т.е.	a1 a2 a3	... 0.
bm :

Первый интеграл равен нулю. Подынтегральная функция второго интеграла – четная как произведение двух нечетных функций. Таким образом,

Интегрируя по частям, получим u=x, dv=sinmx dx, du=dx, v= –(1/m) cos mx, т.е.

Следовательно, разложение функции f(x) в ряд Фурье имеет вид

2. Разложить в ряд Фурье периодическую функциюf(x) с периодом 2, заданную на сегменте [-1;1] уравнением f (x) x2 (рис. 30)