Практикум по математическому анализу

		(18x 4x							3	)(3		x			2	)	2	(9x		2	x	4	) 2(3			x			2	) 2x
y"
																	(3 x		2	)	4
	2x(3 x					2	)																								x(x		2	9)
									[(9 2x						2	)(3 x			2	)	18x			2	2x		4	]	6									.
	(3 x			2	)	4																									(3 x				2	)	3
у =0 при х=0, у не существует при х=																											3 .
		у
		-					+											-			+						-
											-1								0						1
(- ,-1) у 0, функция вогнута;
(-1, 0) у 0, функция выпукла;
(0, 1) у 0, функция вогнута;
(1,+ ) у 0, функция выпукла.
При х=0 имеем точку перегиба упер=у(0)=0.
6) Найдем наклонную асимптоту.
			y									x	2																			x		3						3x
k lim					lim											1;			b lim (y kx) lim																				lim			0
														2																						2	x				2
		x	x				x				3 x										x									x		3 x							x	3 x

Таким образом у=-х–наклонная асимптота. 7) Сделаем чертеж

						10					у
						9
						8
						7
						6
						5
						4
						3
						2
						1
7	6	5	4	3	2	1	0	1	2	3	4	5	6	7
						1
						2
						3
						4
						5
						6
						7
						8
						9
						10

х

Задания для самосоятельного решения:

Провести полное исследование функции и построить ее график

	x	2	x 6
y				.
			x 2

Исследование функции и построение схемы ее графика

1.Полное исследование функции.

2.Построение схемы графика функции.

Теоретическая часть:

Общая схема исследования функции и построения ее графика

I. Элементарное исследование: 5)найти область определения функции;

6)исследовать функцию на четность (нечетность);

7)исследовать функцию на периодичность; 8)определить, если это не вызовет особых затруднений, точки пересечения графика с координатными осями.

II. Исследование графика функции по первой производной: 7)найти у'(х);

8)используя необходимый признак существования экстремума найти точки, «подозрительные» на экстремум, т.е. точки в которых у'(х)=0 или у′(х) не существует; 9)нанести критические точки на область определения и найти знак про-

изводной во всех получившихся интервалах; 10)используя признаки монотонности определить характер монотонности функции на каждом интервале;

11)используя достаточный признак существования экстремума установить наличие экстремума и их характер; 12)вычислить значение функции в точках экстремума, если они есть.

III.Исследование графика функции по второй производной:

1)найти у" (х);

5)используя необходимый признак существования точек перегиба, найти точки «подозрительные» на перегиб, т.е. точки в которых у"(х)=0 или у"(х) не существует;

6)нанести полученные точки на область определения и найти знак второй производной в каждом из получившихся интервалов;

7)используя теорему о форме кривой установить характер выпуклости (вогнутости) графика функции на каждом промежутке;

7)используя достаточный признак существования точек перегиба установить их наличие;

8)вычислить значения функции в абсциссах точек перегиба.

VII.Исследовать поведение функции на границах области определения.

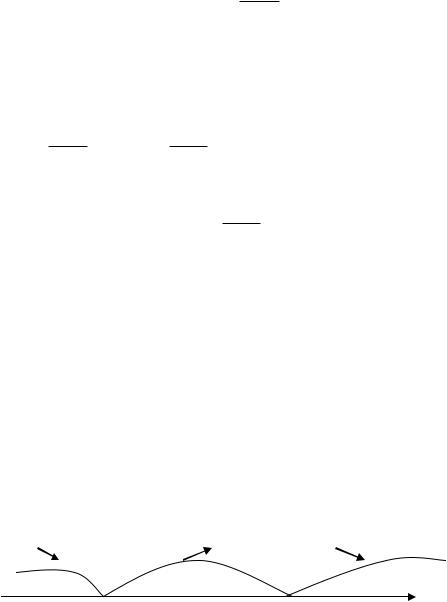
VIII.Исследовать кривую y=f(x)на наличие асимптот и указать область значений функции.

IX.Построить график функции.

Если исследование произведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить ошибки.

Практическая часть:

1. Провести полное исследование функции и построить ее график

а)

x 2		2
y	.
x 2

Решение 1) Область определения функции х(-,2)(2,).Функция

непрерывна в области определения, х=2–точка разрыва. Найдем односторонние пределы

x 2

2

x 2

2

lim

lim

.

Следовательно,

x 2 0

x 2

x 2 0

x 2

х=2–вертикальная асимптота.

x 2

2

x 2

2

y(x)

2)

y( x)

.

x 2

x 2

Следовательно, функция общего вида.

3)Найдем точки пересечения с осями.

Сосью Ох. у=0 х=-2.

Сосью Оу. х=0 у=1.

у 0 при всех х, кроме х=-2.

4) Исследуем функцию на возрастание, убывание, точки экстремума.

x 2

x 2

'

x 2

1 (x 2) (x 2) 1

y' 2

2

8

(x 2)2

x 2

x 2

x 2

	x 2	.
	(x 2)3

y=0 при х=-2; у не существует при х=2. у

-	+	-
-2	0	2

Таким образом (-,-2) у 0, функция убывает;

(-2,2) у 0, функция возрастает;

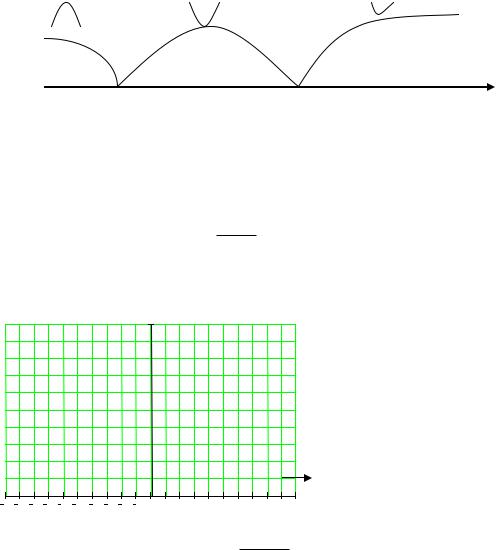
(2,+) у 0, функция убывает.

Точка х=-2–точка минимума, так как производная меняет знак с

минуса на плюс. уmin=0.

5) Исследуем функцию на выпуклость, вогнутость, точки перегиба

y" 8	(x 2)3	(x 2) 3(x 2)2	8	x 2 3x 6		16	x 4		.
		(x 2)6		(x	2)4		(x 2)	4

у =0 при х=-4, у не существует при х=2.

у
-	+	+
-4	0	2

(-,-4) у 0, функция выпукла; (-4, 2) у 0, функция вогнута; (2,+) у 0, функция вогнута.

При х=-4 имеем точку перегиба упер=у(-4)=(-2/-6)2=1/9.

6) Так как

lim y lim
x	x

 

x x



2		2
2

=1, то у=1–горизонтальная

асимптота (частный случай наклонной). 7) Сделаем чертеж

10 9 8 7 6 5 4 3 2 1

у

х

20

18

16

14

12

10

8

6

4

2

0

2

4

6

б)

8	10	12	14		16		18	20
				x		3
y								.
		x		2		1

Решение 1)Область определения функции х(-,-1)(-1,1) (1,).Функция

непрерывна в области определения, х=-1 и х=1–точки разрыва. Найдем односторонние пределы

x3

x3

x3

x3

lim

. , lim

. , lim

. , lim

. .

x 1 0 x 2 1

x 1 0 x 2 1

x 1 0 x 2 1

x 1 0 x 2

1

Следовательно х=-1 и х=1–вертикальные асимптоты.

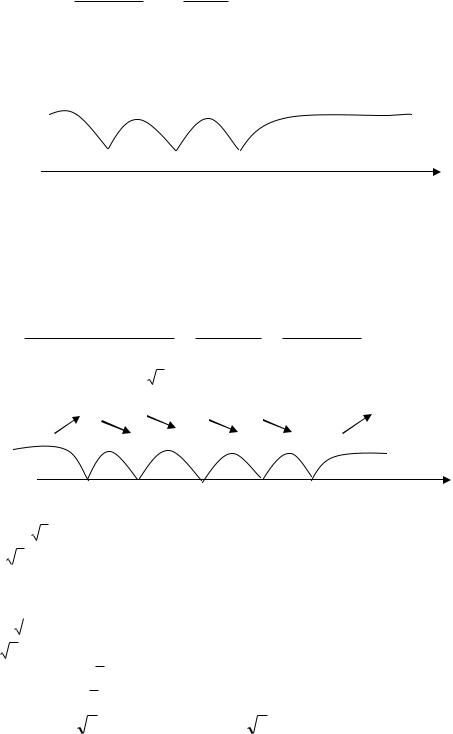
2)	y( x)

( x)
		3
( x)	2	1	.

		x	3
		2
	x		1

y(x)

.

Следовательно функция нечетная. 3) Точка пересечения с осями (0,0).

	y
-	+	-		+
	-1	0	1	x

Винтервале (-;-1) у<0;

Винтервале (-1;0) у>0;

Винтервале (0;1) у<0;

Винтервале (1;+ ) у>0;

4)Исследуем функцию на возрастание, убывание, точки экстремума.

		3x		2	(x	2	1)			x		3	2x		x	4	3x		2		x	2	(x		2	3)
y'																												.
					(x			2		1)	2				(x		2	1)	2		(x			2	1)		2
y=0 при х=0 и х=													3 1,7				, у не существует при х=1.
у
				+					-				-					-			-						+
											-1,7			-1						0						1		1,7
Таким образом
(-,- 3 ) у >0, функция возрастает;
(- 3 ,-1) у 0, функция убывает;
(-1,0) у 0, функция убывает;
(0,1) у 0, функция убывает;
(1,			) у 0, функция убывает;
		3
( 3	,) у >0, функция возрастает;

Вточке х=- 3 функция имеет максимум.

Вточке х= 3 функция имеет минимум.

ymax	3	3	2,6;	ymin	3	3	2,6
		2				2

5)Исследуем функцию на выпуклость, вогнутость, точки перегиба

	y"		(4x3 6x)(x 2		1)2 (x 4 3x 2 ) 2(x 2 1) 2x
					(x 2 1)4
		2x(x 2 1)		[(2x 2	3)(x 2 1) 2(x 4 3x 2 )]		2x		(x 2	3)
		(x 2 1)4				(x	2	1)3

у =0 при х=0, у не существует при х=1.

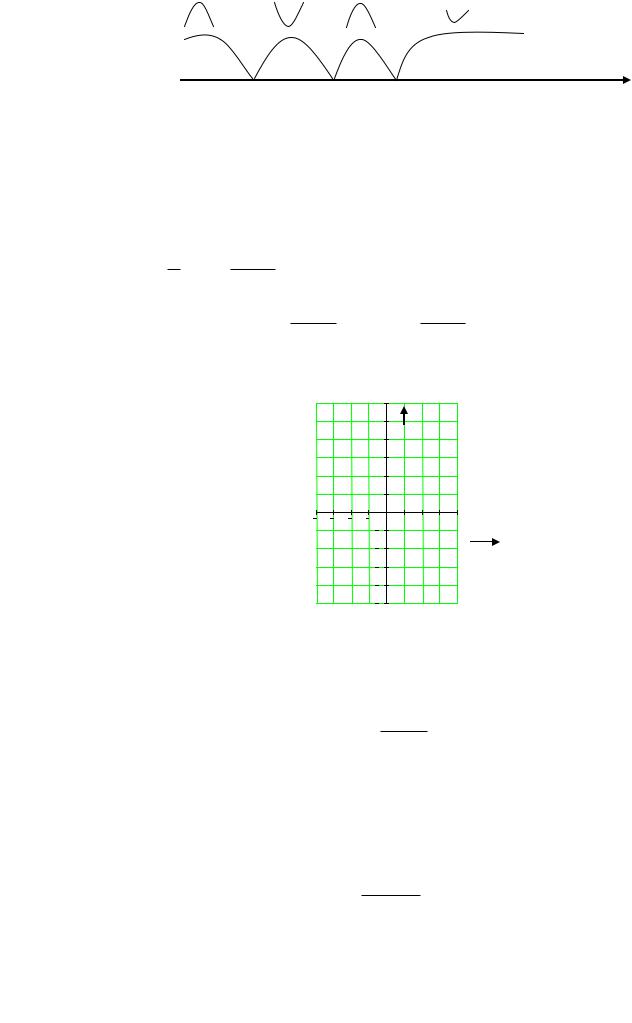
у
		-			+			-			+
						-1		0		1
(-,-1) у 0, функция выпукла;
(-1, 0) у 0, функция вогнута;
(0, 1) у 0, функция выпукла;
(1,+) у 0, функция вогнута.
При х=0 имеем точку перегиба упер=у(0)=0.
6) Найдем наклонную асимптоту
	y		x	2
k lim		lim		1;
			2
x x		x x		1
						x	3			x
b lim ( y kx) lim (								x) lim			0
						2	1		2	1
x				x	x			x x

Следовательно у=х–наклонная асимптота. 7) Сделаем чертеж:

				6			у
				5
				4
				3
				2
				1
4	3	2	1	0	1	2	3	4
				1
				2
				3
				4
				5

х

Решите самостоятельно:

Исследуйте функцию методами дифференциального исчисления и постройте ее график.

	y	12x		.
		9 x	2

Задания для самосоятельного решения:

Исследуйте функцию методами дифференциального исчисления и постройте ее график

2x 2

y 4х 2 1.

Задачи на экстремум

Практическая часть:

1. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объема V. Каковы должны быть высота ведра и радиус его дна, чтобы на его изготовление ушло наименьшее количество жести?

Решение

Обозначим:
h-высота ведра;
r-радиус дна.
Сделаем чертеж	h

По условию

V= r2h (1) 2r

Полная поверхность

S=Sосн+Sбок= r2+2 rh (2)

Выразим h из уравнения (1) h=V/ r2

и подставим в (2). Получим

	S= r2+	2V	.
		r

Таким образом, получили функцию от r. Исследуем эту функцию при

dS

2 r

2V

0;

dr

r

2

2

r

3

V ;

d

S

4V

r (0, ).

2

0 при

r (0, ),

Так как

2

3

то

dr

r

V

r

3

.

функция имеет в данной точке минимум. При этом

2

V

V

V

V

h

3

2 3

( r) .Таким образом, у ведра

r

2

V

V

2

3

2

оптимальных размеров h=r= 3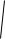 V .

2. Найти наименьшее и наибольшее значения функции на отрезке

	y 4 x	4		[1;4]
		x	2

Решение

1. Находим производную

	y' 1	8		.
		x	3

2. Находим критические точки Производная равна нулю

	1			8		0.
				x	3
	x
		3	8
	x 2 [1;4]

Производная не существует при х=0 [1;4]

3.Находим значения функции в точках х=1, х=2, х=4.

у(1)=4-1-4=-1; у(2)=4-2-1=1; у(4)=4-4-1/4=-0,25.

4.Выбираем наименьшее и наибольшее значения

унаим=у(1)=-1, унаиб=у(2)=1.

Ответ: унаим=у(1)=-1, унаиб=у(2)=1.

3.Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?

Решение

Сделаем чертеж

h 2r

Для того, чтобы окно пропускало наибольшее количество света, нужно сделать площадь окна максимальной. Выразим площадь окна через h и r.

S=2 h r+ r2/2

По условию известен периметр

P=2h+2r+ r=a

Отсюда

h= a r 2r

2

Подставляя в выражение для площади, получим

				(4 )r	2
	S=(a-r-2r)r+ r2/2=ar-2r2-r2/2=ar-(2+ /2)r2=ar-				.
				2
	Исследуем эту функцию при r[0,	а	]. (При больших значениях
		2
	получим h<0).

							dS		a (4 )r 0;
							dr
						r					a		.
										4
Вычислим значения S в точках r=0,															a		,		a
														4				2
S(0)=0;			a
	a				(4 )			a	2					a	2					1		a	2
S(		)=a		-												(1					)			0,07a	2	.
											2
	4		4					)						)								2(4 )
					2	(4						(4								2

r

	S(	a
	2
	a
	2



)=a

4		a	2			a	2				a
											2
									(4	2 4 )				0,059a	2
2		(2 )		2		2(2 )		2			2(2 )		2

	Таким образом наибольшее значение площади получится при r=										a
										4
	при этом h=	a (2 )r		a	(1		2	)	a	. Таким образом ширина
		2		2			4		4

оптимального окна (2r) в два раза больше высоты.

Задания для самосоятельного решения:

1. Найти производные заданных функций:

,

						5	25 x2
	1) y arctg	x2 4	2)	y e3x 2xtg 2 3x 3)	y ln
							x

2.Вычислить приближенное значение 4,0021/2

3.Найти полный дифференциал функции z=(2x-y)cos(3x+2y)

4. а) Провести полное исследование функции её график.

3	х	2
у х 3

и построить

б) Провести полное исследование функции у=х3+3х2+3 и построить её график. Составить уравнение касательной и нормали, проведенной к графику функции в точке х0=1.

Функция двух переменных, ее дифференцирование

1.ОДЗ функции двух переменных.

2. Частные и полное приращение функции двух переменных.

3.Частные производные функции двух переменных, ее дифференциал первого порядка

Теоретическая часть:

Определение: Отображение f некоторого подмножества Df двумерного евклидового пространства R2 во множество R называют действительной функцией 2-х действительных переменных.

Df называют областью определения функции f.

Так как Df R2 , то геометрическим образом Df явл множество точек плоскости.

Обозначение: f: Df R или f: (x,y) z или z=f(x,y), где (x,y) Df, а z R. (х,у) – значение аргумента, z – значение функции.

Пусть при f: (х0,у0) z0 , тогда (z0) называют значением f в точке (х0,у0)

и пишут: z0=f(х0,у0).

Определение: Множество всех значений функции называется множеством значений функции и обозначают Ef = {z R| z=f(x,y), где

(x,y) Df}.
Определение: Графиком функции z=f(x,y)	двух переменных,

определенной на множестве Df называется множество Гf = {(x,y,z) R3 | z=f(x,y)где (х,у) Df}.

Геометрически: Гf – множество точек 3-х мерного пространства.

Предел и непрерывность функции 2-х переменных Определение: Пусть Р0(х0,у0) – предельная точка Df функции z=f(x,y).

Число А наз пределом функции z= f(x,y) в точке Р0(х0,у0) (или при х х0, у у0), если (>0)( >0)( (x,y) Df | (x,y) (х0,у0) ^ |x-х0|< ^ |y-y0|< ) |f(x,y)-A|< .

Для предела функции 2-х переменных справедливы аналоги теорем о пределе суммы, произведения и частного 2-х функций.

Определение: Функция 2-х переменных z=f(x,y) наз непрерывной в точке Р0(х0,у0), если предел этой функции в точке Р0 равен её значению в этой точке.

Определение: Пусть z=f(x,y) определена в некоторой окрестности точки Р0(х0,у0), тогда разнность z=f(х0+ x, y+у0)-f (х0,у0) называется полным приращением функции.

Определение: z=f(x,y) называется непрерывной в точке Р0(х0,у0), если бесконечно малым приращениям аргумента x и у соответствует бесконечно малое приращение функции.

Для функции 2-х переменных справедливы аналоги теорем о непрерывности суммы, произведения, частного функций, сложной функции и др.

Частные производные