Бакаев Методы статистических испытаний 2007

Глава 6 Анализ непрерывного потока финансовых платежей

В рамках финансово-инвестиционного анализа приходится вычислять так называемую чистую приведенную стоимость или NPV (Net Present Value) потока финансовых платежей, которая в случае непрерывного потока платежей вычисляется по формуле (см., например, [15]):

NPV = ∫0T e −r t ρ(t)dt ,

(6.1)

где e −r t – значение коэффициента дисконтирования для промежутка времени [0;t]; r – (постоянная) банковская ставка; ρ(t)– функция интенсивности (плотности) платежей;

T –период наблюдения.

Таким образом, данная практическая задача сводится к вычислению интеграла, и в данной главе будет рассмотрено, как можно решить ее, применяя методы статистического моделирования. Но вначале целесообразно обсудить возможности применения методов Монте-Карло для вычисления интегралов произвольного вида, поскольку в такой общей постановке задача интегрирования имеет самостоятельный интерес и возникает в других финансовоэкономических приложениях. После этого можно будет вернуться к проблеме вычисления интеграла (6.1).

6.1 Необходимые сведения из математической статистики

Ранее уже упоминалось, что очень многие задачи, решаемые методами Монте-Карло, в частности те, что связаны с вычислением, могут быть интерпретированы как вычисление математического ожидания некоторой случайной величины. Ниже будет приведен необходимый для последующего изложения набор сведений, касающийся

121

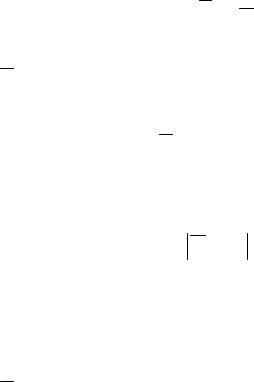
статистических оценок величины математического ожидания.

Предположим, что поставлена задача оценки математического ожидания а для некоторой одномерной случайной величины Х, то есть следует оценить величину

a = M[X ].

Если при этом имеется в распоряжении некоторый набор (выборка) Х1,Х2,…,ХN из N независимых реализаций случайной величины Х, то в качестве оценки математического ожидания в математической статистике принимается среднее арифметическое

X N := 1 ∑N Xi .

N i=1

Согласно закону больших чисел (теорема Хинчина) величина

X N сходится по вероятности при N → ∞ к математическому ожиданию а случайной величины Х, то есть

P

X N → a, N → ∞ .

Это означает (см., например, [13 , глава 20]), что при любом фиксированном ε > 0

lim P ( X n − a > ε)= 0 .

N → ∞

Проведенное рассуждение дает основание считать, что при больших N выполняется приближенное соотношение

				X	N	≈ a ,
и,	таким	образом,	за			приближенное			значение
(статистическую оценку)			величины				а	можно принять

X N .

122

σ 2 = D[X ]= M[X 2 ]− (M[X ])2

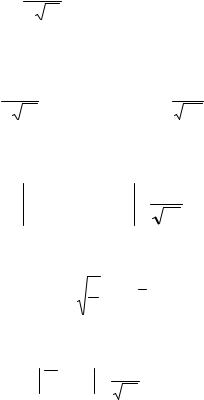
Для определения погрешности полученной оценки предположим, что случайная величина Х имеет конечную дисперсию

.

Согласно центральной предельной теореме, последовательность одинаково распределенных независимых

случайных величин с конечной дисперсией σ 2 порождает случайную величину

1	N	a = M[X ],
	∑(Xi − a),
σ N	i =1

которая в пределе при N → ∞ нормально распределена с параметрами (0,1). Более точно,

				1	N	(Xi − a)<x2
lim			<		∑				=
	P	x1		σ N
N →∞					i =1

Принимая далее x2 = −x1 = x, получим

			1	N	(X		− a ) < x σ
lim	P			∑
						i
N → ∞			N				N
				i =1

1	x 2	e	−t2	dt .
			2
2π ∫x1

= Φ(x ),

где Φ(x) – интеграл вероятностей:

Φ(x)=	π2	∫0x	e−	t2
				2 dt .	(6.2)

Поэтому при больших N можно принять

P

	xσ		≈Φ(x).
X N − a <
	N

В этой приближенной формуле x ≥ 0 можно фиксировать произвольным образом. В частности, задавая доверительную

123

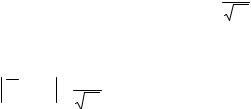
вероятность β и	обозначая через xβ	корень уравнения
Φ(x)= β , можно	оценить вероятность	того, что ошибка

приближения			X	N − a		меньше		величины
определяется величиной β , то есть
							xβ σ
				X N − a		<		≈ β .
	P
							N

xβ σ	и
N

(6.3)

Чаще всего берут β = 0.977, тогда xβ = 3, или β = 0.95, тогда xβ = 1.96.

Трудно, конечно, представить себе задачи, в которых
требовалось бы определить		M[X ]	(то есть			M[X ]	была бы
неизвестна) при известной дисперсии					D[X ]. Поэтому на
практике используют приближенную формулу
σ 2 ≈ sN2 : =	1	N	1		N	2
		∑ X i2	−		∑ Xi .
	N i =1		N i =1

Из математической статистики известно, что это – смещенная статистическая оценка для дисперсии. Но при больших N , а именно при таких N имеет смысл построенная выше приближенная оценка для M[X ], смещенная оценка

для дисперсии мало отличается от несмещенной. Существуют также методы оценки ошибки, не

использующие значения дисперсии или оценки дисперсии, а также методы оценки ошибки в задачах с бесконечной дисперсией. За деталями заинтересованный читатель может обратиться к книге [10].

124

6.2 Простейший метод Монте-Карло для вычисления интегралов

Теперь обсудим вопрос, каким образом применение техники Монте-Карло позволяет решать задачу вычисления интеграла – задачу чисто детерминированную. Итак, пусть требуется вычислить интеграл

Ι = ∫D f (x)p(x)dx = ∫ f (x1,x2,...,xn )p(x1,x2,...,xn )dx1 dx2 d xn ,

D			(6.4)
где D – заданная	область	n-мерного1, 2 ,…,xпространстваn		;
x = (x1;x2;...;xn ) – вектор переменных x x			;
f (x)= f (x1,x2,...,xn ) –	заданная	функция	n переменных;
p(x)= p(x1 ,x2 ,...,xn ) – плотность распределения некоторой
n-мерной случайной величины Х, причем			p (x)>0 при x D

(очевидно, такие случайные величины всегда существуют). Тогда исходный интеграл легко преобразуется к виду (6.4) следующим приемом:

				∫D f (x)dx = ∫D f1(x)p(x)dx ,	(6.5)
	где f1(x)=	f (x)		. В частности, если область	D имеет
		p(x)

конечный объем (объем D < ∞), то можно принять в (6.5)

p(x)≡	1	– плотность равномерно распределенной в D
	объем D

случайной величины.

Итак, без ограничения общности, будем рассматривать задачу вычисления интеграла в форме (6.4), где p(x) –

плотность распределения n-мерной случайной величины Х, принимающей свои значения в области D.

Введем далее одномерную случайную величину Y := f (X), для которой

125

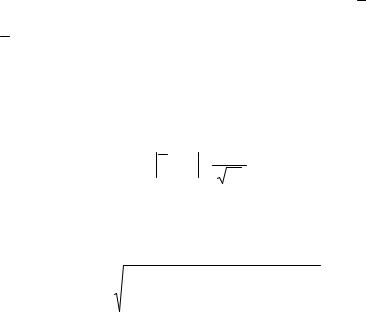
M[Y ]= ∫D f (x)p(x)dx = Ι .

Опираясь теперь на тот факт, что значение I искомого интеграла на самом деле совпадает с математическим ожиданием одномерной случайной величины Y, воспользуемся техникой построения статистических оценок (необходимая сводка результатов приведена в предыдущем параграфе книги).

Опишем теперь процедуру применения простейшего метода Монте-Карло. Пусть X1,X2,...,XN – независимые реализации случайной величины Х. Поскольку плотность распределения p(x) случайной величины Х известна, для

генерации X1,X2,...,XN можно применять методику, описанную в параграфе 4.3. Тогда в качестве оценки интеграла (6.4) можно принять

Y N =		1 ∑Yi =		1 ∑ f (Xi ).
			N		N
		N	i =1	N	i =1

При этом, как следует из теории вероятностей, M[Y N ]= Ι и

P

Y N →Ι при N → ∞ .

Оценка погрешности полученной оценки производится

так же, как описано в параграфе 6.1, а именно, задаваясь
некоторой	доверительной	вероятностью	β (0;1),

принимаем, пользуясь центральной предельной теоремой,

			xβ sN
	Y N −Ι	<
P			N

	≈ β ,	(6.6)

где sN – оценка среднего квадратичного отклонения случайной величины YN , которую можно, например, принять в виде

1

N

2

1

N

2

S

=

∑

(f (X

))

−

∑ f (X ) .

N

N i =1

i

N i=1

i

Замечание 6.1. Существует большое число различных модификаций указанного выше метода Монте-Карло,

126

которые могут приводить при одном и том же N к различным оценкам для SN и, значит, к различным

интервалам допустимого разброса значений искомого интеграла. Однако на практике приходится также учитывать трудоемкость каждого такого метода, которая в основном связана с трудоемкостью генерации нужных случайных величин. Встречаются ситуации, когда, например, из двух сравниваемых методов тот метод, который обладает худшей дисперсией (при фиксированном N), характеризуется в то же время меньшей трудоемкостью, и за счет применения его при большем N, чем для метода с лучшей дисперсией, такой метод оказывается в конечном счете более эффективным. Конкретные примеры такого рода могут быть найдены в книге [18, глава 3].

6.3 Финансовые платежи

Вернемся к проблеме анализа потока финансовых платежей, которая, как уже было указано ранее, сводится к задаче вычисления интеграла (6.1). Применим для решения этой задачи простейший метод Монте-Карло. Для удобства

введем нормированное время x := Tt . Тогда вместо (6.1)

получим

	NPV = ∫01 e −r T x ρ(T x)T dx = 1− er −r T					∫01 ρT (x) p(x)dx , (6.7)
	где	(x) : = ρ(T x),	p(x) : =			rT	e −r T x
	ρ
				1		− e −r T
	T

(очевидно, что ∫01 p(x)dx =1).

127

Далее, пусть x1,x2,...,xN – независимые реализации случайной величины Х, распределенной с плотностью p(x). Тогда, согласно методике, описанной в параграфе 6.2, имеем следующую оценку Монте-Карло для NPV:

		−r T	N
NPV N = 1− e			∑	ρ	(x ) .	(6.8)
	r N		i =1	T	i

Поскольку большинство генераторов выдают обычно случайные числа, распределенные равномерно в (0;1), для генерации случайной величины Х применим метод обратных функций. Вычислим сначала функцию распределения F(x), соответствующую плотности p(x):

0,

x ≤0 ,

F(x)= ∫

x

1− e −r T x

, 0

<x <1 ,

−∞

ρ(y)dy =

− e −r T

1

1,

x≥1 .

Поэтому, удобно моделировать

реализации γ1,γ2,...,γN

случайного числа Г и использовать связь

1− e −r T X

= Γ

1− e −r T

или

1

1

X =

ln

rT

1− (1− e −r T )Γ

128

Таким образом, реальная практическая схема построения оценки Монте-Карло для NPV основывается на применении формулы (6.8), где

1		1
xi: = r	ln	1− (1− e −r T )γi	.

Для того чтобы указать погрешность оценки (6.8), что эквивалентно построению соответствующей интервальной оценки, вычислим статистическую оценку среднего квадратичного отклонения

2

1

1

− e −r T

1

N

2

1

N

2

s

=

r

∑

ρ

(x

)−

∑

ρ

(x

)

.

N

N i =1

T

i

N i =1

T

i

Задаваясь

некоторой

доверительной

вероятностью

β (0;1), интервальная оценка принимается приближенно в виде (6.6), в которой Y N и I заменены, соответственно, на

NPV N и NPV.

129

Глава 7 Механические торговые системы

Механические торговые системы применяются при использовании активного управления инвестиционным портфелем. По сути дела механическая торговая система

(или, сокращенно МТС) – это набор правил, жестко регламентирующих моменты открытия и закрытия позиций; другими словами, МТС задает правила входа в позицию или выхода из позиции в зависимости от складывающейся ситуации. Для получения доходов от операций с ценными бумагами трейдер должен ещё иметь в распоряжении набор правил для управления капиталом. Эти правила должны определять объем открываемых позиций в момент поступления соответствующих сигналов от МТС. В отличие от интуитивного подхода в торговле использование механических торговых систем позволяет полностью исключить эмоциональный фактор при принятии торговых решений и, как следствие, применять научно обоснованные статистические методы для исследования результатов работы МТС.

Поскольку правила, определяющие работу МТС, обычно разрабатываются на основе анализа исторических временных рядов цен активов, нельзя представить абсолютную гарантию, что МТС, построенная на таком ретроспективном анализе, будет успешно работать в будущем. Однако чем более качественно проведено тестирование МТС, тем больше имеется оснований рассчитывать на то, что результаты ее работы будут приводить к удовлетворительным для трейдера доходам и в будущем.

Успех работы любой МТС существенно зависит от того, насколько успешно выбраны ее параметры – так называются переменные, фигурирующие в правилах открытия и закрытия позиций. В результате тестирования МТС и последующей ее оптимизации определяется набор параметров, при которых важнейшие показатели системы находятся в оптимальных для данного трейдера пределах. Как правило, МТС создается,

130