Бакаев Методы статистических испытаний 2007

Из сравнения двух выражений для F(х) легко получить, что

c1 = c2 = 1 . Итак, моделирование проводится по схеме:

2

а) сначала моделируется значение k, при этом

	1		,	если	Г1	≤ c1
	k =	2,		если	Г	> c .
					1	1

б) затем моделируется сама случайная величина Х по формуле

1

Х = (Г2)к(k +1 ) .

Применение метода суперпозиции для повышения эффективности вычислительных алгоритмов моделирования

В качестве одного из полезных приложений метода суперпозиции рассмотрим вопрос о возможном повышении эффективности вычислительного процесса моделирования искомой случайной величины за счет аппроксимации ее плотности распределения другой, близкой к ней и в каком-то смысле более простой плотностью распределения и дальнейшего учета поправок к такой аппроксимации.

А именно будем предполагать, что плотность распределения p(x) (для простоты, одномерной) случайной величины Х, принимающей свои значения на интервале (а; b), может быть хорошо аппроксимирована некоторой функцией q(х), такой, что p(x) ≥ q(x) при x (a;b). Функция q(х), сама не обязана являться плотностью распределения, но функция

p1(x) :=	1	q (x), где	с := ∫ab q(x) d x ,
	c1		1
			81

уже будет плотностью распределения некоторой новой случайной величины, принимающей значения в том же интервале (а ; b). Заметим, что ввиду наложенного выше неравенства между p(x) и q(x) обязательно должно выполняться c1 [0;1]. Исключая из дальнейшего рассмотрения

тривиальные частные случаи,	когда с1 = 0 и c2 = 1,	будем
считать, что c1 (0;1).
Представим теперь p(x)	в виде суперпозиции	двух

плотностей p(x) = c1 p1(x) + c2 p2(x) , где с1 и p1(х) были уже определены выше, а кроме того, c2 = 1 – c1 и

p2 (x) := 1 ( p( x) − q(x)). c2

При этом элементарно проверяется, что p2(х) играет роль плотности для некоторой непрерывной случайной величины, принимающей значения в интервале (0; 1). По плотностям р(х), p1(х) и p2(х) можно восстановить соответствующие функции распределения F(х), F1(х) и F2(x), для которых естественно должно иметь место равенство

F(x) = c1F1(x) + c2 F2 (x).

Последнее соотношение может быть теперь взято за основу для моделирования при помощи метода суперпозиции. Обсудим, однако, какие преимущества может принести применение метода суперпозиции в данной ситуации. Прежде всего, так как по предположению функция q(х) достаточно близка к р(х) , следует ожидать, что величина с1 будет весьма близка к 1, а величина с2, соответственно, будет весьма мала.

82

Следовательно, алгоритм, построенный на применении метода суперпозиции, будет существенную часть своего вычислительного времени тратить на обращение к процедуре обращения функции F1(х), которая по нашим предположениям имеет простую структуру, а это должно привести к существенной экономии вычислительных затрат. Что же касается процедуры обращения функции F2(х), то ввиду малости c2 эта процедура, хотя сама по себе и трудоемкая, будет крайне редко использоваться в процессе счета и практически не скажется на увеличении всего алгоритма в целом.

83

Глава 5 Стохастические дифференциальные уравнения

Адекватное описание многих развивающихся во времени финансово-экономических процессов связано с использованием аппарата стохастических дифференциальных уравнений. В настоящей главе рассмотриваются на элементарном уровне некоторые вопросы теории таких уравнений, а также вопросы их численного решения (моделирования).

5.1 Дельта-функция

Изложение в данной главе начинается с более или менее популярного обсуждения понятия и простейших свойств дельта-функции δ(t), использование которой потребуется для характеризации некоторых случайных процессов специального вида. Прежде всего отметим, что дельта-функция не является функцией в привычном смысле, то есть не может быть представлена как закон соответствия между поточечными значениями независимой и зависимой переменных, как это делается при определении функции в курсе математического анализа.1 На самом деле дельта-функция принадлежит классу так называемых обобщенных функций, элементы которого называются функциями только в силу определенных терминологических традиций, а на самом деле таковыми в указанном выше привычном смысле не являются.2 Более

1Отметим, что в некоторых физических курсах делаются попытки объяснения дельта-функции именно путем ее задания на основе такого соответствия (см., например, А. А. Соколов, И. М. Тернов, В. Ч. Жуковский, Квантовая механика, М.: Наука, 1979, с. 49-55), в частности, выписываются формулы типа приведенной ниже формулы (5.4), что с нашей точки зрения не только не облегчает, а делает еще более неясным комментарий этой функции.

2 В теории обобщенных функций показывается, что обобщенным функциям, в частности дельта-функции, можно приписать числовые значения при определенных значениях независимого аргумента, но, к сожалению, не для всех.

84

правильно было бы называть их (как это часто и делается) функционалами или мерами. Строгий подход к изучению дельта-функции требует привлечения серьезного математического аппарата, изложение которого в рамках данной книги не представляется возможным. Поэтому приходится ограничиться некоторыми не совсем строгими рассуждениями, которые, как предполагается, будут достаточны для формирования соответствующих понятийных представлений у читателя, не владеющего глубокой математической подготовкой, но стремящегося применять аппарат случайных процессов и стохастических дифференциальных уравнений в прикладных финансовоэкономических исследованиях.

Будем исходить из следующего не вполне строгого определения дельта-функции.

Определение 5.1. Дельта-функция δ(t) определяется условием

∫−∞∞ δ(t) f (t) dt = f (0)

(5.1)

для любой непрерывной функции f(t), t (− ∞;∞)‚ где интеграл

понимается в некотором более общем смысле, чем интеграл Римана.

Нестрогость данного определения как раз и заключается в неопределенности смысла, который придается возникающему в контексте интегралу. Заметим, что невозможно использовать здесь понятие интеграла Римана по той причине, что дельтафункция не является, как было сказано, обычной функцией, а это, в частности, приводит к тому, что интеграл Римана с дельта-функцией в подынтегральном выражении просто не существует.3 Поэтому пока не ясен смысл появляющегося

3 В теории интеграла Римана доказывается, что он может быть определен только для ограниченных функций. В то же время не существует никакой ограниченной обычной функции, которая могла бы удовлетворить основному условию, содержащемуся в определении 5.1.

85

∫−∞∞

интеграла, но несколько позже он будет объяснен ( опять же не вполне строго), причем данный ниже комментарий мог бы быть доведен до вполне строгих рассуждений в рамках соответствующего формализма.4 Так или иначе, будем надеяться, что данное здесь нестрогое определение дельтафункции в совокупности с последующим комментарием позволит прикладникам получить необходимое для практических целей представление об этом объекте на понятийном уровне.

Поскольку наши рассуждения не являются вполне строгими, мы позволим себе иногда проводить определенные формальные выкладки, не затрудняя себя соответствующими обоснованиями. В частности, элементарное преобразование подынтегрального выражения в (5.1), заключающееся в замене подынтегральной функции f(t) → f(t+t0) и последующей замене переменной интегрирования t → t-t0 приводит к более общей, чем (5.1), формуле

∞	δ(t−	t0	) f (t) dt =	f (	) ,	(5.2)
∫−∞				t0

при любом фиксированном t0 и для любой непрерывной функции f(t). Формулу (5.2) можно рассматривать, как одно из важнейших свойств дельта-функции. Еще одно важное свойство дельта-функции — ее четность

δ(t) = δ(-t), t (−∞;∞)

можно также формально получить из (5.1) заменой переменной t → -t в интеграле. Наконец, полагая, в частности, f(t) ≡ 1,

приходим к формуле

δ(t) dt =1 .

4 На самом деле такой комментарий представляет собой не что иное, как упрощенное объяснение так называемого секвенциального подхода к

определению обобщенных функций (см.,		например, книгу	П. Антосик,
Я. Микусинский, Р. Сикорский,	Теория	обобщенных	функций.
Секвенциальный подход, М.: Мир,	1976).

86

На это свойство часто ссылаются, как на свойство нормировки дельта-функции.

В русле комментария введенных выше понятий проведем далее некоторые рассуждения, в которых появляющиеся интегралы будут пониматься в смысле обычного интеграла Римана.

Заметим, прежде всего, что для любой непрерывной

	функции f(t) имеет место формула
	f (0) = lim			1		∫ ε		f (t) dt .	(5.3)
				2ε			ε
		ε→0				−
	Действительно, по теореме о среднем значении для любого
	ε > 0 существует τ (−ε;ε), такое, что
		∫−εε f (t) dt = 2ε f (τ) ,
	и, следовательно,
		1	∫ ε		f (t) dt = f (τ) .
		2ε		−ε

Очевидно, что при ε →0 будем иметь τ → 0, так что при

стремлении ε к нулю правая часть последнего равенства будет стремиться к f(0), и, таким образом, после предельного перехода ε →0 в обеих частях этого равенства получается

формула (5.3).

Вводя теперь функцию

0,				t			>ε
δε (t)=	1	,		t			≤ε
	2ε

и учитывая, что эта функция обращается в нуль за пределами отрезка [−ε ;ε], вычислим интеграл5:

5 Функция δε (t) f (t) не является непрерывной, но является ограниченной

при любом фиксированном ε > 0 и имеет конечное число разрывов (более точно, два разрыва), а потому существует интеграл Римана от этой функции.

87

∫ ∞	δ	(t) f (t) dt = ∫ ε	1	f (t) dt=	1	∫ ε		f (t) dt .
					2ε
−∞	ε	−ε 2ε				−	ε

Сравнивая полученную формулу с предельным соотношением (5.3), приходим к выводу, что

limε→0 ∫−∞∞δε (t) f (t) dt = f (0) ,

или с учетом определения 5.1

limε→0 ∫−∞∞ δε (t)f (t)dt = ∫−∞∞ δ(t)f (t)dt,

где интеграл в левой части равенства – обычный интеграл Римана, а интеграл в правой части содержит дельта-функцию и понимается, как было отмечено выше, в более общем смысле. Есть возможность прояснить этот смысл. А именно интеграл в указанном более общем смысле от произведения дельтафункции на непрерывную функцию f(t) может пониматься как предел при ε →0 обычного интеграла Римана, содержащего в

подынтегральной функции произведение функции δε (t) на все

ту же функцию f(t). С другой стороны, проведенные рассуждения показывают, что саму дельта-функцию δ(t) можно рассматривать как результат перехода к пределу в некотором смысле при ε →0 последовательности функций δε (t), но сам

переход к пределу использует конструкцию интеграла Римана и не эквивалентен обычному (поточечному) переходу к пределу последовательности функций при каждом фиксированном t (− ∞;∞). Саму последовательность δε (t) часто называют

дельта-образной последовательностью.

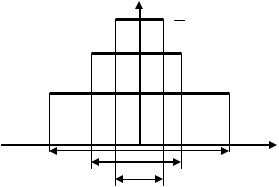
Рассмотрим попутно,			к	чему приводит поточечный
переход к	пределу	при ε →0		последовательности функций
δε (t). На	рис.5.1	изображены		графики этих функций при

различных ε . Из этого рисунка непосредственно видно, что
при ε →0	носитель функцииδε (t) стягивается к началу
координат и,	следовательно, при любом фиксированном t ≠ 0

будет выполняться limδε (t) = 0 .

ε→∞

88

у

1

2ε

х

2 ε

Рис. 5.1. Поточечная сходимость дельта-образной последовательности

С другой стороны, поскольку максимальное значение функции δε (t) неограниченно возрастает при ε →0 , ясно, что тогда

должно выполняться δε (0)→ ∞ . Итак, понимая переход к пределу в смысле поточечной сходимости, получаем

	0,	t ≠ 0	.
limδε (t) =
ε →0	∞, t = 0

Если считать, что поточечный переход к пределу также должен приводить к дельта-функции, можно было бы тогда написать формулу

δ(t)= 0, t ≠ 0 .	(5.4)
∞, t = 0

И, действительно, в некоторых учебниках включают последнюю формулу в определение дельта-функции, пытаясь затем использовать ее в русле обычного математического анализа и игнорируя тот факт, что в стандартном математическом анализе не используются функции, обращающиеся в бесконечность, так как в рамках этой

89

дисциплины не развиты средства для работы с такими функциями.

В то же время в теории обобщенных функций доказывается, что дельта-функции δ(t) можно приписать поточечные значения во всех точках кроме t = 0, а именно δ(t) = 0 при t ≠ 0. Данный факт говорит о том, что формула (5.4) имеет смысл по крайней мере частично.

5.2 Случайные процессы

Введем теперь некоторые базовые определения из теории случайных процессов, которые потребуются нам при обсуждении центральных вопросов данной главы.

Определение 5.2. Будем говорить, что на числовом множестве T задана случайная функция X = X(t), если каждому t из множества T однозначно поставлена в соответствие по некоторому закону случайная величина X. Если аргумент t играет роль времени, то вместо термина

“случайная функция” используют термин “случайный процесс”.

Таким образом, случайная функция (случайный процесс) – это функция, значениями которой являются случайные величины.

При изучении случайных процессов – а именно они будут объектом нашего внимания – будем считать, что случайный процесс X(t) определен при t ≥ t0 , где t0 – некоторое заданное

число. Наиболее часто будет встречаться ситуация, когда случайный процесс определен при t ≥ 0.

Определение 5.3. Каждое испытание (эксперимент), связанное (связанный) со случайным процессом X(t), в своем исходе дает некоторую числовую функцию x(t), которая

90