Бакаев Методы статистических испытаний 2007

отвергнуть гипотезу, называют критерием Пирсона или

критерием согласия χ2.

Как будет видно позднее, в принципе достаточно для любой практической задачи иметь в распоряжении совокупность случайных чисел, распределенных равномерно на интервале (0; 1). Поэтому будем применять критерий χ2 для проверки равномерного закона распределения.

Фиксируем достаточно близкую к 1 вероятность β, которую будем называть доверительной вероятностью или

коэффициентом доверия. Противоположную вероятность 1−β часто называют уровнем значимости. Теоретически в качестве доверительной вероятности можно принять любое число β (0;1). С практической же точки зрения тот или иной выбор β означает, что для данной практической задачи принимается договоренность, согласно которой при единичном испытании любое событие с вероятностью, не меньшей β, считается практически достоверным, а событие с вероятностью, не большей 1−β, считается практически невозможным.23

Предположим теперь, что имеется некоторая одномерная непрерывная случайная величина X, принимающая значения из интервала (0; 1).24 Выдвинем гипотезу о том, что X равномерно распределена на (0; 1). Предположим, что имеется N независимых экспериментальных значений (N достаточно велико) x1, x2, …, xN этой случайной величины. Обсудим вопрос, как можно воспользоваться этими значениями для проверки выдвинутой гипотезы.

23 Подобные рассуждения имеют чисто интуитивный характер, но они вполне устраивают многих практических пользователей, не желающих вдаваться в более строгие рассуждения, касающиеся проверки статистических гипотез. Желающие получить более глубокие представления о развитой теории проверки статистических гипотез могут ознакомиться с книгами Г. Крамера [13] и В.Е. Гмурмана [8].

24 Как уже упоминалось, можно считать, что X принимает значения из отрезка [0;1], поскольку X принимает краевые значения 0 и 1 с нулевыми вероятностями.

41

Выберем некоторое натуральное число r и представим интервал (0; 1) в виде r попарно непересекающихся числовых промежутков ∆j ненулевой длины, из которых первые r −1 являются открытыми слева полуинтервалами, а последний (r-й)

– интервалом, так что

(0;1)= ∆ ∆ ... ∆r , ∆i ∩ ∆j = 0 , i ≠ j .

Обозначая через pj длину промежутка ∆j, будем тогда очевидно иметь

	p + p	+ ... + pr = .
Нетрудно	также видеть,	что pj = P({X ∆j }),		j = 1, 2,…, r.
Теперь по экспериментальным			значениям	x1, x2,…, xN
вычислим	ν1, ν2,…, νr (этот этап		называется в	статистике

группировкой значений),25 а далее по формуле (3.6) – величину

χN Если наша гипотеза справедлива, то случайная величина

χN , числовая реализация которой вычислена по формуле (3.6),

должна при достаточно большом N хорошо подчиняться закону распределения χ2 с (r −1)-й степенью свободы. Определим теперь из уравнения

∞∫ kr −1 (x) d x =1− β

χ2 (r −1,1−β)

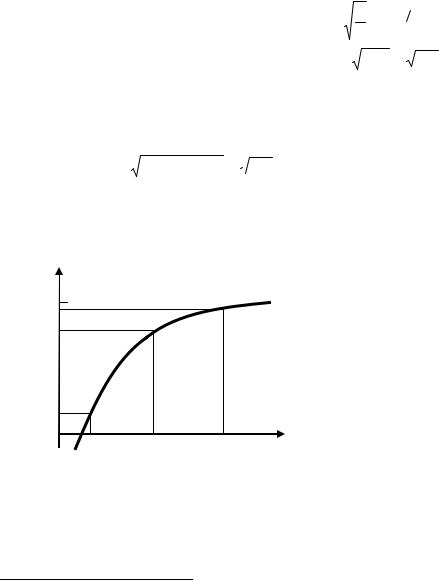
числовое значение величины χ2(r−1, 1−β), отвечающее принятому нами уровню значимости 1−β (рис 3.5). Для практического решения этого уравнения разработаны таблицы (см. Приложение 1).

25 Напомним, что в связи с принятой ранее системой обозначений символом νj обозначается количество выборочных значений данной случайной величины, попадающих в ∆j.

42

y

x

y = ∫ k m (x )d x

0

0	χ2(m, 1-β)	х

Рис. 3.5: Вычисление χ2(m,1-β)

Если для вычисленного по формуле (3.6) значения χN выполняется

χN2 < χ2 (r−1,1− β),

(3.7)

то на практике гипотеза принимается,26 а в случае противоположного неравенства гипотеза отбрасывается.

Ясно, что итоговый результат проверки зависит от выбранной доверительной вероятности. Наиболее часто на практике используют значения доверительной вероятности β = 0,95; 0,99; 0,999 – соответствующие уровни значимости

1−β = 0,05; 0,01; 0,001 называют 5 %-, 1 %-, и 0,1 %-ными уровнями. Если противоположное к (3.7) неравенство

выполняется при β = 0,95, то соответствующее значение χ2N

называется почти значимым, при β = 0,99 – значимым, а при β = 0,999 – высоко значимым (рис 3.6).

Как уже было сказано, на практике широко распространено использование таблиц значений величины χ2(m,1−β), являющейся корнем уравнения

∞∫ km (x) d x =1− β.

χ2 (m,1−β)

26 На самом деле неравенство (3.7) означает всего лишь, что подсчитанное числовое значение χ2N не противоречит выдвинутой гипотезе (см. по этому поводу, например, книги [8,13].)

43

Однако в таких таблицах число степеней свободы m обычно не превосходит 30. При больших значениях m можно использовать

таблицу значений интеграла вероятностей Φ(x)=	2	∫ x e−t 2 2	t ,
	π	0
так как в этом случае случайная величина Ζ =	2 χ2 −		2m

имеет распределение, близкое к нормальному с параметрами

(0,1).27 Поэтому при больших m

∫χ∞2 (m,` −β)km (x)d x ≈ 12 (1−Ф(z)),

z = 2 χ2 (m,1− β)− 2m.

Заметим, что к последней приближенной формуле существуют таблицы поправок.

у	y=∫x0km(x) dx

1.0

0.999

0.99

	почти	значимые	высоко
	значимые	значения	значимые значения
0.95	значения

х

χ2(m,5%) χ2(m,1%) χ2(m,0.1%)

Рис. 3.6. Уровни значимости

27 Имеется в виду нормальное распределение с математическим ожиданием и дисперсией, равными соответственно 0 и 1.

44

Пример 3.2. Предположим, что при r = 15 по имеющейся выборке получено значение χ2N =10.7. Примем в качестве

уровня значимости 1−β = 0,1. Тогда, полагая m = r −1 = 14, по таблице значений χ2(m,1 − β) находим χ2(m,1 − β) = 21.1. Таким

образом, поскольку χ2N < χ2(m, 1 − β), приходим к выводу, что

полученное значение χ2N допустимо для принятого	уровня
значимости.
Замечание 3.2. При фиксированном заранее значении N
нельзя бесконтрольно увеличивать r, так как величины	N pj

могут стать весьма малыми, а значения νj будут достаточно чувствительными к их вариациям (это явление называют неустойчивостью). Обычно рекомендуется выбирать ∆j таким образом, чтобы значения N pj не опускались ниже 20.

Критерий согласия ω2

Рассмотрим одномерную случайную величину X с функцией распределения F(x). Пусть далее x1, x2,…, xN – выборка из N независимых реализаций этой случайной величины. Построим эмпирическую или выборочную функцию распределения

FN (x)= N SN (x),

где SN(x) – количество выборочных значений, меньших x. Интуитивно понятно, что выборочная функция распределения

FN (x) должна быть близка к точной функции распределения F(x) при достаточно больших N. Точный смысл такой близости указывается в теории вероятностей. А именно, так как FN (x) –

это частота появления события {X < x} в N независимых испытаниях, F(x) представляет собой вероятность этого

45

события, то есть P ({X < x}) = F(x) то, как следует из теории вероятностей (см., например, книги [8,13]), FN (x) сходится по вероятности к F(x) при N → ∞. Последнее означает, что при любых фиксированных x (− ∞;∞) и ε > 0 имеет место предельное соотношение

lim P({FN (x)− F(x) ≥ ε})= 0 .

N→∞

В качестве меры расхождения между FN (x) и F(x) часто используют величину28

∞

ωN2 = N ∫ (FN (x)− F (x)) 2 d F (x). (3.8)

−∞

Теорема 3.3. (Р. Мизес, Н. В. Смирнов)

Какова бы ни была одномерная случайная величина X с непрерывной функцией распределения F(x), при произвольном фиксированном x>0 имеет место предельная формула

Nlim→∞ P( { ωN2 < x } )= a1 (x),

где функция a1(x) не зависит от X.

Приведенная теорема положена в основу так называемого критерия согласия ω2. Этот критерий позволяет проверять гипотезы о функции распределения одномерной непрерывной случайной величины X.

Схема применения этого критерия буквально дублирует описанную ранее схему в случае критерия χ2. А именно,

28 Присутствие фактора dF(x) означает, что интеграл понимается в смысле Лебега-Стильтьеса (см., например, книгу Г. Крамера [13]. Для читателей, незнакомых с этим математическим аппаратом, укажем, что для гладких функций F(x) можно считать dF(x) = F′(x) dx и понимать указанный интеграл в обычном смысле Римана.

46

критерий ω2 применяется следующим образом.29 Прежде всего фиксируется доверительная вероятность β и из уравнения

a1(ω2 (β))= β

определяется критическое значение ω2(β). Для решения этого уравнения можно воспользоваться таблицей функции a1(x) (см. Приложение 2). Далее, по формуле (3.8) вычисляется

величина ωN2 и выполняется проверка неравенства

ωN2 < ω2 (β).

Если последнее неравенство выполняется, то вычисленное значение ωN2 3допустимо, то есть оно не противоречит гипотезе о том, что искомая случайная величина имеет функцию распределения F(x). В случае же нарушения указанного неравенства делается вывод о том, что практическое значение ωN2 противоречит данной гипотезе (при выбранном уровне значимости).

По сравнению с критерием χ2 критерий ω2 имеет то очевидное и важное преимущество, что не нужна группировка выборочных значений (и, следовательно, отпадает необходимость во введении дополнительного параметра r). Заметим, что на практике критерий ω2 применяют уже при

N ≥ 50. Однако для практического вычисления ωN2 требуется предварительно расположить выборочные значения x1, x2, …, xN в порядке возрастания

x{1} ,x{2} ,...,x{N} .

Такая упорядоченная выборка называется в статистике

вариационным рядом, его члены называются порядковыми статистиками. Необходимость упорядочения исходной выборки при больших N может привести к существенному

29 Для успешного применения этого критерия N должно быть достаточно велико.

47

увеличению трудоемкости алгоритма, реализующего критерий

ω2.

Обсудим теперь применение критерия ω2 в специальном интересующем нас случае, когда выдвигается гипотеза о равномерном законе распределения. Следовательно, необходимо положить F(x) = x при x (0; 1).30 Выведем теперь

полезную формулу для ωN2 . Нетрудно видеть, что

F (x)=	k	при x{k} < x ≤ x{k + }, k = 0,1,...,N .
N	N

Далее для удобства наших дальнейших рассуждений положим x{0} = 0 и x{N+1} = 1.31 Тогда имеет место цепочка равенств

ωN2

N x{k +1}

k

2

=

∑

∫

F(x)−

dF

(x)=

N

N

k =0 x{k }

N x{k +1}

k 2

=

∑

∫

x −

dx =

N

k =0 x{k }

N x3

2 k x2

k 2 x

x

= x{k +1}

= ∑

−

+

=

2

3

N 2

N

x

= x{k}

k =0

N

k

k

2

1

3

3

2

2

= ∑

(x{k +1} − x{k})−

(x{k +1} − x{k})+

(x{k +1} − x{k})

=

N

N

2

k =0

3

N

x{3k +1}

kx{2k +1}

k 2 x{k +1}

=

∑

−

+

−

3

N

N

2

k =0

N

x{3k}

(k −1)x{2k}

(k −1)2 x{k}

−

∑

−

+

+

2

3

N

N

k =0

N

1

2

2 k −

1

+

∑

x{k}−

N

x{k}

.

k =0

N

30Очевидно также, что F(x) = 0 при x ≤ 0 и F(x) = 1 при x ≥ 1.

31Напомним, что речь идет о проверке равномерного закона распределения и потому любые выборочные значения должны

принадлежать интервалу (0;1). Таким образом, x{0} и x{N+1} являются экстремальными значениями для любой выборки.

48

Заметим, что комбинация первых двух слагаемых в самой правой части этого равенства легко вычисляется за счет взаимного уничтожения почти всех членов в соответствующих суммах. После дополнения до полного квадрата выражения, стоящего под знаком суммы в третьем слагаемом, получим

1

2

1

2

2

1

N

k−

k−

2

2

ωN

= 1

+

∑

x{2k}−

2k−1 x{k}+

−

.

N

N

N

3

N k =0

N

1

2

N

k−

N

1

2

Поскольку

величина

∑

=

−

легко

N

3

12 N

k=0

вычисляется, приходим окончательно к формуле

k−

1

2

1

N

2

ωN2 =

+ ∑

x{k}

−

,

12 N

N

k =1

которая и является основой при применении критерия ω2 для проверки гипотезы о равномерном законе распределения.

Проверка таблиц случайных цифр

Остановимся теперь на некоторых деталях проверки таблиц случайных цифр ε1,ε2,…,εN 32.

Для проверки таблиц М.Г. Кендалл и Б.Б. Смит предложили использовать четыре теста. В каждом из них цифры классифицируется по некоторому признаку и эмпирические частоты сравниваются с их математическими

32 Таблицы случайных цифр хороши тем, что из их элементов можно “нарезать” случайные числа с любым желаемым числом десятичных знаков.

49

ожиданиями при помощи критерия χ2. Согласно упомянутым авторам в качестве тестов берутся:

•проверка частот (frequency test). Проверяется частота появления различных цифр в таблице;

•проверка пар (serial test). Проверяется частота

появления различных двузначных чисел среди пар

ε1ε2 ,ε2 ε3 ,…,ε N −1ε N ;

•проверка интервалов (gap test). Проверяется частота появления различных интервалов между двумя последовательными нулями;

•проверка комбинаций (poker test). Проверяется частота различных типов четверок (abcd, aabc, aaab, aaaa) среди

четверок ε1ε2 ε3ε4 ,ε2 ε3ε4 ε5 ,…,ε N −3ε N −2 ε N −1ε N .

Большинство последующих авторов также использовали указанную систему тестов, вводя, однако, в нее некоторые модификации, среди которых отметим лишь две. Вместо проверки интервалов часто предлагалось использовать проверку серий (run test): считается, что цифры εk +1,εk +2,…,εk +l

образуют	серию длины	l, если εk +1 =εk +2 =…= εk +l , но
εk ≠ εk +1 и	εk +l +1 ≠ εk +l .	Кроме того, предлагалось вместо

проверки пар ε1ε2 ,ε2 ε3 ,ε3ε4…проверять независимые пары...

ε1ε2 ,ε3ε4 ,ε5 ε6….

Безусловно, самые важные тесты – проверка частот и проверка независимых пар. Проверка серий также выдвигает определенные требования “случайности”. В то же время считается, что проверка комбинаций носит несколько искусственный характер. Например, И. М. Соболь рекомендует в качестве основных следующие два теста:

Первый тест (проверка частот и пар). Предполагается,

что количество цифр в таблице – четное, то есть N = 2N′. Далее цифры ε1 ,ε2 ,…,εN разбиваются на пары ε1ε2 ,ε2 ε3 ,…,ε N −1ε N . Обозначим через νij наблюдаемое количество пар i j. Используя вычисленные значения νij, 0 ≤ i, j ≤ 9, можно также определить величины

50