Бакаев Методы статистических испытаний 2007

Для упрощения методики моделирования перейдем к сферическим координатам r,ϑ, ϕ , которые связаны с

декартовыми посредством формул

x = r sinϑcosϕ,		y = r sinϑsinϕ,		z = r cosϑ,
0 ≤ r <1, 0 ≤ϑ < π,			0 ≤ϕ < 2π.
Если в	указанные		формулы	вместо	x, y, z, r, ϑ иϕ
подставить соответственно X, Y, Z, R,				Θ и Φ,	то получается
фактически связь между старыми (декартовыми)						случайными
величинами	X, Y, Z	и новыми (сферическими)				случайными

величинами R, Θ , Φ, принимающими свои значения в интервалах (0; 1), (0; π) и (0; 2π), соответственно. Поскольку якобиан преобразования от декартовых координат к сферическим известен

∂(x, y,z) = r 2 sinϑ ,

∂(r,ϑ,ϕ)

то легко выписать плотность распределения в новых координатах (обозначим ее через q(r,ϑ,ϕ)):

	q(r,ϑ,ϕ)= p(x, y,z)	∂(x, y,z)		=	3	r 2 sinϑ .
		∂(r,ϑ,ϕ)			4π

Как нетрудно заметить, последняя формула может быть переписана в виде

q(r,ϑ,ϕ) = (3r 2) (12 sinϑ)(2π)-1 .

Поскольку каждый из множителей, выделенных структурно в правой части, представляет собой плотность одномерного распределения случайной величины R, Θ и Φ, соответственно, то совместная плотность распределения трехмерной случайной величины (R, Θ ,Φ) представляется в виде произведения соответствующих одномерных плоскостей, что в свою очередь

71

свидетельствует о взаимной независимости одномерных случайных величин R, Θ иΦ. Таким образом, эти случайные величины можно моделировать независимо друг от друга, используя формулы метода обратных функций,

∫R 3r 2 d r = Γ		,	1	∫Θsinϑ dϑ = Γ		,	1	∫Φ	dϕ = Γ		,
			2				2 π
0	1			0	2			0		3

что впрочем, эквивалентно более простым формулам

R = 3 Γ ,	cosΘ =1− 2 Γ	2	,	Φ = 2πΓ	3	.
1

Окончательно, используя результаты моделирования для R, Θ , Φ можно вернуться к исходным случайным величинам по формулам

X = Rsin ΘсоsΦ , Y = Rsin ΘsinΦ, Z = R cosΘ .

Моделирование многомерной нормальной случайной величины с коррелированными координатами

Корреляция является одной из самых больших проблем, с которыми сталкиваются количественные аналитики и рискменеджеры, практикующие методы статистического моделирования для принятия финансово-инвестиционных решений. В частности, самооценка подверженности риску любого инвестиционного банка, часто рассчитываемая как квантиль VaR (Value at Risk), также заметно меняется при варьировании предположений о взаимозависимости между всеми вовлеченными рыночными факторами риска.

Остановимся подробно на исследовании наиболее важного для практики частного случая, когда моделируется многомерная нормально распределенная случайная величина с заданной матрицей ковариации С и с нулевыми

72

математическими ожиданиями.7 Итак, будем моделировать многомерную случайную величину Х = (Х1; Х2; …; Хn) с (совместной) плотностью распределения

p(x) = p(x1, x2 ,…, xn) = (2π)−

n

1

e−

1

C

−1

x,x ,

2

C

−

2

2

где |С| – определитель матрицы

С,

x,y = ∑in=1 xi yi

–

скалярное

произведение

векторов

x = (x1; x2;…; xn)

и

y = (y1; y2;…;yn), а

C −1 x ,x

– соответственно

квадратичная

форма, порожденная матрицей С -1, то есть

n

n

n

−1 ) xi x j .

C−1 x,x = ∑(C−1 x ) xi = ∑ ∑(C

i=1

i

i=1 j=1

ij

Нам

будет

удобно

ввести

набор

новых

координат

y = (y1 ; y2;…;yn),

связанных

со

старыми

посредством

матричного преобразования
x=Vy,	(4.9)
где V = (vij) – некоторая (пока не определенная)	n × n – мат-

рица. Тогда квадратичную форму <C -1x,x> можно расписать в новых координатах как

<C -1x,x> = <C -1Vy, Vy>,

или, используя известные свойства матричных операций,

<C -1x,x> = <V TC -1Vy,y>,

(4.10)

где VT — матрица, транспонированная к матрице V. Потребуем теперь, чтобы8

7Впрочем, приведенная ниже техника легко обобщается на случай ненулевых математических ожиданий.

8 Напомним, что конкретный вид матриц V до сих пор не был еще определен.

73

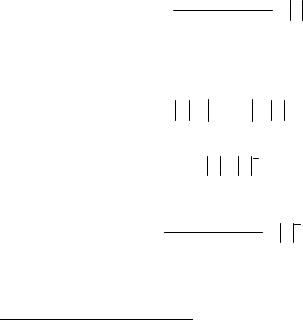
V TC -1V = E,

(4.11)

где Е — единичная матрица порядка n. Умножая последнее матричное соотношение слева на (VT)-1, а справа на V -1, приходим к формуле

C -1=(V T) -1V -1,
откуда для самой матрицы С получаем9
С=VV T.	(4.12)

Считая в дальнейшем, что матрица V подобрана в соответствии с условием (4.12), якобиан преобразования (4.9) легко вычисляется10 и равен:

∂(x1; x2 ;…;xn ) = V . ∂( y1; y2 ;…; yn )

Кроме того, используя формулу (4.12), имеем, применяя известные свойства определителей,

C = V VT = V 2 ,

откуда

1

V = C 2 ,

так что на самом деле можно получить

∂(x1; x2 ;…; xn ) = С 1 .

2

∂( y1; y2 ;…; yn )

Последний результат позволяет с учетом (4.10) и (4.11) вычислить плотность распределения в новых координатах

9Напомним, что, как известно из теории матриц (см., например, [ 6, п. 4.59]), при обращении матричного произведения порядок матричных сомножителей изменяется на противоположный.

10Заметим, что это преобразование — линейное.

74

q( y , y

,…, y

n

) =

p(x ,x

,…,x

n

)

∂(x1; x2 ;…; xn )

=

1

2

1

2

∂( y ; y

2

;…; y

n

)

1

n

1

−

1

C −1х,х

1

−

C

−

2

e

C

2

=

2

2

= (2 π)

1

1

= (2 π)−n2

e−

C −1х,х = (2 π)−n2 e−

у,у =

2

2

n

−

1

−

yi2

= ∏

2 e

2

,

(2 π)

откуда

следует,

i

=1

в

плотность

что

новых координатах

распределения представляется как произведение одномерных плотностей, каждая из которых соответствует нормальному распределению с параметрами (0,1). Обозначая набор соответствующих одномерных случайных величин через Y = (Y1;Y2;…;Yn), можно сделать вывод, что имеет место связь

X = V Y,

(4.13)

а, кроме того, все Y1,Y2,…,Yn – независимы и каждая из них распределена по нормальному закону с параметрами (0,1). Вопрос моделирования таких случайных величин уже обсуждался в параграфе 4.1. Окончательное моделирование многомерной случайной величины Х проводится на основе применения матричного соотношения (4.13).

Остался невыясненным вопрос нахождения матрицы V, удовлетворяющей соотношению (4.12). Известно, что матрица ковариации С симметрична и положительно определена. Из теории матриц следует11, что в этом случае существует нижняя треугольная матрица V, удовлетворяющая условию (4.12). Это соображение значительно облегчает построение нужной матрицы V, так как достаточно искать ее в классе нижних треугольных матриц. Другими словами, для матрицы V = (vij )n×n можно считать, что vij = 0 при i < j , а

11 См., например, [6, п. 11.10]

75

элементы vij с i ≥ j (их общее количество равно n (n+1)/2) определяются тогда из n (n+1)/2 уравнений

∑j vilvjl = cij ,	1 ≤ j ≤ i ≤ n,
l =1

где cij – элементы матрицы С. Удобно решать последнюю систему, например, по схеме, указанной на рис. 4.2.

Рис. 4.2. Схема последовательного определения элементов матрицы V

Пример 4.5. Пусть требуется смоделировать нормально распределенные случайные величины Х1 и Х2 с параметрами (0,1) и с заданным коэффициентом корреляции ρ = M[X1 X 2 ].12

В качестве исходных объектов для моделирования примем независимые случайные величины Y1 и Y2, каждая из которых распределена нормально с параметрами (0,1). Как уже неоднократно отмечалось ранее, их моделирование представляет собой стандартную и хорошо изученную задачу. Матрица ковариации для моделируемых случайных величин X1 и X2 имеет вид

1		ρ
С =			.
	ρ	1

12Напомним, что коэффициент корреляции всегда удовлетворяет условию

ρ[−1;1].

76

Легко тогда проверить, что матрица

1

0

2

V =

ρ

1−

ρ

удовлетворяет условию

1

0 1

ρ

1

ρ

= C .

VV T =

2

2

=

−

ρ

0

1−

ρ

ρ 1

ρ

1

Таким образом, X1 и X2

могут быть смоделированы на основе

формулы (4.13) путем использования соотношений:

X1=Y1, X 2 = ρY1 + 1− ρ2 Y2 .

4.4 Метод суперпозиции

Предположим, что функция F(x) одномерной случайной величины X представима в виде

m	(4.14)
F(x) = ∑ck Fk (x) ,
k=1
где Fk (x ) – некоторые функции распределения,	а все

коэффициенты разложения ck > 0, k = 1,2,…,m. В частности, допустимо принять m = ∞ . Полагая в обеих частях данного равенства х → ∞ и пользуясь известным свойством функций распределения

lim F(x)=lim Fk (x)=1,

x→∞ x→∞

приходим к выводу, что с необходимостью должно выполняться

77

m

∑ck =c1 + c2 +…+ cm =1.

k =1

Таким образом, коэффициенты сk, k = 1, 2,…, m, имеют смысл вероятностей, с которыми некоторая дискретная случайная величина принимает свои значения. Основываясь на этом наблюдении, введем дискретную случайную величину Y с законом распределения

	1	2		…		m
	c1	c2		…		cm
так что P ({Y = k })= ck ,		k=1,2,…,m.
Метод суперпозиции был предложен Дж. Батлером13 и
состоит фактически в следующем.
Пусть Г1 и Г2 — независимые случайные числа. Пусть
вначале число Г1 используется для					моделирования значения
Y = k случайной величины Y14, а затем						при соответствующем

k случайная величина Х моделируется путем решения уравнения Fk(x) = Г2, тогда смоделированная таким образом

случайная величина	Х	будет	иметь как раз функцию
распределения F(х).
Действительно,	достаточно		применить формулу полной
вероятности
P({X < x })= ∑ P		({ X < x |Y = k })= ∑Fk (x)ck = F(x)		,
m			m
k =1			k =1

откуда и следует, что F(х) – функция распределения случайной величины Х.

13См. J. W. Butler, Machine sampling from given probability distributions, Symposium on Monte Carlo methods, ed. H.A. Meyer, Wiley, New York, 1956, p. 249-264.

14См. параграф 4.1.

78

m	Fk (x) возникают
Функции распределения вида F(x)= ∑ ck
k=1

на практике, когда появляется смесь из случайных величин, различным образом распределенных. В этом случае применение метода суперпозиции является по существу рецептом для моделирования случайной величины Х с функцией распределения F(x).

С другой стороны, представление (4.14) зачастую вводится искусственным образом с целью облегчить процедуру моделирования искомой случайной величины X. Следующий пример демонстрирует один из часто применяемых приемов моделирования, использующих идею метода суперпозиции.

Пример 4.6 (Дж. Батлер)

Пусть случайная величина X принимает значения в интервале (0;1) и пусть ее функция распределения представима рядом

∞	(4.15)
F(x) = ∑ck xk ,

k =1

∞

где ck ≥ 0 при всех k=1,2,… и ∑ck =1. Требуется построить

k =1

рациональный алгоритм моделирования случайной величины X.

Прежде всего заметим, что представление (4.15) есть по существу разложение функции распределения в ряд Маклорена, при этом вытекающее из (4.15) условие F(0) = 0 является естественным, так как значения Х сосредоточены на интервале

(0;1).

Далее, положим Fk(x) := xk при x (0;1)15 и воспользуемся для моделирования принципом суперпозиции, который в

15 Очевидно, Fk(x) удовлетворяет всем свойствам функции распределения.

79

данном конкретном случае реализуется по двухступенчатой схеме16:

а) сначала из условия

k −1	k
∑c j < Г1	≤∑c j
j=1	j=1

выбирается k;

б) затем моделируется сама случайная величина Х по формуле

1

X = (Г2)k .

Пример 4.7. Рассмотрим для иллюстрации более конкретную версию предыдущего примера. Пусть случайная величина Х принимает значение в интервале (0; 1) и пусть ее плотность распределения представима в виде

p(x)= c(2 x+6 x5 ) .

Требуется смоделировать случайную величину Х.

Определим вначале численное значение константы c из условия нормировки

						1 = ∫01 ρ(x) d x = c ∫01(2 x+ 6 x5 ) d x = 2c ,
то есть			c =		1	. При этом для функции распределения имеем
(	)		2	2
F x		=	1	(x 2		+ x 6 ) . Далее, полагая F1(x) = x2 и F2(x) = x6,

представим F(x) как

F(x) = c1F1(x)+c2F2(x).

16 Как и выше, через Г1 и Г2 обозначается пара независимых случайных чисел.

80