Бакаев Методы статистических испытаний 2007

причем Е1 Е2… Еk-1 могут принимать любые цифровые значения (от 0 до 9). Длина интервала, на котором выполняется это двойное неравенство, в точности равна 10-k. Поскольку при различных значениях i такие интервалы не пересекаются, то, как показывает простейшее вычисление,

P({ = i})= ∑10−k = k −1				−k = 1 .
Ek	9	10 10
	E1E2 ,…,Ek −1=0			10
Покажем, что Еs и Еk независимы при s			≠ k. Будем считать
для определенности, что 1 ≤ s < k.		Вычислим вероятность

одновременного наступления событий {Ek = i} и {Es = j}. Очевидно, оба события наступают одновременно тогда и только тогда, когда выполнено неравенство (3.1) и в то же время выполняется {Es = j}. Поэтому2

P({ = i} { = j}) =		∑10−k	= 1 .
Ek	Es	9
		E1E2 ,…,Es−1,Es+1,…,Ek −1=0	100

В русле аналогичных соображений нетрудно также показать, что

P ({Еk1 = i1} {Еk 2 = i 2} … {Еk s = i s})= 10 − s ,

и, таким образом,

P ( {Еk1 = i1 } {Еk2 = i2 } … {Еks = is }) =

= P ({Еk1 = i1}) P ({Еk 2 = i 2}) P ({Еk s = i s}).

Как следует из теоремы умножения теории вероятностей, последнее равенство свидетельствует о независимости

2 Здесь и далее используем символ конъюнкции , который является синонимом логического «и».

21

случайных цифр Еk1 ,Еk2 ,…,Еks при любых наборах попарно

различных натуральных чисел k1 k2,…,ks.

Обратимся теперь к доказательству второй части утверждения теоремы, которое фактически является обратным утверждением к уже доказанному. Пусть теперь E1, E2,…, Ek,…

– независимые случайные цифры. Произвольное фиксированное число γ (0; 1) может быть представлено в виде бесконечной десятичной дроби

γ = 0.e1e2…ek… .

Неравенство Γ < γ очевидно означает, что либо E1 < e1, либо

E1 = e1 и E2 < e2, либо E1 = e1, E2 = e2 и E3 < e3, и т.д.

Следовательно,

P ({Γ < γ }) =

∞

= ∑P({E1 = e1} {E2 = e2} ... {Ek −1 = ek −1} {Ek < ek }) ,

k=1

итак как все E1, E2, …,Ek, … независимы, то последнее соотношение может быть переписано в виде

P({Γ < γ}) =

∞

= ∑P({E1 = e1})P({E2 = e2 })...P({Ek −1 = ek−1})P({Ek < ek }) . (3.2)

k=1

	Далее	заметим,	1	что	P({E1 = e1}) = P({E2 = e2}) = …
	= P({Ek-1 = ek-1}) =			, в то	время как P({Ek < ek}) = ek10-1,
			10

посколькуEk может принимать значения 0, 1,…,ek −1 – каждое с

вероятностью	1	.	Подставляя	найденные	значения
10
вероятностей в формулу (3.2), окончательно получаем
			∞	∞
P ({Г < γ}) = ∑10−(k −1) ek 10−1 = ∑ek 10−k = γ ,
			k =1	k =1

22

что позволяет сделать вывод о равномерном распределении случайной величины Γ на интервале (0; 1).

Замечание 3.1. Так как в вычислениях всегда используются числа с конечным количеством десятичных знаков, то вместо случайных чисел Γ реально используют обрезанные случайные

числа Γ~ = 0 . E1E2 … En. При этом считается, что имеет место ошибка округления – как при любых приближенных вычислениях. В принципе, для конкретных алгоритмов МонтеКарло можно провести анализ влияния погрешности округления на результат вычисления – это делается по аналогии с оценкой влияния погрешности в курсе приближенных методов, и в дальнейшем мы оставляем такой анализ за бортом нашего основного исследования.

О некоторых других негативных последствиях операции округления случайных чисел можно прочитать в книге И. М. Соболя [18].

3.2 Способы генерации случайных чисел

Случайные числа неминуемо возникают в контексте любого метода Монте-Карло. Каковы же способы их получения? Оказывается, этот вопрос представляет собой отдельную важную проблему. Ниже обсуждаются три основных из практикуемых в различное время способа получения (генерации) случайных чисел. В дальнейшем будут указаны причины, по которым один из этих способов может считаться в настоящее время наиболее перспективным, поэтому он будет рассмотрен более подробно.

Таблицы случайных цифр

Если есть возможность каким-то способом получать независимые реализации случайной цифры E, то, записав эти реализации (в порядке их получения) в таблицу, получим так

23

называемую таблицу случайных цифр. Реализации случайного числа можно образовывать из элементов этой таблицы

Γ = 0.EsEs+1… Es+n-1

(с определенной ошибкой округления), где введение индекса s используется, чтобы показать, что выбор случайных цифр можно производить с любого места таблицы с номером s. При этом все последующие цифры можно выбирать как подряд, так и по любому алгоритму, не принимающему во внимание значения этих цифр.

Однако сами таблицы случайных цифр не выпадают на пользователя с неба в виде осадков – такие таблицы необходимо предварительно составлять каким-то способом. Отметим, что составление хорошей достаточно большой (>106 цифр) таблицы – крайне сложное дело. На настоящее время существуют разнообразные способы составления таблиц, но ни один из этих способов не гарантирует формирования абсолютно идеальной таблицы, элементы которой можно рассматривать как независимые реализации случайных цифр, по той простой причине, что на практике всегда в определенной степени нарушаются принципы равновероятности и независимости появления тех или иных цифр в таблице. Поэтому составленные таблицы проверяются некоторыми специальными способами на предмет удовлетворения таблицы указанным принципам.3 При этом проверяется частота появления отдельных цифр, частота появления различных соседних пар и т.п.

Может также возникнуть вопрос о законности многократного использования одной и той же таблицы. Обычно практических пользователей методов Монте-Карло этот вопрос не слишком беспокоит, так как даже интуитивно понятно, что

3 Вопрос о проверке таблиц случайных цифр будет более детально обсужден в дальнейшем.

24

таблицу можно повторно использовать при решении различных независимых задач. Впрочем такая возможность может быть даже строго доказана при определенных условиях теоретически.

Существует и другая опасность: если таблица очень большая, то ясно, что по законам случайности на отдельных ее участках возможно более частое повторение в определенных пределах какой-то цифры. В связи с этим не рекомендуется пользоваться наугад выбранными малыми участками очень большой таблицы. Таким образом, в идеале желательно под каждую задачу иметь заранее заготовленную таблицу подходящего размера.

Наконец заметим, что с возрастанием производительности современных компьютеров роль таблиц случайных цифр неуклонно снижается и, наоборот, все большую роль приобретают компьютерные методы генерации случайных чисел, которым в дальнейшем будет уделено особое внимание.

Датчики случайных чисел

В ходе развития практики применения методов МонтеКарло была также разработана возможность получения случайных чисел при помощи определенных технических устройств. Такие устройства получили название датчиков случайных чисел, в качестве которых часто использовали «шумящие» радиоэлектронные приборы.

Имея в распоряжении подобный прибор, можно для построения случайной последовательности использовать счетчик, который фиксирует количество флуктуаций (по mod 2) напряжения шумящего прибора, превышающих заданный уровень E0 за определенный заданный промежуток времени ∆t. Тогда за промежуток времени T = n ∆t с помощью такого технического устройства получается случайная последовательность из нулей и единиц длины n (рис.3.1).

Работа с датчиками создает проблемы, связанные с неидеальной случайностью получаемых чисел. Эти проблемы

25

здесь не обсуждаются, поскольку датчики случайных чисел в настоящее время практически вышли из употребления – опять же по причине того, что более перспективным является третий способ получения случайных чисел, описанный далее.

E

E0

∆t	∆t		t

Рис. 3.1. Иллюстрация действия датчика

Программы генерации псевдослучайных чисел

Наконец, третий способ получения случайных чисел – самый популярный в настоящее время – это способ, основанный на непосредственном использовании компьютеров, а более точно, на компьютерной реализации рекуррентной формулы

γn+1 = Ψ(γn), n=0, 1,2,…; γ0 задано.

(3.3)

Такие числа называются псевдослучайными.

Добавление приставки «псевдо», а ее использование в обыденной речи часто носит оттенок иронии, на самом деле не означает, что псевдослучайные числа в каком-то смысле хуже случайных чисел, получаемых другими способами. Как уже отмечалось выше, никакой способ получения случайных чисел не является абсолютно идеальным и элемент неслучайности всегда присутствует, какой бы механизм генерации ни был запущен. По-видимому, использование специальной терминологии в данном конкретном случае обусловлено тем, что само по себе применение какой-либо рекуррентной формулы является проявлением некоторой закономерности, что

26

должно было бы противоречить по своей природе принципу случайности. Не поддерживая в данный момент и не опровергая последний тезис, отложим более детальное обсуждение проблемы псевдослучайных чисел до следующего параграфа книги, специально посвященному этим числам ввиду их первостепенной важности для современных приложений. На данный момент лишь декларируется неидеальная случайность псевдослучайных чисел, обусловленная самим способом их получения. Однако этот способ выглядит настолько привлекательным, что были предприняты серьезнейшие попытки борьбы за качество псевдослучайных чисел, которые также обсуждаются ниже. Что касается очевидных достоинств метода псевдослучайных чисел, то к ним, в частности, относятся:

1)простота и быстрота их воспроизводства;

2)набор таких чисел достаточно один раз проверить, после чего их можно многократно использовать, восстанавливая по рекуррентной формуле.

Сдругой стороны, любая рекуррентная формула имеет свой предельный запас псевдослучайных чисел и это – недостаток данного метода.

Итак, выше обсуждены по крайней мере три способа получения случайных чисел. Еще раз подчеркнем то, что, как показала практика, по совокупности своих достоинств и недостатков наиболее привлекательным и потому наиболее употребительным является метод псевдослучайных чисел. Его детали излагаются в следующем параграфе.

27

3.3 Псевдослучайные числа

Любой, кто рассматривает арифметические методы создания случайных чисел, находится, конечно, в состоянии греха.

Дж. фон Нейман

Как было указано ранее, псевдослучайные числа получаются по рекуррентной формуле (3.3).

Это – рекуррентная формула первого порядка. В принципе возможно получение псевдослучайных чисел и на основе рекуррентных формул более высоких порядков, но такие формулы редко используются, поэтому дальнейшее

обсуждение будет посвящено написанной	выше	формуле
первого порядка.		Ψ(x) в
Весьма легко понять, что если функция
формуле (3.3) – гладкая, то соответствующая	последователь-

ность псевдослучайных чисел будет весьма «плохая». Действительно, если бы последовательность γ1, γ2,… была

действительно случайной,	то точки	с координатами
(γ1; γ2), (γ3; γ4), … были бы	хаотически	равномерно распре-

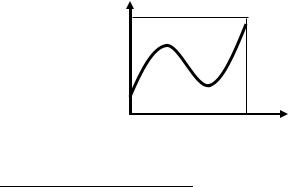
делены в единичном квадрате. Но все точки с координатами (γ1;Ψ(γ1)), (γ3;Ψ(γ3)), …, получаемые на основе генерации псевдослучайных чисел, лежат на графике функции y = Ψ(x).4

(рис.3.2).

1 у=Ψ(х)

			x
0		1

Рис. 3.2. Случай гладкой функции

4 Уместно вспомнить цитату Дж. фон Неймана, выбранную в качестве эпиграфа к данному параграфу.

28

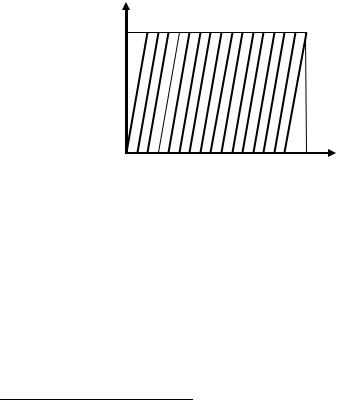
Поэтому для получения «хорошей» последовательности псевдослучайных чисел нужно, как минимум, использовать достаточно «плохую» функцию, точки графика которой достаточно плотно заняли бы единичный квадрат. Например, можно взять функцию y = {k x} при достаточно большом k > 0 (см. рис. 3.3).5

Функции именно такого вида действительно использовались в ряде алгоритмов генерации псевдослучайных чисел. Однако использование наугад выбранной плохой функции совсем не обязательно приводит к решению проблемы псевдослучайных чисел, что будет выяснено в ходе дальнейшего обсуждения.

у	у = {16х}
	1

0

1

х

Рис. 3.3. Случай негладкой функции

В связи с вышесказанным отметим, что какая бы плохая функция Ψ (x) не была выбрана, при компьютерной реализации формулы (3.3) всегда будут получаться периодические и, значит, неслучайные в конечном счете последовательности. Действительно, из-за конечной разрядности любого компьютера при его использовании всегда возможно записать лишь конечное (хотя, возможно, и очень большое) число различных чисел, заключенных между 0 и 1, и, таким образом, при каком-то (достаточно, может быть, большом) натуральном L значение γL совпадает с одним из предыдущих значений γl.

5 Операция {x} означает вычисление дробной части числа x.

29

Далее, очевидно, вычисление псевдослучайных чисел будет зацикливаться, так как ввиду формулы (3.3) будет выполняться равенство

γL+i = γl+i , i=0, 1,2,…

(3.4)

Определение 3.3. Пусть L – наименьшее натуральное число, при котором соотношение (3.4) удовлетворяется для некоторого l < L. Тогда множество чисел γ0, γ1,…, γL-1 называется отрезком апериодичности псевдослучайной последовательности (3.3), число L – длиной отрезка апериодичности, а Q = L – l – длиной периода этой последовательности.

Очевидно все числа, образующие отрезок апериодичности, различны. Кроме того, ясно, что для приложений нежелательно брать более чем L псевдослучайных чисел, генерируемых по формуле (3.3).

Однако даже если количество используемых псевдослучайных чисел меньше L, это еще не означает, что полученный набор псевдослучайных чисел не нуждается в проверке на случайность. А изобретение способов проверки на случайность также представляет собой отдельную важную (и сложную) проблему. И теоретики методов Монте-Карло разбились на два лагеря. Одни сосредоточились на изыскании способов улучшения случайности псевдослучайных чисел, в то время как другие пытались изобрести все более и более изощренные испытания на их случайность. Необходимо, однако, понимать, что каждый шаг непрерывной гонки в создании все более случайных чисел обречен на неудачу в некотором будущем, так как для любого нового метода, превосходящего на момент своего создания все существующие аналоги, рано или поздно будет построен тест, опровергающий случайность результатов, полученных по этому методу.

Таким образом, термин “псевдослучайные числа”

показывает, что ни при каком, даже самом изощренном способе

30