Бакаев Методы статистических испытаний 2007

их генерации такие числа могут считаться случайными лишь с определенными оговорками и в определенных пределах, но никогда они не будут являться идеально случайными.

Рассмотрим теперь некоторые конкретные подходы к генерации псевдослучайных чисел.

Метод середины квадрата (Middle-Square Method)

Это – фактически первый алгоритм для генерации псевдослучайных чисел. Он был предложен Дж. фон Нейманом и состоит в следующем: выбирается некоторое 2k-значное число γ0 = 0. e1 e2…e2k и возводится в квадрат, так что

γ02 = 0.d1d2…d4k, при этом, для построения γ1 выбираются

средние 2k цифр последнего результата, то есть γ1 = 0.dk+1 dk+2…d3k. Далее процесс повторяется согласно той же самой процедуре.

Пример 3.1.	Пусть	γ0 = 0,9876 (это	соответствует
случаю k = 2 ).	Тогда γ02	= 0,97535376 и,	следовательно,

γ1 = 0,5353. Для получения γ2 вычисляем γ = 0,24654609, откуда

γ2 = 0.6546 и т.д.

Нетрудно, видеть, что методу середины квадрата соответствует функция

Ψ (x)= {10−2 k [103 k x2]}

или, что то же самое,

Ψ (x)=10−2 [10-2 k {10k x2}] ,

где операция [x] означает вычисление целой части числа x, а {x}, как и раньше, – вычисление дробной части x.

Вскоре после открытия метода середины квадрата было, однако, выяснено, что этот метод весьма далек от

31

удовлетворительного,6 и его применение с большой вероятностью (в зависимости от начальной величины γ0) быстро приведет к значению 0 или, в лучшем случае, к короткой циклически повторяющейся последовательности. В частности, в приведенном выше примере процедура выходит на нулевое значение уже после 50 итераций. Более того, было показано,7 что при удачном выборе γ0, когда процесс не вырождается быстро в чистый 0 или в короткую циклическую последовательность, метод середины квадрата все равно воспроизводит преимущественно маленькие числа, то есть плотность генерируемого распределения весьма далека от равномерной.

Конгруэнтная генерация

Наиболее популярным в практических приложениях оказались методы генерации псевдослучайных чисел на основе кусочно-афинного преобразования8

µn+1 = (aµn + c) (mod M),

µn [0;M–1],

(3.5)

где a, c и M – некоторые целые числа, причем a и M выбираются взаимно простыми. Далее псевдослучайные числа получаются по формуле

γn = µMn .

6См., например, G. E. Forsythe, Generation and testing of random digits at the National Bureau of Standards, In: Monte Carlo method. U. S. Department of Commerce, National Bureau pf Standards, Applied Mathematics Series 12, June 1951, p. 34-35.

7См., например, I. M. Sobol, A Primer for Monte Carlo Method, CRC Press, 1994.

8Для любой пары целых чисел N ≥ 0 и M ≥ 1 символ N (mod M) обозначает

остаток от деления N на M (очевидно, должно выполняться 0 ≤ N (mod M) ≤

≤ M – 1).

32

Заметим, что преобразование (3.5) при любом целом M ≥ 1 сохраняет мощность множества {0, 1,…, M – 1}, поэтому соответствующий генератор называется конгруэнтным генератором.

Постоянная a обычно выбирается достаточно большой, чтобы любые две близкие начальные величины очень быстро пробежали многократно по единичному интервалу и через небольшое число итераций оказались разнесенными друг от друга. Это соответствует тому факту, что график преобразований в соотношении (3.5) изображается множеством почти вертикальных линий (сравните с графиком на рис. 3.3).

Очень часто постоянная c в рекуррентной формуле (3.5) принимается равной нулю, и в этом случае используют термин

“линейный конгруэнтный генератор”. В более ранней литературе можно также встретить название “метод вычетов

(residual method)” или “метод сравнения (congruential method)”. Такой метод восходит к Д. Лемеру.9 Существует обширная литература, посвященная подходящему выбору параметров a и M, но далеко не все источники заслуживают доверия.10 Поэтому неопытному пользователю следует

9См. D. H. Lehmer, Mathematical methods in large-scale computing units, Proc.

2nd symposium on large-scale digital calculating machinery (1949), Harvard Univ. Press, 1951, p. 141-146.

10В начале эпохи своего развития фирма IBM поставляла на рынок

компьютеры со встроенным генератором случайных чисел RANDU, который использовал значения параметров a = 65539, M = 231. Имеется

масса литературных источников, упоминающих о неадекватности этого генератора (см., например, W. H. Press, S. A. Teukolsky, W. T. Welterling, and B. P. Flannery, Numerical Recipes in C, Cambridge Univ. Press, 1992; I.M. Sobol, A Primer for Monte Carlo Method, CRC Press, 1994; G.E. Forsythe, M.A. Malcolm and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1977; S. Tezuka, Uniform Random Numbers: Theory and Practice, Kluwer Academic Press, 1995). Поэтому широко распространено мнение, что следует признавать неудовлетворительными результаты расчетов многих задач, выполненных при помощи генератора RANDU. К сожалению, данный генератор был скопирован во множестве других компьютерных систем, включая вычислительную систему ЕС.

33

руководствоваться советом, который часто можно встретить в литературе: никогда не полагайтесь на генераторы чисел в

виде «черного ящика», которые якобы были протестированы, с какими бы системами они не поставлялись; не доверяйте никакому генератору чисел, по поводу которого вы не сможете найти надлежащую рекомендацию, каким бы сложным и заслуживающим доверия он не выглядел.

С другой стороны, как отмечается в книге И.М. Соболя [18],11 достаточно удовлетворительная последовательность псевдослучайных чисел получается, например, при a = 517, M = 242, µ0 = 1; результаты статистической проверки этих чисел приведены в работе O. Taussky and J. Todd, Generation and testing of pseudorandom numbers, Symposium on Monte Carlo methods, ed. H.A. Meyer, Wiley, New York, 1956, p. 15-28.

Серия генераторов типа Ran

На Западе считается, что книга Пресса, Текольски, Велтерлинга и Фланнери [37] является очень хорошим источником генераторов случайных чисел, которые хорошо проверены и заслуживают доверия. Самый простой из предложенных ими генераторов – Ran0 определяется рекуррентной формулой (3.5) с параметрами a = 75 = 16807, c = 0 и M = 231 – 1. Этот выбор параметров был предложен еще в работе Парка и Миллера12 как минимальный стандартный генератор. Есть некоторые особенности, связанные с трудностями преодоления проблемы округления в умножении

a на µn в (3..5)	для данных значений	параметров	на
32 разрядных	компьютерах – детали	изложены	в

упоминавшейся уже книге Пресса, Текольски, Велтерлинга и Фланнери [37].

11Мы считаем, что этот источник заслуживает самого глубокого доверия.

12См. S. K. Park and K. W. Miller, Random number generations: good ones are hard to find, Communications of the ACM 31 (10) (1998), p. 1192-1201.

34

Ran1 – это улучшенная версия генератора Ran0, использующая алгоритм осторожного перетасовывания случайных чисел. Такая процедура весьма нетривиальна, поскольку перетасовки часто могут привести к прямо противоположной цели.

Ran2 – следующая версия генератора из указанной серии. Она основана на определенной идее сцепления двух линейных конгруэнтных генераторов с последующей целью построить один, но с намного более длинным периодом. Интересующийся читатель может найти детали в работе L’Ecuyer, Efficient and portable combined random number generators, Communications of the ACM 31 (1988), pp. 742-749.

Наконец, Ran3 – наиболее изощренная программа из данной серии генераторов; она основана на субтрактивном методе, предложенном Д. Нутом.13 За деталями мы отсылаем опять же к книге Пресса, Текольски, Велтерлинга и Фланнери [37].

Крутильщик Мерсенна (Mersenne twister)

Одна из наиболее продвинутых на настоящий момент программ генерации псевдослучайных чисел – так называемый крутильщик Мерсенна. Название определено тем, что период последовательности, производимой этим генератором, равен числу Мерсенна – простому числу, представимому в виде 2n − 1 при некотором натуральном n.

Вчастности, для программы, предложенной в работах

M. Matsumoto and T. Nishimura, Mersenne twister: a 623–

dimensionally equidistributed uniform pseudorandom number generator, 199714 и M. Matsumoto and T. Nishimura, Mersenne twister: a 623-dimensionally equidistributed uniform pseudorandom number generator, ACM Transactions on Modeling and Computer

13 См. D. Knuth, The Art of Computer Programming: Seminumerical Algorithms, Vol.2, Addison Wesley, 1981.

14См. http://www.math.keio.ac.jp/_matumoto/emt.html

35

Simulation 8(1) (1988), p. 3-30, период крутильщика Мерсенна равен 219937 − 1. Для этого, чтобы представить себе, что это за

число, отметим, что компьютер, производящий 1 млрд таких чисел в секунду, мог бы работать в течение многих тысяч жизненных циклов солнечной системы среднего размера, измеряющихся от ее начального формирования и до коллапса в черную дыру, прежде чем псевдослучайная последовательность начнет повторять себя. Другими словами, можно считать, что для всех реальных практических нужд этот генератор имеет бесконечный период.

Крутильщик Мерсенна реально основан на объединении очень многих идей, уже развитых к настоящему моменту. Пожалуй стоит процитировать самих авторов:

Крутильщик Мерсенна использует множество существующих идей. В частности, мы благодарны следующим людям: N. Yoneda, P. L’Ecuyer, R. Couture, H. Niederreiter, P. Hellekalek, M. Fushirni, S. Tezuka, Y. Kurita, D. Knuth, H. Leeb, S. Wegenkittl, T. Cooper, M. Rieffel, H. Enomoto и многим другим,

которые дали нам ценные комментарии.

Есть сведения из литературы, что данный генератор проявил себя очень хорошо на тестах.15 В то же время, неизвестны публикации, свидетельствующие о его неудачных испытаниях. Его программный код свободно доступен из Интернета и он работает, как утверждают авторы, не медленнее, чем другие популярные генераторы, уже зарекомендовавшие себя с практической точки зрения. В книге П. Джекела [9] рекомендуется, по крайней мере, иметь его в виду как резервный генератор.

15 Автор данной книги не берет на себя ответственность утверждать, что эти сведения достоверны.

36

Так чем же пользоваться?

К сожалению, многие пользователи методов Монте-Карло не задумываются о роли используемого ими генератора псевдослучайных чисел или ведут себя чересчур доверчиво к автору генератора, который они используют как “черный ящик”. Нельзя утверждать, что генератор случайной последовательности – наиболее сложная часть реализации процедуры Монте-Карло. Но в цепи проблем, связанных с применением методов Монте-Карло, от генератора зависит слишком многое, поэтому надежность используемого генератора является одним из важнейших факторов при моделировании. Ранее в общих чертах были изложены основные принципы генерации, из которых следует, что все генераторы случайных чисел в той или иной мере дефектны. Насколько они подходят для какой-либо конкретной задачи напрямую зависит от самой задачи, по этой причине нет просто хороших или просто плохих генераторов, так как качество их работы может быть оценено только на данной задаче. Конечно, для учебных задач можно не задумываясь использовать генераторы, зашитые в стандартных программных продуктах, применяемых в учебном процессе. Однако при решении больших производственных задач, как считается, крайне желательно иметь в распоряжении некоторую библиотеку различных генераторов и по возможности дублировать расчеты, варьируя используемые генераторы.

3.4 Статистическая проверка случайных чисел

Ранее неоднократно отмечалось, что случайные числа, независимо от способа их получения, необходимо проверять на случайность, прежде чем применять в расчетах. Теперь переходим к обсуждению определенных способов проверки такой случайности. Эти способы основаны на применении методов математической статистики и называются

37

статистическими критериями согласия. Положительный результат проверки по таким критериям – это только необходимое условие для принятия случайных чисел к работе.16 Достаточные условия реально могут быть введены, когда предполагается иметь дело с достаточно узким классом задач. Ниже обсудим всего два статистических критерия согласия – это так называемые критерии χ2 и ω2.

Критерий согласия χ2

Пусть X – некоторая случайная величина, которая может быть многомерной, а кроме того, дискретной или непрерывной.17 Пусть D – множество всевозможных значений случайной величины X и пусть зафиксировано некоторое

разбиение множества D на r попарно дизъюнктных множеств18

D1, D2, …, Dr, то есть19

D = D1 D2 ... Dr , где Int Di ∩Int Dj = , i≠j.

Обозначим также

p		:= P		{X D			,	j=1,2,…,r.
	j				j	}

Очевидно, что p1 + p2 + … + pr = 1.

Пусть далее x1, x2, …, xN – N независимых реализаций случайной величины X и пусть νj – число таких реализаций,

16Обычно в математике “критерий” понимается как синоним термина

“необходимое и достаточное условие”. Однако специалисты по математической статистике не придерживаются этих традиций.

17То есть это случайная величина произвольного вида.

18В контексте данного изложения под дизъюнктными множествами понимаются те множества, которые могут образовывать непустое пересечение только в том случае, когда это пересечение образовано исключительно граничными точками каждого из множеств.

19Операция Int D означает удаление границ у множества D, то есть переход к внутренней части этого множества.

38

принадлежащих множеству Dj. Случайная величина νj подчиняется биномиальному закону распределения с математическим ожиданием M[νj] = N pj и дисперсией D[νj] = N pj (1-pj).20 Соответственно, совокупность случайных величин (ν1, ν2,…, νr) подчиняется мультиномиальному закону распределения, характеризуемому набором вероятностей

	P({ν1 = k1} {ν2 = k2} ... {νr = kr })=		N!		p1k1 p2k2 ... prkr
			k1!k2!...kr!
	при всевозможных целых	неотрицательных			k1, k2,…, kr,
	удовлетворяющих условию k1 + k2 +… + kr = N.				значениях N
	Интуитивно понятно, что	при больших

наблюдаемые на практике значения νj должны приближаться к их теоретическим значениям N pj. В качестве меры рассогласования практических значений с теоретическими удобно выбрать величину21

r	(νj − N pj )2
χN := ∑		.	(3.6)
j =	N pj

20 Действительно, νj это фактически количество наступлений события A := {X Dj} в N независимых испытаниях. Поэтому можно воспользоваться известными из теории вероятностей результатами, относящимися к схеме независимых испытаний Бернулли.

21 Следует всегда различать теоретическую и практическую интерпретации этой формулы. В теории νj понимаются как случайные

величины определенного вида, и поэтому χN имеет смысл случайной

величины. Однако при применении критерия χ2 на практике νj имеют смысл конкретных числовых реализаций соответствующих случайных величин, а

величина χN приобретает тогда конкретное числовое значение, которое и анализируется в ходе применения критерия χ2.

39

Теорема 3.2 (К. Пирсон)

Какова бы ни была случайная величина X и фиксированное разбиение D = D1 D2 … Dr (такое, что все pj > 0, j = 1, 2,…, r), при произвольном фиксированном x > 0 имеет место предельная формула

lim P({χN2	< x})= ∫0xkr −1(t)	t ,
N →∞

где km(x) – плотность распределения χ2 с m степенями свободы, определяемая формулой22

m

m

−

m

−1

x

e 2 .

x 2

km (x)=

2 Γ

2

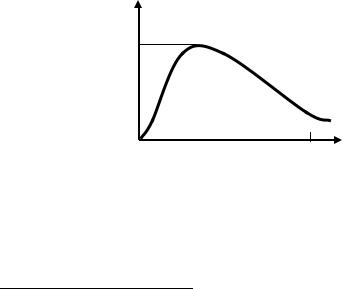
Примерный график χ2-распределения при m = 6 приведен на рис. 3.4.

у

у=k6(х)

0,125

0

1,0

x

Рис.3.4. График функции k6(x)

Теорему К. Пирсона часто используют в статистике для проверки гипотез о законе распределения случайной величины. Набор соответствующих условий, позволяющих принять или

22 Здесь Г(x) – гамма-функция.

40