Башуров Методика решения математических задач 2011

УДК 517

ББК 22.16 Б 33

Башуров В.В., Комлева И.А. Методика решения математических задач: Учебно-методическое пособие. М.: НИЯУ МИФИ, 2011. – 140 с.

В пособии дается методология поиска алгоритма решения задач по таким разделам математики, как последовательности; функции; частные производные, производные от неэлементарных функций; исследование функций и нахождение экстремумов; определенные, двойные и тройные интегралы, интегралы, зависящие от параметра; кратные и криволинейные интегралы; поверхностные интегралы и элементы векторного анализа; дифференциальные операторы; обыкновенные дифференциальные уравнения.

Данное пособие предназначено для студентов специальностей: 230101.65 – Вычислительные машины, комплексы, системы и сети, 200101.65 – Приборостроение, 151001.65 – Технология машиностроения Пособие подготовлено в рамках Программы создания и развития

НИЯУ МИФИ.

Рецензент О.В. Нагорнов

ISBN 978-5-7262-1306-4 © Национальный исследовательский ядерный университет «МИФИ», 2011

_______

3

ПРЕДИСЛОВИЕ

Настоящая книга состоит из 10 глав. Каждая глава включает краткую теоретическую часть, примеры решения задач и задачи для самостоятельного решения по разделам курса математики, полностью соответствующим Государственному стандарту по специальностям 230101.65 – Вычислительные машины, комплексы, системы и сети, 200101.65 – Приборостроение, 151001.65 – Технология машиностроения.

Теоретическая часть – это краткий справочник, содержащий все нужные для решения задач формулы и теоремы. В примерах решения задач приведен достаточно подробный анализ с использованием методологии поиска алгоритма этого решения. Большинство из задач как приведенных в примерах, так и для самостоятельного решения на протяжении многих лет используются нами в качестве экзаменационных.

Построение пособия в чем-то напоминает сборник «Задачи и упражнения по теории вероятностей»1, но в нашем пособии раскрывается методология поиска алгоритма решения предложенных задач. Это отличает настоящее пособие от многочисленных сборников задач, пособий по тому или иному разделу математики (сразу прошу прощения у тех авторов, труды которых мне не попадались, но еще Козьма Прутков говорил, что нельзя объять необъятное).

Если бы мы были уверены, что нас не упрекнут за излишнюю смелость в использовании терминов, и что мы не внесем путаницу в библиотечные классификаторы, мы бы могли назвать настоящую книгу, например, так: «Психология нахождения решения задач в курсе высшей математики для инженерных факультетов». Рассуждения по этому поводу мы нашли в книге Ж. Адамара, имеющей в русском переводе название «Исследование психологии процесса изобретения в области математики», вышедшей в московском издательстве МЦНМО в 2001 году (оригинал появился в Париже в 1959 году). Если вы слово «изобретения» замените

1 Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: Учеб. пособие для студ. втузов. – 3-е изд., исправленное. М.: Изд. центр «Акаде-

мия», 2000.

4

словами «решения» или «поиск решения», то многое из этой книги можно отнести к построению и содержанию настоящей книги. Но и это название не передает полностью содержания книги.

Как это ни странно, но ближе всего структуру настоящей книги, ее язык и комментарии к приводимым формулам, примеры подробно решенных задач передает игра «Лего». Там из простейших элементов требуется составить заданную фигуру (т.е. решить задачу). В этой игре присутствуют все элементы рассуждений, которые наличествуют при поиске решения математических задач, – анализ задачи (рисунка), анализ имеющихся средств решения этой задачи (набор элементов в игре), составление схемы решения (мы его называем «третий этап решения задачи», а в игре этому этапу соответствует мысленное составление отдельных фрагментов заданного рисунка).

Однако подобрать название книги по этой аналогии было бы очень трудно и непривычно (все-таки мы пишем книгу по математике, да еще для студентов). Назвать книгу учебником мы не имеем право – в этой книге нет доказательств ни одной теоремы или формулы. Более того, если бы структура книги, ее язык и методология решения задач была похожа на множество учебников, в которых излагается, по сути, одно и то же, то мы бы не принялись за написание настоящей книги – вряд ли мы добавили что-нибудь новое в бесконечный океан математики.

Решение любой задачи, с точки зрения психологии, можно разбить на пять этапов.

Этап 1. Классификация задачи. Выполнение этого пункта помогает уточнить, сузить круг возможных для решения задачи формул и теоретических результатов.

Этап 2. Справочное бюро. В каждой главе этому названию соответствует первый параграф с названием «Определения, основные теоремы и формулы». В нем помещены те формулы, которые могут понадобиться для решения задач, а также, возможно пригодные, теоретические результаты. Пользуясь этим «справочным бюро», можно как бы отсечь все «лишние» формулы и теоремы, резко сужая круг полезных для решения данной задачи формул и приемов.

Этап 3. Построение схемы решения. С помощью «справочного бюро» мысленно строится алгоритм решения, при этом разрешаются все возникающие вопросы. В результате алгоритм будет построен от начала до конца, разбитый на отдельные блоки, реализация каждого из которых представляет чисто техническую задачу. На этом этапе требуется минимальное участие карандаша, ручки или мела.

5

Этап 4. Реализация построенного на предыдущем этапе алгоритма решения. На этом этапе происходит оформление решения на бумаге, т.е. вы детально оформляете все, что до этого было построено у вас в голове, с «расписыванием» каждого блока.

Этап 5. Проверка. На этом этапе реализуется ваше умение анализировать полученное решение, обнаруживать его несоответствие тому классу объектов, которому изначально должно принадлежать решение. Это изначальное представление о принадлежности решения тому или иному классу, множеству или еще чему-то формируется на втором этапе. Не реализовав второй этап, вы просто-напросто не имеете возможности анализировать полученное решение. Понятно, что проверка принадлежности полученного решения нужному классу не является исчерпывающей – мы привели этот способ как пример.

Использование указанной схемы поиска алгоритма решения задач, предлагаемых на экзаменах, позволяет почти гарантировать их успешное решение.

Не абсолютизируйте предложенную методологию! Но все решения, которые мы приводим в качестве образца решения задач, построены по указанной выше схеме. При этом мы предполагаем, что читатель владеет логикой рассуждений, знаниями математики в объеме средней школы и прослушал курсы (или еще слушает) высшей математики в объеме программы, определяемой Государственным стандартом.

Подбор рекомендуемой литературы, приводимый в конце каждой главы, основан на той литературе, которая есть в библиотеке институтов, в которых работают авторы этой книги. Понятно, что этот подбор далек от идеала как по годам издания, так и по «номенклатуре». Каждое учебное заведение вправе (более того, обязано) пересмотреть этот список с учетом традиций и каталога своей библиотеки.

Авторы выражают искреннюю благодарность преподавателю филиала МИФИ Сергею Викторовичу Жаринову без которого эта книга не появилась на свет за такие, на наш взгляд, короткие сроки, и за неоценимую помощь в создании электронного варианта книги.

6

Глава 1. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

1.1. Определения, основные теоремы и формулы

Определение 1.1. Числовой последовательностью называется однозначное соответствие множества натуральных чисел какому-то множеству действительных чисел N.

По сути дела, последовательность – это функция, заданная на множестве N.

Обозначение последовательности:

{an}, n N, или а1, а2, ..., ап, ...

В этом случае an называется «общим членом» и, как правило,

задается некоторой формулой. В дальнейшем для краткости будем опускать слово «числовые» и просто использовать термин «последовательности».

Выбрасывая из последовательности {ak} конечное или бесконечное «число» членов (но так, чтобы осталось бесконечное же число членов), получим новую последовательность, которую называют подпоследовательностью последовательности {ak} и часто обозначают {ank }.

Определение 1.2. Последовательность {an}, n N , называется ограниченной сверху (снизу), если выполняется неравенство an < A (an > B) для всех членов последовательности {an}, n N .

Определение 1.3. Последовательность {an}, n N , называется ограниченной, если она одновременно ограничена сверху и снизу.

Определение 1.4. Последовательность называется монотонной, если для всех п выполнено неравенство an 1 an (либо an 1 an ).

Определение 1.5. Последовательность {an}, n N , называется сходящейся, если существует такое число a , что для любого > 0 найдется такой номер N , что для всех n > N выполнено неравенство |an a |< . Если такого числа не существует, то последовательность называется расходящейся. Число a называется пределом последовательности {an}, n N, и обозначается как

7

lim an = a . При этом символ n в обозначении предела можно

n

опускать, поскольку ни к чему другому, кроме бесконечности, n стремиться не может. Так же будем опускать символ n N .

Примеры последовательностей, пределы которых «очевидны» и которые мы будем называть «эталонными»:

1)1,1,1,... – предел равен 1;

2)1,1,1,...,1,... – предел равен нулю;

lim an = . Символ указывает на неограниченный рост членов

n

последовательности по мере увеличения номера n.

Набор эталонных пределов в процессе обучения, решения задач может (и должен) пополняться. Вся премудрость отыскания пределов последовательностей сводится к тому, что данная вам для решения последовательность преобразуется так, что она приводится к «эталонным» последовательностям. Приведем сводку теорем, позволяющих производить такие преобразования.

Теорема 1.1. Если две последовательности {an} и {bn} имеют

соответственно пределами a и b , то:

1)lim(an bn) = a b ;

2)lim(an bn) = a b ;

3)если b 0, то lim an = a . bn b

Теорема 1.2. Если для трех последовательностей {an}, {bn}, {cn} для всех п выполняются неравенства an bn cn и

последовательности {an} и {cn} сходятся к одному и тому же пределу, то и последовательность {bn} сходится к тому же пределу.

8

Эта теорема, по традиции ленинградской школы математиков, носит название «теоремы о двух милиционерах».

Теорема 1.3. Если последовательность {an} сходится к пределу a , то и любая ее подпоследовательность сходится к тому же пределу.

Теорема 1.4. Ограниченная монотонная последовательность имеет предел.

Эта теорема важна в том случае, когда существование предела не очевидно, а его существование необходимо для применения теоремы 1.1.

В том случае, если одновременно a = 0 и b = 0, то предел в

выражении an определить при помощи теоремы 1.1 невозможно и bn

если, начиная с некоторого номера N , все члены последовательности {bn} отличны от нуля, то про

последовательность an говорят, что она задает неопределенность

bn

0 , а нахождение предела такой последовательности называется

0

«раскрытием неопределенности вида 0 ». 0

Кроме неопределенности вида 0 , существуют неопределенно- 0

сти вида: , , 0 , 1 и др.

Для практики в случае непрерывности функции определенной для всех an и a полезна формула

lim f (an )= f (a),

где a – предел последовательности {an}.

В ряде случаев последовательность может быть задана рекуррентным соотношением an 1 = f (an ), а а1 – некое, начально задаваемое, число.

9

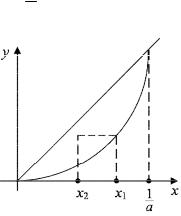
Для нахождения предела заданной последовательности, таким образом, полезна не упоминаемая ни в одном учебнике теорема, доказанная в 1966 году одним из авторов [1]. Суть ее заключается в том, что если задана рекурсия an 1 = f (an ), функция f (x)

непрерывна на промежутке [ , ] и переводит сегмент [ , ] сам в

себя, то для сходимости рекурсии, начинающейся с любой точки промежутка [ , ] необходимо и достаточно, чтобы множества

корней уравнений x = f (x) и x = f ( f (x)) совпадали. В этом

случае рекурсия сходится к какому-то корню уравнения x = f (x) .

Немного поговорим о важности этой теоремы. Рассмотрим

x = 1 ). Следовательно, рекуррентное соотношение определяет по-

следовательность {xn}, сходящуюся к корню (единственному на

10