Борман Теория каскадов для разделения бинарных 2011

Считая, что ci+, f = ci−, f , где индексы + и – означают, что соответ-

ствующие величины взяты из решений для отборной и отвальной частей каскада, и, раскрывая это равенство с помощью соотноше-

ний (2.162) и (2.170), получим

ciP

ck , f

RP

αi −1

ciW

ck , f

RW

αi −1

1

−

nk

R f

1−

nk

R f

c

c

kP

nk

=

kW

nk

,

(2.173)

1− RnkP

1− RnkW

αi −1

R

f

αi −1

f

R

nk

nk

где R f

=

cn, f

.

nk

ck , f

Выражение (2.173) легко приводится к виду

RP

αi −1

RW

αi −1

4PciP 1−

nk

R f

4WciW 1−

nk

R f

nk

nk

= −

.

(2.174)

4P

c

−

c

4W

c

nW

−

c

nP

kP

kW

ε

c

ε

c

nk

c

k , f

nk

c

n, f

n, f

k , f

Нетрудно убедиться, что в знаменателях (2.174) стоят выражения для «головного» потока каскада Lf, то есть

4P

c

c

4W c

c

Lf

=

nP

−

kP

=

nW

−

kW

.

(2.175)

ε

c

ε

c

c

nk

c

nk

n, f

k , f

n, f

k , f

Учитывая выражение (2.175) и условие несмешения по относительной концентрации Rnk в точке подачи питания ( Rnkf = RnkF ), из

(2.174) имеем

RP

αi −1

RW αi −1

PciP 1

−

nk

=WciW

nk

−1 .

(2.176)

F

F

R

R

nk

nk

Воспользовавшись

условием

покомпонентного

баланса

PciP +WciW = FciF , находим

211

− RW αi −1 1 nk

RnkF

PciP = FciF	RP	αi −1
	nk
	F
	Rnk

	RW	αi −1 .	(2.177)
−	nk
	F
	Rnk

m

Поскольку ∑ Pcj

= P , то

j=1

RW αi −1

m

RW αj −1

1−

RF

1−

RF

nk

nk

ciP

= ciF

nk

∑cjF

nk

(2.178)

αi −1

αi −1

α j −1

RW

α j −1

RP

−

RW

j=1

RP

nk

nk

nk

−

nk

F

F

F

F

Rnk

Rnk

Rnk

Rnk

Аналогично для концентраций в отвале имеем

				RP			αi −1
		1−		nk
				F
ciW = ciF				Rnk
		RP	αi −1					RW		αi −1
		nk		−				nk
		F						F
		Rnk						Rnk

Учитывая,

P	F		εnk SP		,	W
Rnk	/ Rnk	= exp	2			Rnk

RP

αj −1

1−

nk

m

F

∑cjF

Rnk

.(2.179)

α j −1

α j −1

j=1

RP

−

RW

nk

nk

F

F

Rnk

Rnk

что

F

εnk SW

/ Rnk = exp

−

, а

также ис-

2

пользуя обозначения (2.167), выражения (2.178) и (2.179) можно представить в виде

				exp(Qi SW ) −1		m
ciP		= ciF				/ ∑cjF ×
				exp(Qi SW ) −exp(−Qi SW )
						j=1	(2.180)
			exp(Qj SW )−1			,
×
	exp(Qj SW )−exp(−Qj SW )

212

			1−exp(Qi SP )		m
ciW		= ciF			/ ∑cjF ×
			exp(Qi SW ) −exp(−Qi SP )
					j=1	(2.181)
		exp(Qj SP )−1			.
×
	exp(Qj SW )−exp(−Qj SP )

Выражения (2.180), (2.181) совпадают с соответствующими формулами (2.107), (2.108), полученными для Q-каскада [12]. Действительно, каскад с несмешением по относительной концентрации

Rnk = cn для выбранной пары компонентов n и k является частным ck

случаем «свободного» каскада, когда константы Qi задаются в виде

(2.132).

В отдельных случаях может оказаться, что в каскаде с несмешением по относительной концентрации Rnk для одного из компо-

нентов, например, с номером t оказывается, что αt =1, то есть

2εnt = εnk и, соответственно, Qt = 0 .

В этом случае предельный переход приводит к следующим ре-

зультатам
lim	exp(Qt SW ) −1	=	SW	,
	exp(Qt SW ) − exp(−Qt SP )		SP + SW
Qt → 0				(2.182)
	1 − exp (−Qt SP )		SP
lim		=
	exp(Qt SW ) − exp(−Qt SP )		SP + SW

Qt → 0

и, следовательно, соотношения (2.180), (2.181) могут быть переписаны в виде

для i ≠ t :

213

exp(Qi SW ) −1

m

ciP

= ciF

/ ∑cjF ×

exp(Qi SW ) −exp(−Qi SP )

j

=1

exp(Qj SW )−1

j

≠t

S

×

+ctF

W

,

exp(Qj SW )−exp(−Qj SP )

SP + SW

1−exp(−Qi SP )

m

ciW

= ciF

/ ∑cjF ×

exp(Qi SW ) −exp(−Qi SP )

j=1

1−exp (−Qj SP )

j≠t

SP

×

+ctF

,

exp (Qj SW )−exp(−Qj SP )

SP + SW

для i = t :

exp(Qj SW ) −1

S

m

ctP = ctF

W

/ ∑cjF

+

SP

+ SW

exp(Qj SW ) −exp(−Qj SP )

j=1

+ctF

SW

,

S

P

+ S

W

1− exp(−Qj SP

)

SP

m

ctW

= ctF

/ ∑cjF

+

SP

+ SW

exp(Qj SW ) −exp(−Qj SP )

j=1

+ctF

SP

.

S

P

+ S

W

(2.183)

(2.184)

(2.185)

(2.186)

Рассмотрим теперь решение системы (2.141), когда компоненты с номерами n и k являются основными, а остальные примесными

(минорными) [3, 14], т.е. cn

Обозначив cn = c, ck =1−c нение

dcdl = −εnk c(1−c)

+ck ≈1, ci << cn ,ck при i ≠ n,k . , для концентрации c получим урав-

−c ∑ εnjcj +	2P (cP	−c)	.	(2.187)
	L
j≠n,k

214

Так как ci << cn , ck и εnj		порядка εnk , уравнение (2.187)
можно переписать, опуская члены второго порядка малости,
dc	= −εnk c(1	−c) +	2P (cP	−c)	.	(2.188)
dl			L

Уравнение (2.188) является обычным уравнением разделения 2- компонентой смеси. Для примесных (минорных) компонентов,

учитывая условие cn + ck ≈1 , можно записать
	dc	= −c	ε		c −c ε		(1−c) +	2P (cip	−ci )
	i			in		ik				. (2.189)
	dl	i			i			L

Рассмотрим каскад с несмешением по относительной концен-

трации R =	cn	=	c	. В этом случае
nk	ck	1− c
							4P (cP −c)
					L =						(2.190)
и							εnk c(1−c)
					dci			εnk
							= −		c(1 − c) .		(2.191)
					dl
							2

В уравнении (2.189) перейдем от независимой переменной l к переменной c, полагая

dcdli = dcdci dcdl .

Учитывая (2.190) и (2.191), из (2.192) и (2.189) получаем

dc

2ci,P

ε

in

ε

ε

nk

c

i

−

+

ik +

= −

iP

.

εnk

cP −c

dc

1−c

c

2(cP −c)

(2.192)

(2.193)

Решение линейного уравнения (2.193) с очевидным граничным

условием ci (c)		c=c P	= ciP имеет вид
				c(1−c)		R−di − R−di
		c	= c					,	(2.194)
		i	iP λi (cP −c)				P
				215

где R =

c

,

R =

cP

,

Q = εin +εik ,

Q =

εnk

.

1−c

P

1

−cP

i

2

n

2

Уравнения для отвальной части каскада имеют тот же вид, что и уравнения (2.189), (2.193), но вместо концентраций ciP в них входит концентрация примесных (минорных) изотопов в потоке отвала ciW, а вместо потока отбора P – поток отвала W. При этом решение уравнения для отвальной части каскада с граничным условием

ci (c)

c=cW = ciW имеет вид

c(1−c)

R−di − R−di

c

= c

,

(2.195)

i

iW λi (c −cW ) W

где R =

cW

.

1

−c

W

При сделанных предположениях можно считать, что в точке подачи питания c = cF . Пользуясь условием неразрывности концен-

траций в точке подачи питания c (c)		c отбора	= c (c)		c отвала	, под-
i		c=cF	i		c=cF

ставляя в (2.194) и (2.195) вместо c концентрацию cF и разделив

(2.194) на (2.195), получим

1 =	c c			F	−c			R−di − R−di
	iP				W			F	P	,	(2.196)
	c c			P	−c	F	R−di − R−di
	iW							W	F

где RF = 1−cFcF .

Из соотношения (2.196) получаем выражение, связывающее концентрации минорных изотопов в потоке отвала и отбора

ciW

= ciP

c

F

−c

R−di

− R −di

W

F

P

.

(2.197)

c

P

−c

F

R−di

− R −di

W

F

Подставляя соотношение (2.196) в уравнение баланса

c

=

cP −cF

c

+

cP −cW

c

,

(2.198)

iF

cF −cW

i,P

iW

cF −cW

где ciF , i ≠ n,k – концентрация i-го примесного изотопа в потоке питания, можно получить выражения для расчета концентрации

216

примесных изотопов в потоках отбора и отвала в зависимости от их содержания в потоке питания и концентрации основных компонентов в потоках отбора, отвала и питания

ciP = ciF

c

P

−c R−di − R −di

,

W

W

F

c

F

−c

R−di − R −di

W

W

P

.

(2.199)

ciW = ciF

c

P

−c

R−di − R −di

W

F

P

c

P

−c

F

R−di − R −di

W

F

Формула (2.199) могут быть использованы для предварительной оценки содержания примесных изотопов в отбираемых из каскада потоках, исходя из заданных величин внешних потоков (подаваемых и отбираемых) и содержания в них основного (целевого) компонента, например, изотопа 235U при обогащении урана, а также содержания примесных изотопов в подаваемом потоке.

2.3.4.4.Расчет R-каскада с дополнительным потоком отбора [3, 15]

Задачи разделения многокомпонентных смесей в R-каскадах, как правило, связаны с определенными практическими соображениями. Так, например, практическая польза от результатов расчета каскада для разделения многокомпонентных изотопных смесей с несколькими отборами связана с тем обстоятельством, что распределения концентраций компонентов с промежуточными массами имеют максимальные значения внутри каскада и, следовательно, существует возможность получить в дополнительном отборе концентрацию промежуточного компонента, большую, чем в потоке основного отбора на концах каскада.

Рассмотрим для определенности каскад произвольного профиля. В некоторых точках каскада производится отбор смеси или подача питания. Будем считать, что каскад состоит из конечного числа участков непрерывного профиля. В точках разрыва профиля, а также в точках отбора смеси и подачи питания происходит разрыв параметров каскада. Назовем часть каскада, заключенную между двумя соседними точками разрыва параметров, секцией. Обозначим B полное число секций в каскаде и b – порядковый номер сек-

217

ции. Каждая секция состоит из Sb последовательно соединенных разделительных ступеней.

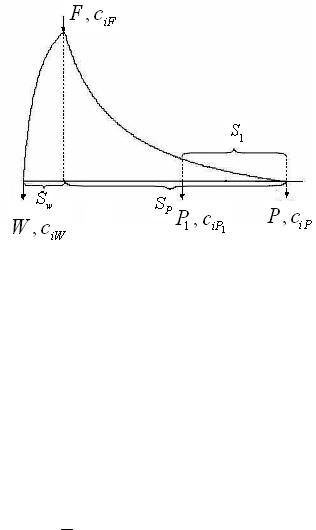
Рис. 2.8. Принципиальная схема R-каскада с дополнительным отбором

Нумерацию секций и ступеней в секции ( 0 ≤ s ≤ Sb ) будем вес-

ти в направлении от «легкого» конца каскада (основного отбора) к «тяжелому» концу (отвалу). Обобщая для рассматриваемого случая соотношение (2.95), можно написать:

Lb (s)C (s) =

i

b P Cr

s

Lb (0)Cb (0)

+2

(0)

r (0)

∫

φ (t)dt

(2.200)

− F C

i

∑

r i

r i

i

=

r =1

0

,

φi (s)

i =1,..., m ,

где Pr и Fr – потоки отбора и питания соответственно в начале секции r ; Cir (0) – концентрация i-го компонента в соответствующей точке отбора; Cir (0) – концентрация i-го компонента в соответствующей точке питания.

218

Конкретизируем систему (2.200) для частного случая каскада с двумя точками отбора и характеристической функцией

ϕi = exp(Qi s) (рис. 2.8).

Считая, что поток L(s) непрерывен по каскаду, а на его концах обращается в нуль, и используя (2.200), получаем:

LP CiP

= 2PCiP

1− exp(−Qi S1 )

,

(2.201)

1

1

Qi

L C

= 2PC

1−exp(−Qi S1)

+

f i, f

iP

Qi

(2.202)

1−exp −Q

S

− S

P

+2PC

i (

1 )

,

1

iP1

Qi

L f Ci, f

= 2WCiW

exp(Qi SW ) −1

,

(2.203)

Qi

где P,W , P1 – потоки основного отбора, отвала и дополнительного

отбора, соответственно; CiP ,CiW

,CiP

– концентрации i-го компо-

1

нента в этих потоках;

L f ,Cif – поток и концентрации i-го компо-

нента в сечении ввода питания; SP , SW – числа ступеней в отбор-

ной и отвальной частях каскада; S1 – число ступеней между точка-

ми дополнительного и основного отборов.

Пусть в каскаде имеет место несмешение относительных кон-

центраций R	n,n+1	=	Cn		, т.е. каскад «идеальный» по компонентам
			Cn+1
с номерами n и n+1.
Тогда				RnP,n+1
							= exp(Qn S1 ),	(2.204)
				RnP,1n+1
				RnP,n+1			= exp(Qn SP ),	(2.205)
				RnF,n+1
						219

	RW
	n,n+1	= exp(−Qn SW ).	(2.206)
	RnF,n+1

Комбинируя соотношения (2.202), (2.203) с учетом (2.206) и

уравнений баланса

P1

F

=

+

W

+1,

(2.207)

P

P

P

F

C

=

P1

C

iP

+ W C

iW

+C ,

(2.208)

P

iF

P

P

iP

1

i = 1,..., m,

получим

P	−di	+	P	P	−di	+
CiP (Rn,n+1 )			1	CiP (Rn1,n+1 )
			P	1		(2.209)
+W CiW (RnW,n+1 )−di − F CiF (RnF,n+1 )−di ,
P				P

i ≠ n, n +1.

Величины внешних потоков с помощью уравнений (2.207), (2.208) могут быть выражены через концентрации целевого компо-

нента в них и отношение P1 P :

F

c

nP

−c

cnP

−cnW

P

nW

1

1

=

−

,

(2.210)

P

c

−c

c

−c

P

nF

nW

nF

nW

W

=

F

−

P1

−1.

(2.211)

P

P

P

Решая систему уравнений (2.208) – (2.209) относительно концентраций ciP и ciW с учетом уравнений (2.210) и (2.211) и условия

m

∑ c j =1, находим j =1

220