Загребаев Методы обработки статистической информации в задачах контроля 2008

Пусть квадратная матрица T(i) имеет вид

	i					−1
T(i) =	κ∑		( j)		т( j) + U	,
		t		t
	j=1

где κ – скаляр; t ( j) – вектор; U – постоянная симметричная мат-

рица той же размерности, то справедливо следующее рекуррентное соотношение:

т(i)T(i −1)

T(i) = T(i −

1) −

T(i −1)t

(i)t

,

κ−1 + t

т(i)T(i −1)t(i)

T(0) = U−1 .

Полагая

T(i) = Γ(i) ; T(i −1) = Γ(i −1) ;

∞

κ = − ∫F ′(η) f ′(η)dη;

−∞

∂ψ( j,c )

t (i) =

;

U = 0 ,

∂c

ˆ

c

=ci−1

получим для коэффициента усиления Γ(i)

следующее рекуррентное

выражение :

Γ(i) = Γ(i −1) −

∂

т

Γ(i −1)

∂ψ(i,c )

ψ(i,c )

Γ(i −1)

ˆ

∂c

∂c

ˆ

c =c

−

i−1

c

=ci−1

. (3.4.42)

∞

′

′

−1

∂

т

−

∫

+

ψ(i,c )

Γ(i −1)

∂ψ(i,c )

F (η) f

(η)dη

−∞

∂c

ˆ

∂c

ˆ

c

=c

c

=ci−1

i−1

В качестве начального приближения принимают матрицу

Γ(0) = νI ,

(3.4.43)

где ν – большое число.

Таким образом, оптимальный рекуррентный алгоритм будет состоять из двух вычисляемых формул

ˆ ˆ	′	ˆ	∂ψ(i,c )
ci = ci−1						,	(3.4.44)
	+ Γ(i)F (ε(i,ci−1)))		∂c
						ˆ
					c	=ci−1

221

где Γ(i) вычисляется на каждом шаге рекуррентного процесса по формуле (3.4.42) при начальных условиях (3.4.43). Начальное при-

ˆ

ближение c0 может быть задано любым вектором соответствую-

щей размерности.

В заключение данного раздела запишем рекуррентный оптимальный алгоритм для линейного динамического объекта

n	n	n
y(i) = −∑a j y(i − j) + ∑ bk u(i − k) + ∑dl η(i −l) .
j=1	k=0	l=0

Как известно, оптимальная настраиваемая модель, соответствующая данному объекту, имеет вид:

n					n
y(i) = −∑a j y(i − j) + ∑ bk u(i − k) +
j=1					k=0
n
+∑	dl	( y(i	−l) − y(i −l)) ,
l=1 d0
или, используя введенные в разд. 3.1.1 обозначения,
~					т ~
	y(i) = z(i)				c .
Тогда
~
	∂ψ(i, c )			= z	(i) .	(3.4.45)
~
		∂c

Подставляя (3.4.45) в рекуррентные соотношения (3.4.42), (3.4.44), получим:

ˆ

ˆ

′

ˆ

(3.4.46а)

c(i) = c(i −1) + Γ(i)F (ε(i, c(i −1)))z(i) ;

Γ(i) = Γ(i −1) −

Γ(i −1)z (i)z т(i)Γ(i −1)

,

∞

′

′

−1

т

∫

−

F

(η) f (η)d

η

+ z (i)Γ(i −1)z (i)

−∞

~

т

ˆ

(3.4.46б)

ε(i, c (i −1)) = y(i) − z

(i)c(i −1) ,

ˆ

– любой вектор; Γ(0) = λI ; λ – большое число.

где c(0)

222

3.4.5.Оптимальная функция потерь

Впредыдущем разделе была получена формула, которая отражает зависимость АМКО от функции потерь F(η) и плотности

распределения шумов f (η) при оптимальном (в смысле минимума АМКО) выборе матрицы B

		∞
		∫ F′2 (η) f (η)dη					A−1	(c,ση2 ).
V(F, f ) =	−∞
						2
		∞	′	′
		∫	F (η) f
				(η)dη
	−∞

Будем считать, что плотность распределения ошибок измерений известна. Тогда поставим задачу подобрать такую функцию потерь F * (ε) , которая обеспечит минимальное значение АМКО.

Для решения этой задачи отметим, что любую функцию потерь можно представить в виде суммы F *(ε) + λδF(ε) , где δF(ε) –

малая вариация функции потерь, λ – скалярный множитель. Тогда АМКО будет функцией скалярного параметра λ и плотности распределения f (η) . Учитывая, что f (η) определена природой шума,

АМКО будет функцией только одного параметра λ:

ϕ(λ) = V(F * (ε) + λδF(ε), f ) .

В этом случае условие экстремума АМКО имеет вид:

ϕ′(λ) λ=0 = 0 .

Рассмотрим, что представляет собой матрица ϕ(λ):

ϕ(λ) = V(F * +λδF, f ) =

∞

′2

∞

′

′

2

∞

′2

∫

∫

∫

f (η)F * (η)dη+ 2λ

f (η)F * (η)δF (η)dη+ λ

×

f (η)δF (η)dη

−∞

−∞

−∞

∞

2

∞

∞

∫

′

′

∫

′

′

∫

′

′

+ 2λ

f (η)F * (η)dη

f (η)δF (η)dη+

×

f (η)F * (η)dη

−∞

−∞

−∞

∞

2

−1

×A−1 (c ,ση2 ).

+λ2

∫ f

′(η)δF ′(η)dη

−∞

223

Тогда

∞

∞

2

′

=

′

′

′

′

−

ϕ (λ)

λ=0

2

∫

f (η)F * (η)δF (η)dη

∫

f (η)F * (η)dη

−∞

−∞

∞

∞

∞

′2

∫

′

′

∫

′

′

∫

−2

f (η)F * (η)dη

f (η)δF (η)

f

(η)F * (η)dη ×

−∞

−∞

−∞

∞

4

−1

(c

∫ f

′

′

×A

−1

2

×

(η)F

* (η)dη

,ση )= 0 .

−∞

Принимая во внимание,

что A−1 (c,ση2 )

не нулевая матрица, и

∞

f

′

′

, получим

допуская, что

∫

(η)F * (η)dη ≠ 0

−∞

∞

′

′

∞

′

′

∫ f (η)F * (η)δF (η)d

η ∫

f

(η)F * (η)dη =

−∞

−∞

∞∞

=∫ f ′(η)δF′(η)dη ∫ f (η)F *′2 (η)dη.

−∞ −∞

Преобразуя последнее выражение, можно записать:

∞	′	′		∞	f	′	′
∫ f	(η)F * (η)δF (η)dη			∫		(η)δF		(η)dη
−∞			−	−∞					= 0 .
∞				∞			* ′
∫	′2	(η)dη		∫	f	′		(η)dη
	f (η)F *					(η)F0
−∞				−∞

Внесем интегралы, стоящие в знаменателях, под интегралы числителей, тогда получим

∞	f	′	′		∞		f	′	′
∫		(η)F * (η)δF (η)		dη =	∫				(η)δF (η)	dη .
	∞					∞		′
−∞	∫	′2	(η)dη		−∞	∫	f		′
		f (η)F *						(η)F * (η)dη
	−∞					−∞

224

Так как δF ′(η) может быть любой функцией, то

	′				f	′
	f (η)F * (η)		=			(η)	,	(3.4.47)
∞	′2			∞	′	′
∫		(η)dη		∫ f
	f (η)F *				(η)F * (η)dη
−∞				−∞

или, после умножения обеих частей (3.4.47) на F *′(η) , получим

	′2	(η)		f	′	′
	f (η)F *		=			(η)F * (η)	.	(3.4.48)
∞	′2			∞
					′	′
∫		(η)dη		∫ f
	f (η)F *				(η)F * (η)dη
−∞				−∞

Нетрудно заметить, что последнее выражение представляет собой равенство нормированных функций. Это равенство справедливо только в том случае, если сами функции пропорциональны. Таким образом, получаем

f (η)F *′2 (η) = k1 f ′(η)F *′(η) ,

где k1 – коэффициент пропорциональности. Отсюда следует, что

F *′(η) = k1 ff ′((η)) ,

η

т.е.

F *′(η) = k1 ff′((η)) = k1{ln f (η)}′.

η

И, следовательно, оптимальная функция потерь определяется соотношением:

F* (ε) = k1 ln f (η) η=ε + k2 .

Впоследнем выражении неопределенными оказываются коэффициенты k1 и k2 . Для их определения рассмотрим графики типо-

вых плотности распределения шума η и логарифма от плотности распределения (рис. 3.5).

Как правило, плотность распределения f (η) является четной функцией, а логарифм плотности распределения – четная убывающая функция, имеющая максимальное значение при η = 0. Таким

225

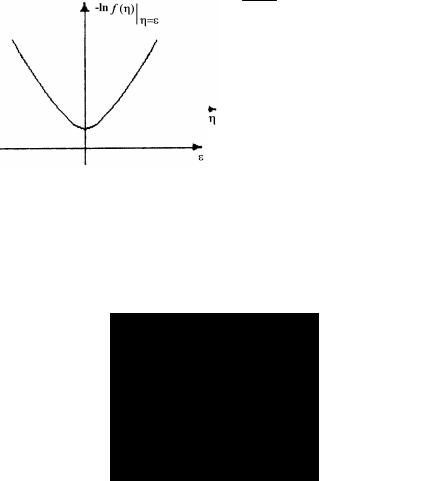
образом, для того, чтобы F ′* (ε) = k1 ff ′((ηη)) имела смысл функции

потерь, т.е. имела минимум при ε = 0 (что эквивалентно η = 0), необходимо условие k1 < 0 (рис. 3.6).

а		б

Рис. 3.5. Типичный вид плотности распределения (а) и логарифма плотности распределения шума η (б)

Рис.3.6. График зависимости функции потерь от невязок ε при k1 < 0 и k2 > 0

Что же касается параметра k2 , то он определяет минимальное значение F * (0) . При k2 > k1 ln f (0) всегда выполняется неравенство F * (ε) > 0 .

Таким образом, оптимальная функция потерь не единственна, а зависит от параметров k1 и k2 . Этот факт является следствием того, что АМКО зависит не от F(ε) , а от F ′(ε) .

226

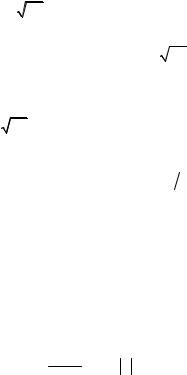
Для задач идентификации конкретные значения этих параметров несущественны. Удобно принять k1 = −1, а k2 = 0 . Таким об-

разом, оптимальная функция потерь равна логарифму плотности распределения помех с обратным знаком:

F * (ε) = −ln f (η)		η=ε .	(3.4.49)

Сравнивая полученный результат с оптимизируемым критерием в методе максимума правдоподобия при аддитивной помехе можно сделать вывод об их полной идентичности.

Приведем примеры оптимальных функций потерь и их производных.

1. Нормальная плотность распределения помех (плотность распределения Гаусса) при условии взаимной некоррелированности измерений

f (η) =	1	exp	−η2	/ 2σ2	(i)	= N (0,σ	η	(i)) .
	2π ση(i)			η

Функция потерь, согласно (3.4.49), будет иметь вид:

F *(ε) = ε2 / 2ση2 (i) + ln 2πση(i) ,

′	2	(3.4.50)
F * (ε) = ε / ση(i) .

Поскольку положение экстремума не зависит от постоянного слагаемого ln 2πση(i) , то можно записать следующий оптимизируемый критерий:

	N
J (c ) = ∑( y(i) − y(i))2 (1					ση(i))
	i=1
или в векторной форме:			т	D
	J (c ) = ( y − y)				( y − y) .
				η

Таким образом, при нормальном законе распределения использование оптимальной функции потерь эквивалентно применению метода наименьших квадратов.

2. Экспоненциальная плотность распределения помех (плотность распределения Лапласа) при условии взаимной некоррелированности измерений

f (η) = 2α1(i) exp[− η / α(i)] = L(0,α(i)) .

227

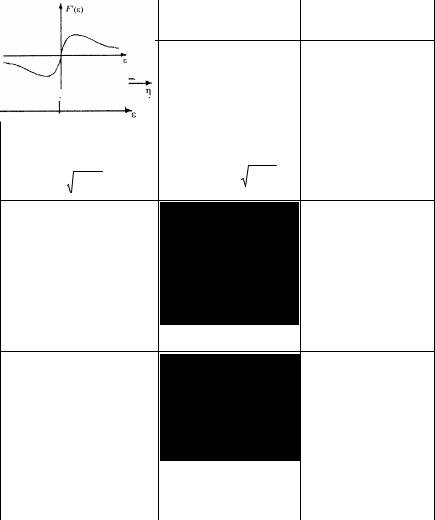
	Таблица 3.1
Оптимальные функции потерь и их производные
Плотность	Функция потерь F(ε) Производная функции
распределения f(η)	потерь F′(ε)

2	1		−η2 / 2ση2
N (0,ση) =	2	e			ε2 / 2ση2 + ln 2πση2		ε/ ση2
	2πση

	1	−		η
				s
L(0, s) =		e					ε		/ s + ln 2s	1/ s sign ε
	2s

c(0,s) =

1

1

2ε/(s2 + ε2 )

πs

η 2

1

+

ln(s

2

2

π

s

+ ε

) + ln

s

Для функции потерь получаем:

F * (ε) =

ε

/ α(i) + ln 2α(I) ,

′

F * (ε) = sign ε / α(i) . (3.4.51)

228

В данном случае получили модульную функцию потерь. Использование метода наименьших квадратов дает худшие асимптотические свойства оценок.

3. Дробная плотность распределения помех (плотность распределения Коши) при условии взаимной некоррелированности измерений

f (η) =	1		1			= C(0,α(i)) .
			1+ (η/ α(i))	2
	πα(i)

В этом случае имеем:

F * (ε) = ln(α(i)2 + ε2 ) + ln π / α(i) ,

′	2	+ ε	2	) .	(3.4.52)
F * (ε) = 2ε / (α(i)

Эти и некоторые другие виды функций потерь и их производные приведены в табл.3.1 [13].

3.4.6. Асимптотическая матрица ковариаций ошибок оценки при оптимальной функции потерь

Найдем, чему равна асимптотическая матрица ковариаций при

оптимально выбранной функции потерь, т.е.
F * (ε) = −ln f (η) η=ε .	(3.4.53)

Подставив выражение (3.4.53) для оптимальной функции потерь в формулу для АМКО (3.4.40), получим:

∞

′2

(η)dη

∫

f (η)F *

A−1

(c ,ση2 )=

V(F*, f ) =

−∞

2

∞

′

′

∫

f (η)F * (η)dη

−∞

∞

′

2

dη

∫ f (η)[(−ln f (η)) ]

(c ,ση2 )=

=

−∞

A−1

2

∞

f ′(η)(−ln f (η))′d

∫

η

−∞

229

	∞	′	2
	∫ f (η)[ f			dη
		(η) / f (η)]				(c ,ση2 ).
=	−∞				A−1
	∞

∫ f ′(η)[− f ′(η) / f (η)]dη

−∞

Приводя подобные члены, окончательно получаем:

V(F*, f ) = V( f ) =	A−1	(c ,ση2 )	.	(3.4.54)
	∞
	∫ [ f ′(η)]2 / f (η)dη

−∞

Выражение, стоящее в знаменателе (3.4.54), называется информацией Фишера и обозначается IF ( f (η)) , т.е.:

∞

IF ( f (η)) = ∫ [ f ′(η)]2 / f (η)dη.

(3.4.55)

−∞

Очевидно, справедливо следующее неравенство:

V(F, f ) ≥ V(F*, f ) ,

(3.4.56а)

где

F(η) – любая функция потерь,

F * (η) = −ln f (η) . Или, рас-

крывая V(F, f ) и V(F*, f ) , получим:

∞

− ∫ F′2 (η) f (η)dη

1

−∞

A−1 (c ,ση2 )≥

A−1 (c,ση2 ).(3.4.56б)

∞

2

∞

2

′

∫ f ′

(η) / f (η)dη

′

∫ F (η) f (η)dη

−∞

−∞

Важно отметить, что, если нормированная асимптотическая мат-

рица не зависит от параметра c и дисперсии шума ση2

(линейный

регрессионный объект), то неравенство (3.4.56б) можно упростить:

∞

F′2 (η) f (η)dη

∫

1

−∞

≥

.

(3.4.57)

∞

∞

f

′2

(η)

dη

∫

F′(η) f ′(η)dη

∫

−∞

f (η)

−∞

Таким образом,

знание плотности распределения помехи f (η)

позволяет определить оптимальную функцию потерь.

При этом

230