Загребаев Методы обработки статистической информации в задачах контроля 2008

fn (x1, ..., xn ; t1, ..., tn ) = fn (x1, ..., xn ; t1 + t0 , ..., tn + t0 ) ,										(2.1.10)
где t0 – любое число.
В частном случае при n =1 ,				n = 2 и при t0 = −t1 получим:
f	′(x, t ) = f ′(x, t				−t ) = f (x) ;					(2.1.11)
1		1	1	1		1			1
f2′(x1, x2 , t1, t2 ) = f2′(x1, x2 , 0, t2 −t1) =
= f ′(x, t		−t	) = f ′(x , x				, t	2	−t ).	(2.1.12)
1	1	1		2	1	2			1

Из определения математического ожидания и приведенных формул

(2.1.11) и (2.1.12) следует:

+∞	+∞
mx (t) = ∫	xf1(x, t)dx = ∫ xf1(x)dx = const ;	(2.1.13)
−∞	−∞

+∞

Dx (t) = ∫ {x(t) −mx(t)}2 f1(x,

−∞

+∞+∞

K(t1, t2) = ∫ ∫ (x1 −mx) (x2 −mx)

−∞−∞

+∞

t)dx = ∫ (x −mx)2 f1(x)dx =const ; (2.1.14)

−∞

f2(x1, x2, t2 −t1, t)dx1dx2 =K(t2 −t1) . (2.1.15)

Таким образом, если случайная функция стационарна, то ее математическое ожидание и дисперсия постоянны, а корреляционная функция зависит только от разности аргументов. Но это условие является необходимым условием, так как для n > 2 условие (2.1.10) может нарушаться. Поэтому говорят, что при выполнении условий (2.1.14) – (2.1.15) случайная функция стационарна в широком смысле.

Нормальные и ненормальные случайные функции

Случайные функции различают также в зависимости от законов распределения ординат случайных функций. Если многомерные законы распределения являются нормальными, то такие случайные функции называются нормальными. Это класс случайных функций наиболее часто встречается. Остальные функции называются ненормальными. Если нормальная функция стационарна в широком смысле, то она стационарна и в узком смысле.

111

Свойства корреляционных функций.

1.K (t1, t2 ) = K (t2 , t1 ) .

2.| K (t1, t2 ) | ≤ K(t1, t1 ) K (t2 , t2 ) .

b b

3. ∫∫η(t1 )η(t2 )K(t1, t2 )dt1dt2 ≥ 0 , где η(t) – произвольная неслу-

a a

чайная функция; (a, b) – произвольный интервал интегрирования.

Если случайная функция стационарна, то эти свойства записываются следующим образом.

1.K (τ) = K(−τ) .

2.K (0) = D ≥ K (τ) .

b b

3. ∫∫η(t1 )η(t2 )K (t2 −t1)dt1dt2 ≥ 0 , где τ = t2 −t1 .

a a

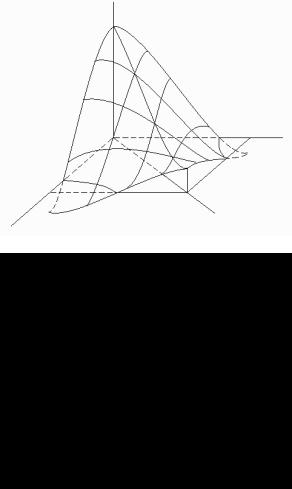
На рис. 2.3 показан вид корреляционной функции от двух аргументов.

K(t1, t2 )

t1

t2

t1 = t2

Рис. 2.3. Пример корреляционной функции двух аргументов

Наиболее часто в качестве стационарных случайных функций рассматриваются следующие:

K (τ) = σ2 exp(−α| τ|) ; K (τ) = σ2 exp(−ατ2 ) ;

112

K(τ) = σ2 exp(−α| τ|) cosβτ;

K(τ) = σ2 exp(−ατ2 ) cosβτ .

Непрерывность, дифференцируемость и интегрируемость случайных функций

Непрерывность. Случайная функция X (t) называется непрерывной в точке t, если при любом ε > 0 найдется такое δ > 0 , что при | t′ −t |< δ выполняется неравенство M[| X (t′) − X (t) |2 ] < ε .

Можно доказать, что если X (t) – непрерывная функция, то mx (t) и K(t, t′) – также непрерывные функции. Справедливо и обратное

утверждение. Отметим, что непрерывная случайная функция может иметь разрывные реализации. Непрерывность случайной функции – болееобщий типнепрерывности, чем для неслучайнойфункции.

Дифференцируемость. Случайная функция										X (t) дифференци-
руема, если существует такая случайная функция Y (t) , что
				X (t +	t) − X (t)				2
lim M						−Y (t)				= 0 .
					t
t→0
Случайная функция				Y (t)	называется		производной случайной

функции и обозначается dXdt =Y или X ′(t) .

Можно доказать, что если случайная функция дифференцируема, т.е. Y = dXdt , то

my =		dmx		;		(2.1.16)
		dt
				′
Ky =	∂Kx (t, t )				.	(2.1.17)
		′
		∂t ∂t

Верно и обратное утверждение.

Интегрируемость. Случайную функцию X (t) называют интегрируемой на области T с весом g(s, t) , если существует такая случайная функция Y (s) , что

113

			∑g(s, tk )X (tk ) tk −Y (t)		2
lim	M					= 0
max tk →0			k

независимо от выбора точек tk соответствующих участков			tk , на
которые разбита область T.
Случайная функция Y (s) называется интегралом.
Можно доказать, что если X (t) – интегрируемая функция, то
my (s) = ∫ g(s, t)mx (t)dt ;			(2.1.18)
T
K y (s, s′) = ∫∫g(s, t)g		Kx (t, t′)dtdt′ .	(2.1.19)
	(s, t)
T

Справедливо и обратное утверждение.

Из приведенных выше определений дифференцируемости и интегрируемости случайных функций следует, что эти операции можно менять местами с операцией нахождения математического ожидания.

2.2. Операции над случайными функциями и их статистическими характеристиками

Действие линейного оператора на случайную функцию

Пусть X (t) случайная функция с математическим ожиданием

					′	. Тогда,		если на эту
mx (t) и корреляционной функцией Kx (t, t )
функцию действует линейный оператор					ˆ
					L , то числовые характери-
	ˆ	есть:
стики функции Y = LX
		ˆ		ˆ		ˆ	;	(2.2.1)
M[Y (t)] = MLt X (t) = Lt M[ X (t)] = Lt mx (t)
		′	ˆ	ˆ	′			(2.2.2)
		K y (t, t ) = Lt Lt′Kx			(t, t ) .
ˆ	ˆ	действуют, соответственно, на переменные t
Операторы Lt	и Lt′

и t′ , а оператор математического ожидания M производит усреднение ординат случайной функции при фиксированных значениях t и t′ по всему множеству возможных значений случайных вели-

114

чин X (t) и X (t′) соответственно, поэтому порядок этих операций

можно менять местами.

Белый шум. Белым шумом называется случайная функция со следующими свойствами:

mx (t) ≡ 0 ; Kx (t, t′) = G(t)δ(t −t′) ,

где δ(t −t′) – дельта-функция Дирака; G(t) – интенсивность белого

шума.

Если функция X (t) представляет собой белый шум, то для функции Y (s) = ∫ g(s, t)X (t)dt ее корреляционная функция имеет вид

T

T
K y (s, s′) = ∫	g(s′, t)	g(s, t)G(t)dt .	(2.2.3)
0

Физический смысл понятия «белый шум» будет показан в разделе, посвященным стационарным случайным функциям.

Каноническое разложение случайной функции

Каноническим разложением случайной функции называется функция вида

m
X (t) = mx (t) + ∑Vi ϕi (t) ,	(2.2.4)

i=1

где ϕi (t) – неслучайные функции; Vi – случайные некоррелированные между собой величины с нулевыми математическими ожиданиями, т.е. M[Vi ] = 0 и M[ViVj ] = 0 при i ≠ j .

Иногда используют так называемое интегральное каноническое представление случайной функции:

X (t) = mx (t) + ∫V (λ) ϕ(t, λ)dλ ,	(2.2.5)
λ

где V (λ) – белый шум параметра λ; ϕ(t, λ) – неслучайная функция.

Идея метода состоит в том, что применение линейного оператора к случайной функции сводится к его действию на известную неслучайную функцию. Это обстоятельство существенно упрощает нахождение статистических характеристик линейных систем. Дей-

115

ствительно, пусть требуется найти математическое ожидание и

корреляционную функцию результата				действия оператора	ˆ	на
					L
функцию X (t) :
ˆ		ˆ	m
Y = LX (t) = L{mx (t) + ∑Vi ϕi (t)} =
			i=1
ˆ	m		ˆ	m
				(t) + ∑Vi ψi (t);	(2.2.6)
= Lmx (t)	+ ∑Vi Lϕi (t) = my
	i=1			i=1

	ˆ
my (t) = Lmx (t) ;
m		m
K y (t, t′) = M ∑Vi ψi (t)		∑Vj ψ j (t′)
i=1	j=1

m

= ∑Di ψi (t′)ψi (t).

i=1

(2.2.7)

⎟⎥=

(2.2.8)

Если в выражении (2.2.7) положить t = t′, получим простое выражение для дисперсии функции:

m
Dy (t) = ∑Di ψi2 (t) .	(2.2.9)

i=1

Вдальнейшем будем рассматривать центрированную случайную функцию X (t) = X (t) − mx (t) .

Способ получения приближенного канонического разложения случайной функции

На практике часто удается приближенно представить случайную функцию в виде линейной комбинации известных функций со случайными коэффициентами:

m
X (t) = ∑Aiϕi (t) ,	(2.2.10)

i=1

где ϕi (t) – не случайные функции; Ai –− случайные коэффициен-

ты, причем в общем случае коррелированные. Требуется привести случайную функцию X (t) к каноническому виду.

116

Математическое ожидание случайной функции X (t) есть

m

mX (t) = ∑mAi ϕi (t) .

i=1

Перейдем от случайных величин Ai к таким случайным величинам Vi , чтобы

при

i ≠ j

и

M [Vi ]= 0 .

M Vi

Vj = 0

Сделать это можно, например, следующим образом. Положим

A1 − mA =V1;

1

− mA

= a21V1 +V ;

A2

2

− mA

= a31V1 + a32V2 +V3;

(2.2.11)

A3

3

...;

A

− m

Am

= a

V + a

V +... + a

V

+V .

m

m1 1

m2 2

m,m−1 m−1

m

Определим

введенные

нами

коэффициенты

aij

так, чтобы

= 0

при i ≠

j . Очевидно, что D[A1]= D[V1].

M Vi Vj

Умножим почленно второе уравнение системы (2.2.11) на первое и возьмем математическое ожидание:

М (A2	− mA	)(A1	− mA	)	= М (a21V1	+V2 )V1	;
	2		1

K21 = a21D[V1 ]+ M [V2V1 ].

Полагая M [V1 V2 ]= 0 , получим

a	21	=	K21		=	K21		.
			D[V	]		D[A	]
			1			1

Определим теперь дисперсию (второе уравнение)

D A2 − M A2 = D[a21V1 +V2 ];

K22 = a21 2 D[V1 ]+ D[V2 ],

иотсюда определим D[V2 ].

117

Далее умножаем почленно третье уравнение системы (2.2.11) на первое и второе, выполняем операцию математического ожидания

и определяем a31 и a32 , исходя из условия, чтобы M [V1 V3 ]= 0 и

M[V2 V3 ]= 0 , и т.д.

Врезультате получаем выражения для A1, ..., Am в виде линей-

ных комбинаций некоррелированных случайных величин V1, ..., Vm :

			m−1
A1	= mA +V1; ...;	Am = mA	+ ∑ amiVi +Vm .	(2.2.12)
	1	m
			i=1

Подставим эти значения в исходное выражение (2.2.10), и после перегруппировки получим:

m
Х mХ (t) + ∑Viψi (t) ,	(2.2.13)

i=1

m

где ψi (t) = ϕi (t) + ∑ akiϕk (t) , i =1, ..., k −1 .

k =i+1

Таким образом, получено приближенное представление исходной функции как функции канонического разложения. При этом использовалась информация о статистических свойствах функции в форме ковариационных моментов амплитуд исходного представления. Новые неслучайные функции разложения ψi (t) , которые но-

сят название координатных функций, являются линейными комбинациями исходного набора {ϕi (t)} .

2.3. Спектральное разложение стационарных случайных функций

Характеристики стационарной случайной функции

Рассмотрим случайную функцию X(t) – стационарную в широком смысле. По определению стационарности в широком смысле X(t) имеет постоянное математическое ожидание и корреляционную функцию, зависящую только от разности аргументов t и t′, т.е.

K (t, t ') = K (τ) , где τ = t −t′ .

118

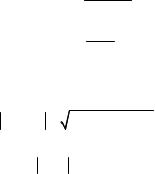
В этом случае дисперсия стационарной случайной функции

D[X (t)]= K(t, t) = K (0) .

Нормированная корреляционная функция стационарной случайной функции есть

r(τ) =	K (τ)	.	(2.3.1)
	K (0)

На основании свойства симметрии корреляционной функции можно записать:

K (t′−t) = K(t −t′)

или

K (−τ) = K(τ) .

Для действительной случайной функции K (−τ) = K(τ) . Второе свойство корреляционной функции:

K (t, t′) ≤ K(t′, t)K (t, t′)

записывается в виде

K (τ) ≤ K (0) .

Наконец, корреляционная функция для производной от стационарной случайной функции Y = dX 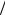dt

′

∂

2

′

∂

2

K(τ)

∂

2

K (τ) ∂τ ∂τ

∂

2

K (τ)

K(t, t )

=

=

=

.

KY (t, t ) =

∂t ∂t′

∂t ∂t′

∂τ2 ∂t ∂t′

∂τ2

mX = const, mY = 0 = const .

Таким образом, производная случайной функции Y = dX 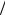dt яв-

ляется также стационарной случайной функцией.

Пример 2.1. Случайная функция X (t) задана каноническим разложением:

X (t) = t +V1 cos ωt +V2 sin ωt ,

где M [V1 V2 ]= 0 , M [V1 ]= M [V2 ]= 0 , D1 = D2 = 2 .

Определить, является ли стационарной случайная функция

X (t) .

119

Решение:

mx (t) = t ;

K (t, t′) = 2(cos ωt cos ωt′+ sin ωt sin ωt′) = 2cos ω(t −t′).

Так как mx (t) ≠ const , то функция X (t) является нестационарной, однако ее легко можно привести к стационарной путем цен-

трирования X = X (t) −t . Эта функция уже будет стационарной.

Спектральное разложение случайной функции

Спектральным разложением случайной функции интервале от 0 до T называется ее представление в виде

∞
X (t) = ∑ (Wk cos ωkt +Vk sin ωk t),	(2.3.2)

k=0

где ωk = kTπ , Wk и Vk – некоррелированные случайные величины с

одинаковыми дисперсиями D[Wk ]= D[Vk ]= Dk .

Легко показать, что корреляционная функция при этом имеет вид:

	∞						∞
	K (t, t′) = ∑ (Dk cos ωk t′cos ωk t + Dk sin ωkt′sin ωkt )= ∑ Dk cos ωk τ ,
	k=0						k =0
	где коэффициенты Dk задаются формулами:
					1	T
			D0 =			∫ K (τ)dτ;
					2T
						−T
	Dk =	1	T	K (τ) cos ωk τdτ			при k ≠ 0 .
			∫
		T
			−T
	Дисперсия случайной функции имеет вид:
	D[X (t)]		∞	(cos2 ωkt + sin2			∞
		= ∑					ωk t)Dk = ∑ Dk .
			k =0				k =0

120