Загребаев Методы обработки статистической информации в задачах контроля 2008

мые по формулам (2.5.7), представляют собой каноническое разложение случайной функции ϕ(r ).

Заметим, что каждая из построенных функций представляет собой линейную комбинацию выбранных «базисных» функций

{ Ψk (r )}, коэффициенты которой (элементы матрицы Λ ) опреде-

ляются вероятностными характеристиками вектора A . Поскольку последние на практике заменяются их статистическими оценками, можно вести речь лишь о построении приближенного канонического разложения по описанной методике.

Таким образом, задача построения приближенного канонического разложения случайной функции ϕ(r ) по результатам статистического эксперимента разбивается на следующие этапы:

1)выбирается набор координатных функций { Ψk (r )};

2)для M реализаций случайной функции ϕ(r ) методом наи-

меньших квадратов производится аппроксимация показаний датчиков выбранным набором функций:

ϕˆ (r,t j )= AТ (t j )Ψ(r ), j =1, M ;

3) по набранному таким образом архиву реализаций случайного

вектора A находятся оценки его вероятностных характеристик – математического ожидания и корреляционной матрицы;

4)по рекуррентным соотношениям (2.5.5) рассчитываются элементы треугольной матрицы Λ ;

5)в соответствии с выражениями (2.5.7) строятся функции при-

ближенного канонического разложения { Ψk (r )}.

Теоретическое обоснование связи собственных функций невозмущенного реактора с оптимальными координатными функциями канонического разложения

Рассмотрим реактор в одногрупповом диффузионном приближении с нулевыми граничными условиями, в котором случайным образом флюктуируют свойства среды:

Δϕ(r ) + (æ02 (r ) + ε(r )+ Θ)ϕ(r ) = 0 ,

(2.5.8)

141

где ϕ(r ) – плотность потока нейтронов, нейтр./(м2 c); ε(r ) – слу-

чайное возмущение в свойствах среды, 1/м2; Θ – параметр, обеспечивающий критичность реактора, 1/м2.

В дальнейшем для краткости функцию координат æ02 (r ) будем

называть материальным параметром.

Представим плотность потока нейтронов и материальный параметр в виде суммы детерминированной и случайной составляющих:

ϕ(r ) = ϕ0 (r ) + δϕ(r ) ;

æ2 (r )= æ02 (r )+ ε(r ),

(2.5.9)

где δϕ(r ) , ε(r ) – случайные составляющие; ϕ0 (r ) , æ02(r) – детер-

минированные функции координат.

Подставляя выражения (2.5.9) в уравнение (2.5.8) и пренебрегая членами второго порядка малости, т.е. произведениями δϕ(r ) ε(r ) и Θ δϕ(r ), получим:

Δϕ0 (r )+ æ02 (r )ϕ0 (r )+ Δδϕ(r )+ æ02 (r )δϕ(r )+
+(ε(r )+ Θ)ϕ0 (r ) = 0 .	(2.5.10)

Применяя к этому уравнению линейную операцию нахождения математического ожидания, будем иметь:

Δϕ		0	(r )+ æ2	(r )ϕ	0	(r )	+ M δϕ(r ) +
			0
+æ2	(r )M δϕ(r ) + M ε(r )+ Θ ϕ							0	(r ) = 0 . (2.5.11)
0

Предполагая, что математические ожидания возмущений имеют нулевые значения, т.е.

M ε(r )	= M [Θ]= M δϕ(r ) = 0		,	(2.5.12)

получим, что M [ϕ(r )]= ϕ0 (r ) , и математическое ожидание плотности потока нейтронов подчиняется уравнению

Δϕ0 (r )+ æ02 (r )ϕ0 (r ) = 0 ,	(2.5.13)
142

а конкретная реализация случайного отклонения плотности потока нейтронов от математического ожидания – уравнению

Δδϕ(r )+ æ02 (r )δϕ(r )+ (ε(r )+ Θ)ϕ0 (r ) = 0 .

(2.5.14)

Умножая уравнение (3.6) на δϕ(r ) , а уравнение (2.5.14) – на ϕ0 (r ) , интегрируя их по объему реактора с учетом граничных ус-

ловий, получим выражение для конкретной реализации параметра

Θ:

∫ε(r )ϕ02 (r )dr

Θ = −V . (2.5.15)

∫ϕ02 (r )dr

V

Пусть G(r , r0 ) – функция Грина невозмущенного реактора с нулевыми условиями на экстраполированной границе:

G (r , r	)+ æ2	(r )G (r , r	)= δ(r, r	).	(2.5.16)
0	0	0	0

Выразим решение уравнения (2.5.14) через функцию Грина:

δϕ(r )= −	∫	G (r , r	) ε(r )+ Θ		ϕ	0	(r )dr .	(2.5.17)
		0					0

V

Тогда корреляционная функция плотности потока нейтронов будет иметь вид:

K

ϕ (

r , r′

)

(

r

)

(

)

= M δϕ

δϕ

r′ =

′

(r0 )ϕ0

(r1 )dr0dr1 .

= ∫ ∫G(r, r0 ) G(r , r1 ) M (ε(r0 )+Θ)(ε(r1 )+Θ) ϕ0

V V

(2.5.18)

Явный вид выражения M [(ε(r0 ) + Θ)(ε(r0 ) + Θ)] получим, подставив вместо Θ выражение (2.5.15):

∫

ε(s )

ϕ2

(s )ds

∫

ε(p)

ϕ2

(p)dp

ε(r

)−

0

ε(r )−

0

V

V

M

=

0

∫ϕ02 (s )ds

1

∫ϕ02 (p)dp

V

V

143

1

= M ε(r

)ε(r )

−

ϕ2

(s ) M ε(s )ε(r ) ds +

0

1

∫

ϕ2 (r )dr ∫

0

1

0

V

V

+

ϕ2

(p) M ε(p)ε(r

+

∫

) dp

0

0

V

∫ ∫

ϕ2

(p)ϕ2

(s )M ε(p)ε(s ) dpds

0

0

+

V V

.

(2.5.19)

ϕ2

2

∫

(r )dr

0

V

Таким образом, корреляционная функция плотности потока нейтронов есть

Kϕ (r, r′) = ∫ ∫G (r, r0 )G (r′, r1 )ϕ0 (r0 )ϕ0 (r1 ) {Kε (r0 , r1 )−

V V

1

−

∫

ϕ2

(s )K

ε

(s, r )ds +

∫

ϕ2

(p)K

ε

(p, r

)dp

+

2

0

1

0

0

∫ϕ0

(r )dr V

V

V

∫ ∫ϕ02 (p)ϕ02 (s )Kε (p, s )dpds

+

V V

dr dr .

(2.5.20)

2

0

1

∫ϕ02

(r )dr

V

Выражение (2.5.20) существенно упрощается, если учесть, что оператор L = + æ02 (r ) является самосопряженным. Тогда выполняется условие ортогональности:

∫G (r , r1 )ϕ0 (r1 )dr1 = 0	(2.5.21)
V

и выражение для корреляционной функции принимает вид:

Kϕ (r, r′) = ∫∫G(r, r0 ) G(r′, r1)ϕ0 (r0 )ϕ0 (r1) Kε (r0, r1)dr0dr1 . (2.5.22)

V V

144

Известно, что функция Грина для самосопряженного оператора имеет вид:

	∞	1		ϕk (r ) ϕk (ξ)
	G (r, ξ)= ∑				,	(2.5.23)
		λ′k		∫ϕk2 (r )dr
	k =1

V

где ϕk (r ) – собственные функции краевой задачи:

Δϕk (r )+ æ02ϕk2 (r )= λ′k ϕk (r );			(2.5.24)
ϕk (r )		= 0.
	S

где S – экстраполированная граница реактора.

Таким образом, корреляционная функция реактора выражается через его собственные функции.

С другой стороны, координатные функции оптимального канонического разложения являются собственными функциями интегрального уравнения Фредгольма второго рода, где ядром является корреляционная функция:

λk Ψ(r )= ∫ K (r,ξ) Ψ(ξ)dξ .	(2.5.25)
V

Подставляя выражение (2.5.23) в формулу (2.5.22), а затем в (2.5.25), получим связь между собственными функциями реактора и координатными функциями оптимального канонического разложения:

		∞ ∞	1
	λk Ψ (r ) = ∫ ∫ ∫ ∑ ∑				×
		V V V k =1 m =1	λ′k λ′m
×	ϕk (r )ϕk (r0 )ϕm (r1 )ϕm (ξ)ϕ0 (r0 )ϕ0 (r1 )Kε (r0			, r1 ) Ψ(ξ)		dr dξdr.
	∫ϕk2 ( p)dp ∫ϕm2 (p)dp					1
	V	V

(2.5.26)

Как видно из этого выражения, зависимость между собственными функциями невозмущенной задачи и координатными функциями оптимального канонического разложения определяется корреляционной функцией флюктуаций в свойствах среды Kε (r0 , r1) .

Если флуктуации в свойствах среды представляют собой белый

145

шум, т.е. Kε (r0 , r1) = Dεδ(r0 , r1) , то корреляционная функция будет иметь вид:

Kϕ (r, r′)= Dε ∫G(r, r0 )G(r0, r′)ϕ20 (r0 )dr0 = Dε Gα (r, r′). (2.5.27)

V

Поставим следующую задачу на собственные функции и собственные значения для интегрального уравнения:

λΨ(r )= ∫Ψ(ξ)G (r, ξ)ϕ02 (ξ)dξ .	(2.5.28)
V

Умножив левую и правую части этого уравнения на функцию G(r, r′) ϕ02 (r ) и проинтегрировав по переменной r , получим:

λ∫Ψ(r )ϕ02 (r )G (r , r′)dr = ∫ ∫G (r, r′)ϕ02 (r )G (r , ξ)Ψ(ξ)ϕ02 (ξ)drdξ =

V	V V
	= ∫ ∫G (r , r′)G (r , ξ)ϕ02 (r )dr ϕ02 (ξ)Ψ(ξ)dξ , (2.5.29)
	V V
	Gα(ξ, r )

откуда следует, что собственные функции задачи (2.5.28) являются собственными функциями следующей задачи:

λ2 Ψ(r′)= ∫Gα (ξ, r′)ϕ02 (ξ)Ψ(ξ)dξ ,	(2.5.30)
V

т.е. оптимальными координатными функциями канонического разложения, так как Gα (ξ, r′) в соответствии с (2.5.27) является кор-

реляционной функцией.

С другой стороны, интегральное уравнение (2.5.28) эквивалентно следующей краевой задаче:

ΔΨ(r )+ æ2 (r )Ψ(r )= λϕ2 (r )Ψ(r );

0 0 (2.5.31)

Ψ(r )S = 0.

Таким образом, если возмущение представляет собой белый шум, то корреляционная функция плотности потока нейтронов является повторной функцией Грина невозмущенной задачи, а опти-

146

мальные координатные функции канонического разложения – соб-

ственными функциями оператора	L =	1		L .
	1	ϕ2	(r )
		0

Нетрудно показать также, что в этом случае взаимная корреляционная функция плотности потока нейтронов и возмущений среды имеет вид

Kε, δϕ = Dεϕ0 (r0 ) G(r , r0 ) .

Каноническое представление плотности потока нейтронов в реакторе в форме бесконечной плоской пластины

Рассмотрение реактора в форме бесконечной плоской пластины может позволить не только более наглядно представить полученные выше результаты, но имеет и практическое приложение, например, для анализа высотных полей. В этом случае уравнение (2.5.8) примет вид

	d 2ϕ(z)		+ æ02 (z)ϕ(z)+ ε(r )ϕ(z)+ Θ ϕ(z)= 0;
						(2.5.32)
		dz2
	ϕ(0)= ϕ(H ) = 0,
	где H – экстраполированный размер реактора.			z
	Для удобства введем замену переменных x =				, тогда x [0,1].
				H

Уравнение для собственных функций невозмущенного реактора будет иметь вид:

	d 2ϕ(x)	+ æ02	(x)H 2ϕ(x)= μH 2ϕ(x),	(2.5.33)
	dx2

а уравнение для оптимальных координатных функций канонического разложения в соответствии с выражением (2.5.31) – следующий вид:

d 2Ψ(x)	+ æ2 H 2	Ψ(x)= λϕ2	(x)Ψ(x)H 2 .	(2.5.34)
dx2	0	0

При этом предполагается, что возмущения представляют собой белый шум.

147

Для сравнения оптимальных координатных и собственных функций невозмущенного реактора рассмотрим реактор с зоной «плато». Распределение материального параметра и плотности потока нейтронов в этом случае показаны на рис. 2.17.

250

200

150

100

50

0

0

0,2

0,4

0,6

0,8

1

x, отн.ед.

а

1,5
1
0,5
0
0	0,2	0,4	0,6	0,8	1
			б	x, отн.ед.

Рис. 2.17. Распределение материального параметра (а) и плотности потока нейтронов (б) в трехзонном реакторе

Активная зона реактора представляет собой компоновку из трех зон. В периферийных зонах значения материального параметра

одинаковы и равны величине π 2 , где δ – ширина периферийной

2δ

зоны. Степень уплощения поля нейтронов будем характеризовать величиной параметра p = 1 −12δ =1 − 2δ. При p = 0 реактор пред-

ставляет собой пластину с однородными свойствами, при p =1 –

бесконечный реактор. Математическое ожидание распределения материального параметра и плотности потока нейтронов в таком реакторе имеют следующие зависимости:

				π	2							1 − p
							, 0		≤ x		≤			;
		1											2
				− p
				1 − p						1 + p
æ02 (x) H 2							< x							(2.5.35)
	= 0,								<				;
				2							2
				π	2				+ p
							,	1			≤ x ≤1;
		1							2
				− p

148

πx

≤ x ≤

1 − p

sin

, 0

;

2

1

− p

1− p

1+ p

ϕ0

(x)=

1,

< x <

;

(2.5.36)

2

2

π(2x − p −1)

1 + p

≤ x

≤1.

cos

,

2 1− p

2

)

(

Введем обозначения:

æ02 H 2 = æ2 ,

λ H 2 = λ ,

μ H 2 = μ . Тогда

уравнения для собственных функций и функций оптимального канонического разложения, соответственно, примут вид:

d 2ϕ(x)

+ æ2

(x) ϕ(x)= μˆ ϕ(x),

dx2

1

d2Ψ(x)

2

ˆ

+æ

(x)Ψ(x)

= λ Ψ(x);

ϕ2

dx2

(x)

0

Ψ(0)= Ψ(1)= 0.

(2.5.37)

(2.5.38)

Решение задач (2.5.37) и (2.5.38) будем искать методом Галеркина. Для этого представим функции ϕ(x) и Ψ(x) в виде суперпо-

зиций по собственным функциям однородного плоского реактора:

K
Ψ(x)= ∑Ai sin (πi x);	(2.5.39)
i=1
K
ϕ(x)= ∑Bi sin (πi x).	(2.5.40)

i=1

Подставляя эти выражения, соответственно, в уравнения (2.5.37) и (2.5.38), умножая обе части уравнения на sin(πjx) и интегрируя

по объему, получим задачи линейной алгебры на собственные значения и собственные векторы:

M B = μ B ;	(2.5.41)
R A = λ A,	(2.5.42)

где R и M – квадратные матрицы размера (k ×k ) .

149

Оптимальные координатные функции канонического разложе-

10

ния находятся при этом из соотношения ψi (x) = ∑ Aki sin(π i x) , а

k =1

10

собственные функции – из соотношения ϕi (x) = ∑ Bki sin(π i x) .

k=1

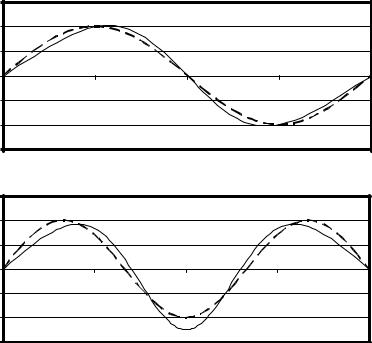
На рис. 2.18 показаны первые пять собственных функций однородного реактора и первые пять функций оптимального канонического разложения.

1,5
1
0,5
0			х
-0,5	0	0,5		1
-1
-1,5
		а) k = 1

1,5
1
0,5
0			х
-0,5	0	0,5		1
-1
-1,5		б) k = 2

Рис. 2.18. Собственные функции ψk (сплошные линии) однородного реактора и функции оптимального канонического разложения ξk (пунктир), см. также с. 151

150