Загребаев Методы обработки статистической информации в задачах контроля 2008

замедления, где ξ ∑S называется замедляющей способностью, а ∑S и ∑a – макроскопическими сечениями рассеяния и поглоще-

ния соответственно. Чем больше K, тем лучше замедлитель. С точки зрения нейтронно-физических процессов наилучшим замедлителем является тяжелая вода, затем следует графит и, наконец, обычная вода.

Таблица 1.3

Константы, характеризующие замедление нейтронов

Нуклид	А	ξ	N
Водород	1	1,000	18
Дейтерий	2	0,725	25
Углерод	12	0,158	114
Кислород	16	0,120	150
Уран	238	0,0084	2170

Рассмотрим теперь, как формируется спектр нейтронов (т.е. распределение замедляющихся нейтронов по энергиям) при замедлении на водороде (это самый простой случай).

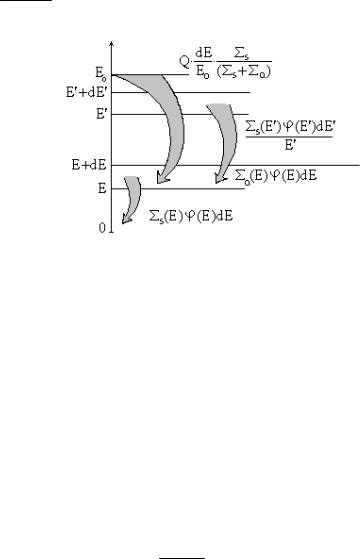
Пусть в единице объема в единицу времени рождается Q0 нейтронов с энергией E0 . Рассмотрим баланс нейтронов в интервале d E около энергии E ( E < E0 ) (рис. 1.29).

Число нейтронов, прибывающих в единицу времени в этот интервал, складывается из двух составляющих:

прибыль за счет однократного рассеяния нейтронов источника при энергии E0 ;

прибыль за счет рассеяния нейтронов в интервалах типа d E′, лежащих выше энергии E, но ниже E0 (т.е. E < E′ < E0 ).

Если Q0 – число нейтронов, испускаемых источником при энергии E0 , то ясно, что раньше или позже они испытают соударения с

ядрами среды (так как по условию среда бесконечна, следовательно, утечки нейтронов за ее пределы нет). Однако не каждое соударение приводит к реакции рассеяния. При наличии поглощения ве-

101

роятность нейтрону испытать именно рассеяние равна отношению

∑S . ∑S +∑a

Рис. 1.29. Энергетический баланс нейтронов

Следовательно, число нейтронов источника, испытавших рассеяние в результате первого столкновения, есть величина

		Q0 ∑S (E0 )
					.
∑	S	(E	) + ∑	(E )
		0	a	0

Обозначим ∑(E) = ∑S (E) + ∑a (E) .

Вероятность того, что в результате первого рассеяния нейтроны

	попадут в интервал энергий d E	около E, есть	d E	, так как при
			E
			0

рассеянии на водороде (A = 1) нейтроны с равной вероятностью приобретают энергию в пределах ступеньки замедления E0 ÷0 .

Таким образом, за счет однократного рассеяния нейтронов источника в интервал d E около E каждую секунду будет попадать чис-

ло нейтронов, равное

Q0 d E ∑S (E0 ) . E0 ∑(E0 )

102

Из интервала d E′ около E′ за счет рассеяния ежесекундно уходит ∑S (E′) ϕ(E′)d E′ нейтронов. Поскольку в результате рассеяния нейтроны будут иметь энергию в интервале E′÷0 с равной

вероятностью, то вероятность попасть в интервал d E будет dEE′ .

Значит, в результате многократного рассеяния нейтронов выше энергии E′ в интервал попадет d E число нейтронов, равное

	E0 ∑S (E′) ϕ(E′)									′
	∫			E′			d E d E .
	E
				F(E) =[∑S (E) + ∑a (E)] ϕ(E) , то это
Если ввести обозначение
выражение можно привести к виду:
E0	∑		′	′		d E			′
∫		S	(E ) F(E )							d E .
				′			E	′
E			∑(E )

Таким образом, общая прибыль нейтронов в интервал d E около E составляет величину

E0

∑

′

′

d E

′

Q

∑

(E )

S

(E ) F(E )

S

∫

′

E

′

d E +

0

0

.

E

∑(E )

E0

∑(E0 )

Убыль нейтронов из интервала

d E около E осуществляется за

счет поглощения ∑a (E) ϕ(E)d E и рассеяния ∑S (E) ϕ(E)d E . Поскольку рассматривается равновесный процесс замедления, то скорость убыли должна равняться скорости прибыли:

E0

∑

′

′

d E

′

Q

∑

(E )

S

(E ) F(E )

S

F(E) = ∫

′

+

0

0

. (1.4.12)

′

E0

E

∑(E )

E

∑(E0 )

Уравнение (1.4.12) носит название уравнения замедления. Его решение легко получить аналитически, если продифференцировать по E левую и правую части:

	d F	= −	∑S (E) F(E)	;	d F	= −	∑S (E)d E	;
	d E				F
			∑(E) E				∑(E) E

103

E0

′

d E

′

F(E) = F(E0 ) exp

∫

∑S (E )

.

E

∑(E′)

E′

Из выражения (1.4.12) получим

F(E ) =

Q0

∑S (E0 ) .

0

E0

∑(E0 )

Если учесть, что

∑S

=1 −

∑a

в показателе экспоненты, то

∑

∑

E0

∑

′

d E

′

E0

∑

d E

′

E0

d E

′

exp

∫

S

(E )

= exp −

∫

a

exp ∫

=

′

E

′

E

′

E

′

E

∑(E )

E

∑

E

E0

∑a

d E′

E0

= exp

− ∫

.

E

∑

E′

E

Окончательно получим:

Q0

E0

d E′

F(E) =

∑S (E0 ) exp − ∫

∑a

.

(1.4.13)

E

∑(E0 )

E

∑

E′

Если поглощение мало ( ∑a << ∑S ), то выражение (1.4.13) принимает вид

F(E) = QE0 .

Таким образом, энергетическое распределение нейтронов при замедлении на водороде имеет вид:

без поглощения –

	ϕ(E) =			Q0			(спектр Ферми);
				∑S E
	с поглощением –
			Q0					E0	′		′
	ϕ(E) =					exp − ∫			∑a (E )	d E	.
		∑S E
								E	∑(E′)	E′

104

Из сравнения этих двух формул понятно, что сомножитель

	E0	′	d E	′
exp − ∫		∑a (E )		имеет смысл вероятности избежать погло-
	E	∑(E′)	E′

щения при замедлении.

Если замедление происходит на произвольных ядрах среды, то можно показать, что спектр нейтронов описывается выражением

	Q		E0	∑	a		d E
ϕ(E) =	0	exp	− ∫					.
	ξ∑S E
			E	∑S +∑a			ξ E

Поскольку в области замедления сечения захвата малы, за исключением резонансного поглощения на ядрах топлива, то величина

	E0	∑	a		d E
p = exp − ∫
	E	∑S +∑a			ξ E

носит название вероятности избежать резонансного захвата. Приведенные выше энергетические спектры связаны с плот-

ностью распределения вероятности следующим образом:

f (E) =		ϕ(E)	,
	E	0
	∫ ϕ(E)dE

Ec

где Ec – уровень энергии, разграничивающий область замедления

и область тепловых энергий.

Используя функцию f (E) , находят средние значения взаимодействия в области замедления:

	E0
	∫	σ(E)ϕ(E)dE
σ =	Ec		.	(1.4.14)
		E
		0
		∫ ϕ(E)dE

Ec

Спектр тепловых нейтронов. В тепловой области энергий спектр нейтронов описывается распределением Максвелла вида

105

	ϕ( E ) =	2 π E		−	E
			ex p				,
		( πkTn )3 / 2
					kTn

где k – постоянная Больцмана; Tn – температура нейтронного газа,

зависящая от температуры замедлителя и его поглощающих и замедляющих свойств. Тогда

		Σ	a
Tn =T 1	+1,5			,
		ξΣs

где T – температура среды.

Средние сечения в тепловой области находятся по следующей формуле:

∞

∫σ(E)ϕ(E)dE

σ =	0		.
		∞
		∫ϕ(E)dE
		0

Список литературы к главе 1

1.Айвазян С.А. и др. Прикладная статистика: Основы моделирования

ипервичная обработка данных: Справочное издание / С.А. Айвазян, И.С. Енюков, Л.Д. Мешалкин. – М.: Финансы и статистика, 1983. – 471 с.

2.Ветцель Е.С. Теория вероятностей. Учебник для вузов. − М.: Физматгиз, 1969.

3.Гмурман Е.В. Теория вероятностей и математическая статистика: Учебноепособиедлявузов. – Изд. 7-е, стер. – М.: Высшаяшкола, 2001. – 479 с.

4.Гнеденко Б.В. Курс теории вероятностей: Учебник. – Изд. 6-е, перераб. и доп. – М.: Наука. Главная редакция физико-математической литературы, 1988. – 448 с.

5.Загребаев А.М., Овсянникова Н.В. Автоматизированная обучающая система по физике реакторов: Учебное пособие. М.: МИФИ, 2002. – 160 с.

6.Климов А.Н. Ядерная физика и ядерные реакторы: Учебник для вузов. – 3-е изд., перераб. и доп. – М.: Энергоатомиздат, 2002. – 464 с.

7.Королюк В.С., Портенко Н.И., Скороход А.В. и др. Справочник по теории вероятностей и математической статистике. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 640 с.

8.Пугачев В.С. Теория вероятностей и математическая статистика: Учеб. пособие. – 2-е изд., испр. и доп. – М.: Физматлит, 2002. – 496 с.

106

ГЛАВА 2. СЛУЧАЙНЫЕ ФУНКЦИИ

ИИХ ХАРАКТЕРИСТИКИ

2.1.Общие свойства случайных функций

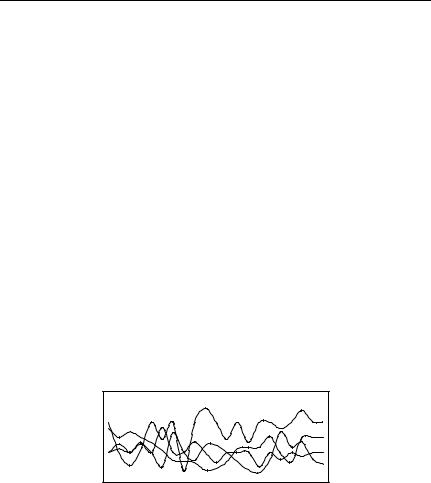
Функция X (t) называется случайной функцией (рис. 2.1), если

её значение при любом аргументе является случайной величиной [11, 12]. Аргумент t будем считать величиной неслучайной. Различают два случая:

1)аргумент функции может принимать любые значения в заданном интервале;

2)аргумент функции может принимать только дискретные значения.

В первом случае X (t) называют случайным процессом, во вто-

ром – случайной последовательностью.

Пусть проведено n независимых измерений функции. При каждом измерении она примет конкретный вид, который называется реализацией случайной функции. Для фиксированного значения аргумента t функция X (t) превращается в случайную величину.

Эта случайная величина называется сечением случайной функции. Для полной вероятностной характеристики случайной функции необходимо задать ее закон распределения, например F(x, t) . Та-

кой закон называется одномерным.

Рис. 2.1. Иллюстрация к понятию случайной функции

107

Одномерный закон распределения является достаточной характеристикой случайной функции только тогда, когда значения случайной функции при различных значениях аргумента рассматриваются изолированно друг от друга. Если этого условия нет, то необходимо рассматривать совместный закон распределения случайной функции при t1 и t2 . Закон распределения совокупности зна-

чений случайной функции при произвольных t1, ..., tn называют n-

мерным законом распределения. Зная его, можно получить закон меньшей размерности.

+∞ +∞

fm (x1, ..., xm ; t1, ..., tm ) = ∫ ... ∫ fn (x1, ..., xn ; t1, ..., tn )dxm+1 ... dxn .(2.1.1)

−∞ −∞

Если значения случайной функции X (t) при любых значениях аргумента t1, ..., tn являются независимыми, то

fn (x1, ..., xm ; t1, ..., tm ) = f1(x1, t1) f1(x2 , t2 ) ... f1(xn , tn ) . (2.1.2)

Т.е. исчерпывающей характеристикой случайной функции с независимыми значениями является ее одномерный закон распределения.

Примером случайных величин, исчерпывающей характеристикой которых является двумерный закон распределения, являются марковские случайные процессы. Марковским случайным процессом (или процессом без последействия) называется функция скалярной переменной X (t) (при t1 < t2 <... < th <... < tn ), если услов-

ный закон распределения случайной величины X (th ) зависит только от случайной величины X (th−1) и не зависит от случайных ве-

личин X (t1),…, X (th−2 ) .

Рассмотренный случай определения случайных функций на практике не всегда удобен. В большинстве случаев ограничиваются заданием числовых параметров этих законов, подобно тому, как случайная величина может быть иногда с достаточной для практики точностью охарактеризована своими числовыми характеристиками. Отличие заключается лишь в том, что эти числовые характеристики представляют собой не числа, а функции. Из бесконечного числа моментов случайной функции наиболее важными являются моменты первого и второго порядков.

108

Момент первого порядка определяется выражением

mx (t) = M[ X (t)] ,

(2.1.3)

где mx (t) – математическое ожидание случайной функции – есть

неслучайная функция, значение которой при каждом значении аргумента равно математическому ожиданию сечения. Через одномерную плотность вероятности математическое ожидание выражается следующим образом:

+∞
mx (t) = ∫ xf1(x, t)dx .	(2.1.4)
−∞
Наиболее часто используются центральные моменты:
+∞
D[ X (t)] = M[{X (t) − mx (t)}2 ] = ∫ {x(t) − mx (t)}2 f1(x, t)dx ;	(2.1.5)
−∞
K (t1, t2 ) = M [{X (t1 ) − mx (t1 )} {X (t2 ) − mx (t2 )}] =
+∞ +∞
= ∫ ∫ {x(t1 ) − mx (t1 )} {x(t2 ) − mx (t2 )} f2 (x1, x2 , t1, t2 ) dx1dx2 ,	(2.1.6)

−∞ −∞

где D[ X (t)] = Dx (t) – дисперсия случайной функции; K (t1, t2 ) = = Kx (t1, t2 ) – корреляционная функция случайной функции X (t) .

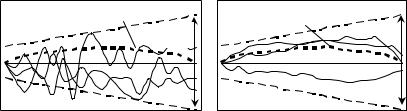
Из сравнения выражений (2.1.5) и (2.1.6) видно, что дисперсия является лишь «срезом» корреляционной функции при t1 = t2 = t . На рис. 2.2 показан качественный смысл введенных характеристик.

mx(1)	m(2)		Dx(2)
Dx(1)	x
а		б
Рис. 2.2. Реализация случайной функции D(1)	= D(2) ;	m(1)	= m(2)	:
x	x	x	x
а – слабая корреляция; б – сильная корреляция

109

Из рис. 2.2 видно, что хотя математические ожидания и дисперсии двух случайных функций X1(t) и X2 (t) совпадают, их харак-

тер совершенно различен. В первом случае зависимость между значениями случайной функции при различных аргументах гораздо слабее, чем во втором. Степень изменчивости функций характеризует корреляционная функция.

Если рассматриваются две случайные функции X (t) и Y (s) , то вводится понятие взаимной корреляционной функции:

Kxy = M[ X (t) Y (s)] = M[( X (t) − mx ) (Y (s) − my )] . (2.1.7)

Часто удобно использовать нормированные корреляционные и взаимные корреляционные функции:

′		′
		K (t, t )
r(t, t ) =			;		(2.1.8)
		′ ′
		K (t, t)K (t , t )
rxy (t, s) =		Kxy (t, s)		.	(2.1.9)
		Kx (t, t)K y (s, s)

Отметим, что понятие случайной функции обобщается и на комплексные случайные функции. При этом случайная функция представляется в виде: X (t) =U (t) + iV (t) , где U (t) и V (t) – веще-

ственные случайные функции, ординаты которых могут быть как независимыми, так и зависимыми случайными величинами. В дальнейшем комплексную случайную функцию будем обозначать

следующим образом X (t) . Отметим, что ниже в основном будут рассматриваться вещественные случайные функции.

Классификация случайных функций

Стационарные и нестационарные случайные функции

Различают стационарные и нестационарные случайные функции. Для стационарной случайной функции ее свойства не зависят от выбора начала отсчета, т.е. многомерные законы распределения зависят только от взаимного расположения моментов времени, но не от самих значений:

110