Загребаев Методы обработки статистической информации в задачах контроля 2008

	ˆ			1	2 −1
var{bLS (N ) −b} =					σηDu	.	(3.3.30)
				N

Последнее выражение показывает, что чем больше «разброс» входных параметров, тем точнее оценку мы можем получить. С другой стороны, чем больше дисперсия шума измерений, тем менее точную оценку мы получаем.

Пример. Рассмотрим идентификацию параметров линейного регрессионного объекта с тремя входами и одним выходом:

y(i) = b0 +b1u1 (i) +b2u2 (i) + b3u3 (i) + η(i) .

Для моделирования данного объекта были приняты следующие

истинные значения параметров:
b0 = 3.0; b1 = –4.0;	b2 = –5.0; b3 = –6.0.
Входные воздействия u1(i) ,	u2 (i) , u3 (i) , а также шум η(i) мо-

делировались с помощью генератора нормально распределенных псевдослучайных чисел.

Для идентификации параметров b0 , b1 , b2 , b3 и исследования

влияния дисперсии входных потоков и дисперсии шума на точность оценки было проведено 10 групп измерений по 50 измерений в каждой группе. В качестве характеристики точности оценивания использовалось вычисляемое средне квадратичное отклонение оценки от истинного значения параметра:

10

(b

ˆ

2

+ (b

ˆ

2

ˆ

2

+ (b

ˆ

2

/10 ,

S =

− b

)

− b

) + (b

− b

)

− b

)

∑

0

0 j

1

1 j

2

2 j

3

3 j

j=1

которое представляет собой приближение следа ковариационной матрицы ошибки оценки, т.е.

			ˆ		ˆ	т	S .
tr M (b − bLS )(b − bLS )

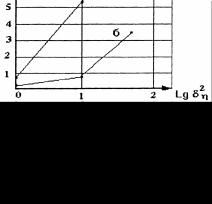
На рис. 3.3 приведены зависимости параметра точности S от дисперсий входных потоков при различных значениях дисперсии шума измерений. Полученные графические зависимости полностью согласуются с теоретическими выводами (3.3.30), а именно:

увеличение дисперсии входных потоков приводит к увеличению точности оценивания;

увеличение дисперсии шума измерений приводит к уменьшению точности оценивания.

191

Рис. 3.3. Зависимость точности оценки от дисперсии входных потоков и дисперсии шума измерений: а) δu = 50; б) δu = 1

Проверка адекватности модели и объекта по критерию Фишера [5] показала, что во всех расчетных случаях, кроме σu2 =1, ση2 = 50 , наблюдается адекватность модели объекту.

3.3.3. Рекуррентная форма метода наименьших квадратов для линейных регрессионных объектов

При решении практических инженерных задач оценивания на управляющих цифровых вычислительных машинах необходимо решение задач оценивания в реальном масштабе времени, что требует сокращения времени вычислений и объема обрабатываемой информации. Это может быть достигнуто как за счет совершенствования вычислительной техники, так и за счет модернизации алгоритмов оценивания в смысле уменьшения объема вычислений. Особенно трудоемкими операциями при использовании явных методов идентификации являются операции перемножения и обращения матриц большой размерности.

Учитывая это, можно заключить, что разработка методов оценивания, позволяющих снизить объем запоминаемой информации и уменьшить время вычислений, является актуальной задачей.

Во многих случаях, когда составляющие вектора измерений поступают последовательно с течением времени, возможно находить

192

оценку сˆ(i +1) на (i +1) -м шаге измерительного процесса в виде

коррекции оценки сˆ(i)		на i -м шаге. Эта коррекция представляет
собой взвешенную	невязку между векторами выходов объекта
′	′	′

y (i +1)	ˆ
	и модели ψ (U (i +1)c (i)) , полученными на интервале вре-

мени [ti ;ti+1] . Такие алгоритмы последовательной обработки дан-

ных называются рекуррентными (последовательными) алгоритмами и имеют вид:

	ˆ	ˆ		′			′ ′	ˆ
	с(i +1) = c (i) + K (i +1)( y (i +1) − ψ (U (i +1),c (i))) ,
′	– вектор поступивших на интервале [ti ;ti+1) измерений
y (i +1)
выхода размерности p ; U			′	(i +1)	– матрица входов, размерности

p ×m . Такой процесс получения последовательно уточняемых

оценок называется рекуррентным оцениванием.

В том случае, когда вся измерительная информация распадается на взаимно некоррелированные группы ( p измерений в группе),

для линейного регрессионного объекта вида

′	′		′	(3.3.31)
y (i +1)	=U (i +1)b + η (i +1) ,

можно сформировать рекуррентный алгоритм оценивания [4], при этом основные рекуррентные формулы для оценки параметров имеют вид:

ˆ	ˆ	′	′	ˆ
bLS (i +1)	= bLS (i) + K(i +1)( y (i +1)		−U (i +1)bLS (i)) . (3.3.32)
		′			(3.3.33)
	P(i +1) = P(i) − K (i +1)U		(i +1)P(i) .
Коэффициент усиления K (i +1)		может быть рассчитан по формуле

K(i +1) = P(i)U′т (i +1)(R′−1 (i +1) +U ′(i +1)P(i)U ′т (i +1))−1 . (3.3.34)

Часто в приложениях используется другая формула расчета коэффициента усиления K (i +1) :

′	′	(i +1) ,	(3.3.35а)
K (i +1) = P(i +1)U (i +1)R
′			p × p .
где R (i +1) – диагональная матрица весов размерности

Для инициализации рекуррентного процесса необходимо задать

начальные приближения ˆ и . Можно предложить два bLS (0) P(0)

способа задания начальных приближений:

193

первый способ заключается в использовании выборок U (0) , y(0) достаточного объема и последующем расчете начальных приближений по формулам [4]:

ˆ	= (U (0))	−1	y(0) ,	P(0) = (U	т	(0)R(0)U (0))	−1	; (3.3.35б)
bLS (0)

второй способ используется, если никаких предварительных выборок не производится. В этом случае можно предложить сле-

			ˆ
дующее правило: чем хуже начальные приближения bLS (0) , тем
больше должна быть матрица P(0) . Можно показать, что матрица
P(0) отражает матрицу ошибки оценки. Поэтому, чем хуже на-
чальное	ˆ		дисперсия ошибки
	приближение bLS (0) , тем больше
оценки,	и тем больше должна быть матрица P(0) . Вообще, матри-
цу P(0) можно задать в виде:
		P(0) = λI ,	(3.3.36)

где λ – большое число, при этом	ˆ	– любой вектор, размерно-
	bLS (0)

сти m.

Запишем полученные рекуррентные соотношения при одном измерении в группе для РАР-объекта, модель которого может быть представлена в виде:

					~	т	~
			~		y(i) = z		(i)c ,
	где	z(i) ,		определяются формулами (3.1.15), (3.1.16). В этом слу-
			c
	чае	оценка		ˆ	, матрица	усиления K (i +1) и матрица
				cLS (i +1)

P(i +1) рассчитываются по формулам:

ˆ	ˆ
cLS (i +1)	= cLS (i)

K(i +1) = P(i)z

+ K (i +1)(y(i) − z	т	ˆ
		(i)cLS (i)) , (3.3.37)

(i)			1	,	(3.3.38а)
		1
			+ z т (i)P(i)z(i)
	r(i)

или

K (i +1) = r(i)(P(i +1)z(i)) ,

(3.3.38б)

194

P(i +1) = P(i) −					1	P(i)z(i)z т(i)P(i) . (3.3.39)
		1		т
			+ z
					(i)P(i)z(i)
	r(i)

При равноточных измерениях не имеет смысла использовать

различные r(i) ,		i =1, 2, ... .		Тогда,		введя обозначение
H (i) = r P(i) , можно переписать				формулы		(3.3.38а),		(3.3.38б),
(3.3.39) в виде:				1
K (i +1) = H (i)z(i)								(3.3.40а)
			(1 + z т (i)H (i)z(i))
или		K (i +1) = H (i +1)z(i) ,						(3.3.40б)
H (i +1) = H (i) −		1			H (i)z(i)z т(i)H (i) .			(3.3.41)
(1		+ z т(i)H (i)z(i))
		ˆ		H (0) определяются так же, как
Начальные приближения c(0) ,

было рассмотрено выше.

Пример. Как показывает опыт использования рекуррентных соотношений (3.3.37) – (3.3.39), большое влияние на точность оценки и на скорость сходимости алгоритма оказывают начальные при-

ˆ	(0)	и матрицы P(0) .
ближения оценки c

Для исследования влияния этих факторов проводилась идентификация параметров линейного регрессионного объекта вида:

y(i) = b0 + b1U1(i) + b2U2 (i) +b3U3 (i) + η(i) .

При моделировании использовались следующие параметры объекта

b0 = 1.0; b1 = 2.0; b2 = 3.0; b3 = 4.0.

Входные потоки U j (i) ; i =1,50 ; j =1,3 , а также шум измерений η(i) моделировались с помощью генератора нормально распределенных случайных чисел с параметрами распределений:

M{U } =1,0 ;		σ2	=10,0 ;
1		U
		1
M{U	} = 2,0 ;	σ2	=10,0 ;
2		U2

195

M{U	} = 3,	0	;	σ2		=10,0 ;
3				U3
M{η} = 0,		0	;	ση2	=10,0 .

В качестве оценки точности определения параметров исследуемого объекта использовалась сглаженная по 10 реализациям ошибка

	1	10	3	ˆ	2		1/2
		∑ ∑
(i) =				(bj (i −l) −bj )		.
	10
		i=0 j=0
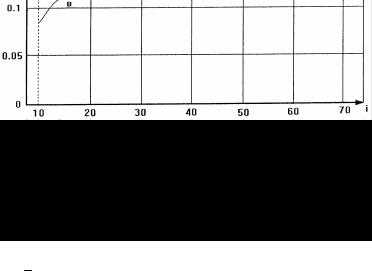
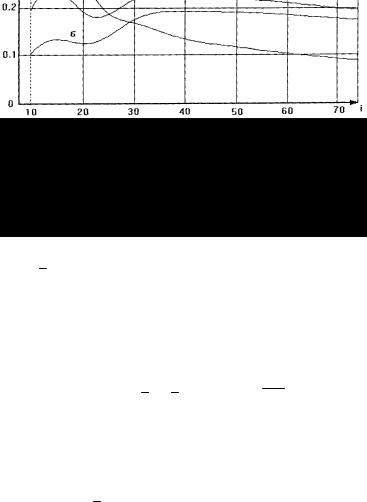
На рис.3.2а и 3.2б приведены зависимости							(i) от номера изме-
рений для различных начальных приближений H (0) при началь-
ных значениях оценки	ˆ		близких к истинным значениям пара-
	c(0)
метров (см. рис.3.4а) и плохих начальных приближениях								ˆ	(см.
								c(0)

рис.3.4б). Приведенные графические зависимости полностью согласуются с теоретическими выводами.

Рис. 3.4а. График зависимости сглаженной ошибки оценки от номера измерений при b (0) = [1,2; 2,0; 3,1; 3,9] и начальных приближениях матрицы Н(0):

а) Н[0] = 1хI; б) Н[0] = 10хI; в) Н[0] =100хI

196

Рис.3.4б. График зависимости сглаженной ошибки оценки от номера измерений при b (0) = [0; 0; 0; 0] и начальных приближениях матрицы Н[0]:

а) Н[0] = 10хI; б) Н[0] = 1000хI; в) Н[0] = 10000хI

3.3.4. Метод наименьших квадратов для нелинейных объектов

Рассмотрим нелинейный статический объект y(i) = Ψ(u (i),c) + η(i) , i =1, N .

Соответствующая ему модель представлена в виде

~		~			(3.3.42)
y(i) = Ψ(u (i),c ) , i =1, N .

Оптимизируемый критерий соответствует методу наименьших квадратов:

~

J (c )

	N						~			2
	= ∑[ y(i) − Ψ(u (i),c )]										r(i) :
	i=1					~
	ˆ
		= arg	~min J (c ) .								(3.3.43)
	cLS
			c

Задача минимизации критерия (3.3.43) при нелинейной функции (3.3.42) может быть решена каким-либо методом нелинейного программирования. Эти методы достаточно хорошо разработаны и описаны в соответствующей литературе.

197

В настоящем пособии приведен метод оптимизации, предназначенный для нахождения экстремума функции вида (3.3.43). Получаемая в результате итерационная последовательность соответствует методу Ньютона – Гаусса [14].

Пусть на j -м шаге итерационного процесса имеется некоторая

оценка параметра ˆ , достаточно близкая к истинному значению c( j)

параметра. Для каждого i -го момента времени ( i [i, N ] ) разложим функцию Ψ(u (i),cˆ( j)) в ряд Тейлора относительно оценки

ˆ до второго члена малости: c( j)

Ψ ~ (u (i),c )

Ψ ˆ

(u (i),c

			~
( j)) +	∂Ψ(u (i),c )
	∂c~т

~ − ˆ

(c c( j)) .(3.3.44)

~=ˆ

c c ( j)

Подставим последнее выражение в формулу критерия (3.3.43):

~ =

J (c )

N
			ˆ
= ∑				( j)) −
	y(i) − Ψ(u(i),c
i=1

Введем обозначения:

~~ ˆ

β( j) = с −с( j) ,

			ˆ	т
	∂Ψ(u(i),c )
	∂c					ˆ
					c	=c

y(1) e( j) =

y(N)

					2
			ˆ			r(i) . (3.3.45)
(c	−c			( j))
( j)
				ˆ
− Ψ(u (1), c( j))
	...							,
					ˆ
− Ψ(u (N ), c( j))

~

~

∂Ψ(u (1),c )

...

∂Ψ(u (1),c )

~

~

∂c1

~ ...

∂cm

~

. (3.3.46)

Φ( j) =

...

...

∂Ψ(

u

(N),c )

...

∂Ψ(

u

(N),c )

~

~

∂c1

∂cm

c~=

~

( j)

c

С учетом введенных обозначений, функция (3.3.45) принимает вид:

~	~		т		~
		( j))		R(e( j) −Φ( j)β( j)) . (3.3.47)
J (c ) = (e( j) −Φ( j)β

198

Последнее выражение, с точностью до обозначений, имеет тот

же вид, что и критерий (3.3.10). Минимизация критерия (3.3.47) по

~

β( j) приводит к итерационной последовательности:

cˆ( j +1) = cˆ( j) + (Φт ( j)RΦ( j))−1 Φт ( j)R( y − Ψ(cˆ( j))) . (3.3.48)

Необходимо отметить, что данный метод очень чувствителен к

ˆ	(0) .
выбору начального приближения c

Это объясняется тем, что в основе метода лежит линеаризация

		~	относительно оценки	ˆ	на j-м шаге итера-
функции Ψ(u (i),c )				c( j)

ционного процесса.

Признаком окончания итерационного процесса (3.3.48) может служить выполнение условия:

	ˆ	ˆ
	J (c( j +1))	− J (c( j))		≤ δ ,	(3.3.49)
	ˆ	+1))
	J (c( j

где δ – заданное малое число.

В заключение данного раздела сравним рекуррентную формулу (3.3.37) и итерационную (3.3.48). Несмотря на то, что эти формулы имеют схожий вид, они отражают два совершенно различных подхода к идентификации.

Рекуррентная формула (3.3.37) построена по принципу коррекции оценки на основе новых наблюдений.

Итерационная формула (3.3.48) обеспечивает движение к минимуму функции (3.3.43) по направлению антиградиента в точке

ˆ , при этом никаких новых наблюдений не поступает. c( j)

3.3.5.Линейные несмещенные оценки

сминимальной дисперсией ошибки оценки

(марковские оценки)

В случае, когда известна ковариационная матрица ошибки измерений Dη = var(η) , то рационально в качестве матрицы весов R в

методе наименьших квадратов использовать обратную ковариационную матрицу ошибок измерений, т.е.

R = Dη−1 .

199

Тогда критерий, соответствующий методу наименьших квадратов, для нахождения оценок линейного регрессионного объекта будет иметь вид:

т

D

−1

(3.3.50)

J (b ) = ( y − y(b ))

( y − y(b )) .

η

Подставляя R = D−1

в формулу оценки (3.3.13) и ошибки оцен-

η

ки (3.3.23) для линейного регрессионного объекта, получим

ˆ

= (U

т

−1

−1

U

т

−1

y

;

(3.3.51)

bMV

Dη U )

Dη

ˆ

(U

т

−1

−1

.

(3.3.52)

var(bMV −b ) =

Dη

U )

ˆ

является оценкой минимальной дис-

Покажем, что оценка bMV

персии в классе линейных оценок (теорема Маркова – Гаусса), т.е. покажем, что

ˆ

ˆ

−b ) ,

var(bL −b ) ≥ var(bMV

ˆ

– любая линейная несмещенная оценка.

где bL

ˆ

Запишем дисперсию оценки bL :

ˆ

т

} =

var(bL −b ) = M{(Qy

−b )(Qy −b )

= M{(QUb

+ Qη−

)(QUb

+ Qη−

)т} .

b

b

Учитывая, что для несмещенных оценок QU = I , получаем

ˆ

т

,

(3.3.53)

var(bL −b ) = QDηQ

где Dη — ковариационная матрица помехи. Рассмотрим два матричных выражения:

A = D−1/2U	и Bт = QD1/2	,
η	η
где
Dη = Dη1/2 (Dη1/2 )т .		(3.3.54)

Воспользуемся неравенством Шварца [14] для матриц. Согласно этому неравенству:

QDη1/2 (Dη1/2 )т Qт = QDηQт ≥

200