Загребаев Методы обработки статистической информации в задачах контроля 2008

Подставляя явный вид Y (iω) , получим

		Y1 =	f0	A(ω) exp(i[ωt + ϕ(ω)]).
			2
	Аналогичным образом для входного воздействия X2 =
=	f0	exp(−iωt) найдем
	2

Y2 = f20 A(ω)exp (−i[ωt + ϕ(ω)]).

Складывая Y1 и Y2 , получим следующий результат:

Y =Y1 +Y2 = f20 A(ω)[exp(iωt) exp(iϕ(ω)) + exp(−iωt) exp(−iϕ(ω))]=

= f20 A(ω) cos[ωt + ϕ(ω)].

Это выражение показывает, что вынужденные колебания, вызываемые в линейной динамической системе гармоническим воздействием, являются также гармонической функцией времени, отличающейся от входного воздействия лишь амплитудой и фазой (но с той же частотой).

Функция A(ω) называется амплитудной частотной характеристикой, ϕ(ω) – фазовой частотной характеристикой. P(ω) – вещественная частотная характеристика, Q(ω) – мнимая частотная характеристика.

Перейдем теперь к случаю, когда X (t) – случайная функция на интервале (0 ÷T ), т.е.

∞

X (t) = ∑ Wk exp(iωkt) .

k=−∞

Рассмотрим отдельное слагаемое этой суммы

Xk (t) =Wk exp(iωk t) .

Реакция системы на это воздействие будет

Yk (t) =WkY (iωk )exp(iωk t) .

131

Так как рассматриваем линейную систему, то согласно принципу суперпозиции реакция системы на сумму воздействий равна сумме реакций на каждое воздействие, т.е.

D		∞
Y (t)	=	∑ WkY (iωk ) exp(iωkt) .
		k=−∞
Или, обозначая WkY (iωk ) =Uk , получим:
D		∞

Y (t) = ∑ Uk exp(iωkt) ,

k=−∞

где Uk – некоррелированные случайные величины с математическими ожиданиями, равными нулю.

Определим спектр этого разложения. Для этого найдем D[Uk ]:

2

2

2

D[Uk ]= M Uk Uk

= M

WkY (iωk )

= M

Wk

Y (iωk )

=

=

Y (iω

)

2 M

W

2

=

Y (iω

)

2 D .

k

k

k

k

Таким образом, при преобразовании стационарной случайной функции X (t) , заданной на интервале от 0 до T линейной систе-

мой, каждая из ординат ее спектра умножается на квадрат модуля передаточной функции системы при данной частоте. Таким образом, при прохождении стационарной случайной функции через линейную стационарную систему ее частотный состав изменяется: некоторые частоты могут усиливаться, а некоторые – ослабляться (фильтроваться).

2.5.Примеры применения теории случайных функций

вфизике реакторов

2.5.1.Результаты статистической обработки реальных данных энергоблока с реактором РБМК (закон распределения, корреляционная функция

плотности потока нейтронов)

С целью обеспечения данными системы мониторинга параметров безопасности энергоблоков с реакторами РБМК-1000 в Кризисном центре концерна «Росэнергоатом» и в Локальном кризис-

132

ном центре Курской АЭС внедрено математическое обеспечение системы подготовки и передачи данных о состоянии реакторных установок.

Созданное программное обеспечение позволяет, помимо решения своих «штатных» задач, решать и задачи научного, перспективного характера, поскольку предоставляет исследователю детальную информацию о поведении в пространстве и времени важнейших параметров ядерного реактора. Поскольку решение задач идентификации часто требует знание законов распределения и моментных функций исследуемых параметров, то представляет интерес получения этих данных в реальном режиме эксплуатации реактора.

Приведенные ниже результаты получены при статистической обработке суточного файла состояния первого энергоблока Курской АЭС. Информация о параметрах снималась с периодичностью 2 – 3 мин. Целью статистической обработки было получение законов распределения, временных и пространственно-временных корреляционных функций [7].

Законы распределения поканальной мощности и расхода теплоносителя

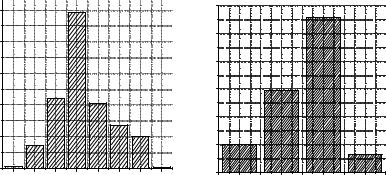
На рис. 2.10 и 2.11 в качестве примера показаны гистограммы распределения мощности для каналов в центре активной зоны и на краю соответственно.

Как видно из рис. 2.10 и 2.11, закон распределения мощностей различен. Анализ результатов обработки данных для всех каналов активной зоны выявил следующие закономерности.

Закон распределения поканальной мощности наиболее близок к нормальному в средней части активной зоны.

На нормальность закона распределения мощности в канале влияют расположенные рядом поглотители: закон распределения мощности близок к нормальному только в каналах, рядом с которыми расположены дополнительные поглотители (датчики, регулирующие стержни).

На краях активной зоны практически нет каналов с нормальным законом распределения мощности.

Анализ гистограмм распределения поканальных расходов показал, что в целом распределение поканального расхода теплоносителя во времени нельзя считать нормальным (гипотеза о нормаль-

133

ности закона распределения проверялась во всех случаях по критерию Пирсона при уровне значимости 0.05). Это характерно как для каналов, расположенных в центре активной зоны, так и для каналов, расположенных по краям. Однако так же, как и для поканальной мощности, существуют каналы, в которых закон распределения расхода теплоносителя близок к нормальному. Установлены следующие факты.

	0,25									0,6
	0,20									0,5
Относительная частота
									Относительная частота	0,4
	0,15
										0,3
	0,10
										0,2
	0,05									0,1
	0,00									0,0
	2,18	2,19	2,20	2,21	2,22	2,23	2,24	2,25
										0,815	0,820	0,825	0,830	0,835	0,840	0,845	0,850	0,855
			Мощностьканала, МВт
													Мощностьканала, МВт
Рис. 2.10. Гистограмма распределения									Рис. 2.11. Гистограмма распределения
	мощности в канале в центре									мощности в канале на периферии
		активной зоны
												активной зоны

На нормальность закона распределения расхода теплоносителя в канале влияют расположенные рядом поглотители: закон распределения расхода теплоносителя близок к нормальному только в каналах, рядом с которыми расположены поглотители (датчики, регулирующие стержни).

Закон распределения расхода теплоносителя в канале существенно не зависит от закона распределения мощности.

Распределение поканального расхода теплоносителя с большей степенью вероятности можно считать нормальным, нежели закон распределения поканальной мощности.

На погрешность определения закона распределения поканальной мощности и поканального расхода теплоносителя наибольшее влияние оказывают погрешности определения статистической оценки математического ожидания и дисперсии при выравнивании

134

статистических рядов. Были рассчитаны погрешности определения статистической оценки математического ожидания и дисперсии, которые как для поканальной мощности, так и для поканального расхода составили 4 %.

Определение временных автокорреляционных функций поканальной мощности и расхода

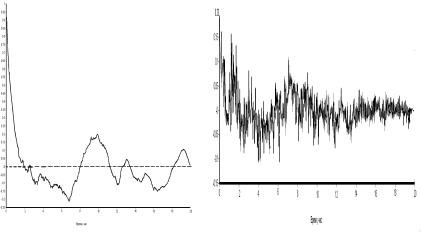
На рис. 2.12 и 2.13 показаны нормированные автокорреляционные функции поканальной мощности реактора и расхода через канал соответственно.

Рис. 2.12. Нормированная	Рис. 2.13. Нормированная
	корреляционная функция расхода
автокорреляционная функция	теплоносителя через канал
мощности канала

На рис. 2.12 присутствует ярко выраженный пик, соответствующий времени порядка 10 ч и, по-видимому, отражает факт обратной связи по ксенону.

Представленная на рис. 2.13 временная автокорреляционная функция расхода теплоносителя не имеет каких-либо ярко выраженных пиков при данной скважности измерений (примерно

2 мин).

135

Погрешность при определении автокорреляционной функции поканальной мощности и поканального расхода составила 8 %.

Определение пространственных корреляционных функций

иобластей сильной и слабой коррелированности

вактивной зоне

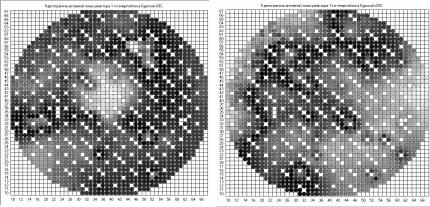
Пространственная автокорреляционная функция поканальной мощности реактора для каналов с законом распределения мощности близким к нормальному закону показана на рис. 2.14 и 2.15.

Рис. 2.14. Автокорреляционная функция мощности для канала в центре активной зоны

Рис. 2.15. Автокорреляционная функция мощности для канала на периферии активной зоны

Из анализа полученных в результате эксперимента графиков автокорреляционных функций, а также графика распределения дисперсии мощности по активной зоне, можно сделать вывод, что области коррелированности в активной зоне реактора качественно совпадают с областями перекоса поля нейтронов.

На рис. 2.16 показана пространственная автокорреляционная функция поканального расхода теплоносителя для каналов с законом распределения мощности, близким к нормальному закону.

На основе полученных в результате эксперимента данных можно сделать вывод, что области коррелированности для поканального расхода теплоносителя качественно совпадают с областями кор-

136

релированности для поканальной мощности, но степень коррелированности на порядок меньше.

Погрешности при определении автокорреляционной функции поканальной мощности и поканального расхода составили 9 %.

Автокорреляционная функция расхода для канала;316

0,0538839 0

Рис. 2.16. Автокорреляционная функция расхода для канала

вцентре активной зоны

2.5.2.Экспериментальное определение естественных функций реактора и их связь с собственными функциями

Опишем методику построения приближенного канонического разложения случайной функции плотности потока нейтронов в реакторе [3, 4, 5, 10]. Пусть в моменты времени t1, ..., t j , ..., tM в N

точках по объему активной зоны с координатами r1, ..., rN известны показания внутриреакторных датчиков C1 (t), ..., CN (t ). Тогда в

каждый момент времени по показаниям датчиков можно восстановить очередную реализацию плотности потока нейтронов, пользу-

137

ясь, например, методом наименьших квадратов. При этом, задавшись некоторым набором координатных функций Ψi (r ) (например, для высотного распределения принято использовать гармони-

ческие функции Ψi (z)= sin iHπ z ), будем искать оценку функции

ϕ(r, t) в следующем виде:

n
ϕˆ (r , t)= ∑Ai (t) Ψi (r )= AТ (t)Ψ(r ).	(2.5.1)

i=1

Сведем полученные коэффициенты аппроксимации в следующую таблицу:

Момент времени

Значения амплитуд

t

A1, ..., An

t1

A1(t1)

...

An(t1)

...

...

...

...

tj

A1(tj)

...

An(tj)

...

...

...

...

tM

A1(tM)

...

An(tM)

M

(t j )

M

(tj )

Среднее

∑ A1

…

∑An

по времени

j =1

j=1

A1 =

An =

M

M

Если теперь обработать данные таблицы на предмет определения корреляционных моментов между амплитудами, т.е. расчета величин

	M	(Ai (tp )−	Ai )(Aj (tp )−		j )
ˆ	∑			A
	p=1					,
Kij =
			M

то оказывается, что корреляционная матрица амплитуд

	K	K
	11	1n
K =
Kn1		Knn

может существенно отличаться от диагональной. Иными словами, коэффициенты при выбранных координатных функциях оказыва-

138

ются коррелированными. Интуитивно понятно, что этот факт означает неудачный выбор системы координатных функций. Если проводить аналогию с разложением функции в обычном математическом анализе, то это говорило бы о том, что выбранная система функций не является линейно независимой. Рассуждая с информационных позиций, можно представить себе, что информация о величине, например, первой гармоники, содержится не только в амплитуде первой гармоники, но и в остальных амплитудах. В теории

случайных функций известна процедура перехода от вектора A с

коррелированными составляющими к вектору A с некоррелированными составляющими [11]. Названная процедура аналогична

процедуре ортогонализации Грама − Шмидта, в ней исходный век-

G

тор A представляется в виде:

G	G	G	(2.5.2)
A = mA + Λ A ,

а элементы треугольной матрицы перехода Λ как раз и находятся из условия некоррелированности его координат. Если составить систему уравнений следующего вида:

K (Ai , Aj )= 0, i, j =		, i < j ,	(2.5.3)
	1, n

то, решив ее, можно получить рекуррентные выражения для вычисления элементов матрицы Λ :

1		0					0
a		1		0			0
	21
		a32		1 0				,	(2.5.4)
Λ = a31							0
	#						#
	#						0
		a			a
a			n2			nn−1	1
	n1

139

где

K (A1, Ai )

DA

ai1

=

, i

= 2, n;

1

j−1

D

Aj

= DA

j

− ∑a2jk DA , j =

1, n

;

k =1

k

1

j−1

aij =

K (Ai , Aj )

− ∑aik a jk DA

, i =

D

Aj

k =1

k

(2.5.5)

3, n, j = 2, i −1.

Из приведенных соотношений видно, что матрица перехода Λ

определяется статистическими характеристиками вектора A (а именно, его математическим ожиданием и корреляционной матрицей), оценки которых могут быть найдены по результатам описанного выше статистического эксперимента (то есть по набору реали-

заций вектора амплитуд A ). Подставив (2.5.4) в (2.5.2), получим:

ϕˆ (r )= AT Ψ(r )= (mA + Λ A)T Ψ(r )= mAT Ψ(r )+ AT (ΛT Ψ(r ))=

= mAT Ψ(r )+ AT Ψ(r )=

= Ψ0 (r )+ A1 Ψ1 (r )+ A2 Ψ2 (r )+... + An Ψn (r ),

(2.5.6)

где

Ψ0

(r )= mAT Ψ(r );

(r )+... + a

(r );

Ψ

1

(r )= Ψ

(r )+ a Ψ

2

n1

Ψ

n

1

21

(r )= Ψ

(r )+ a

Ψ

(r )+... + a

Ψ

(r );

Ψ

(2.5.7)

2

2

32

3

n2

n

Ψ

n−1

(r )= Ψ

n−1

(r )+ a

Ψ

n

(r );

nn−1

Ψ

n

(r )= Ψ

n

(r ).

Из выражения (2.5.6) видно, что коэффициентами аппроксимации реализации случайной функции ϕ(r ) набором функций

{ Ψk (r )} являются координаты вектора A с некоррелированными составляющими. Это означает, что функции { Ψk (r )}, определяе-

140