Загребаев Методы обработки статистической информации в задачах контроля 2008

Этот же результат можно получить проще, положив в спектральном разложении корреляционной функции τ = 0 .

Таким образом, дисперсия случайной функции равна сумме дисперсий всех гармоник ее канонического разложения.

На бесконечном участке времени спектральное разложение случайной функции проводится через интеграл Фурье. При этом четную корреляционную функцию с помощью интеграла Фурье записывают следующим образом:

∞
K (τ) = ∫ S(ω) cos ωτdω ,	(2.3.3)
0

где S(ω) называется спектральной плотностью стационарной случайной функции. При τ = 0 получим:

∞
K (0) = D = ∫ S(ω) dω.	(2.3.4)
0

Таким образом, спектральная плотность есть не что иное, как разложение дисперсии на сумму элементарных слагаемых S(ω) dω,

т.е. спектральная плотность есть разложение дисперсии по частотам. При известной корреляционной функции спектральная плотность получается из соотношения

		2	∞
	S(ω) =		∫ K (τ) cos ωτdτ.	(2.3.5)
		π
			0

На практике вместо спектральной плотности часто пользуются нормированной спектральной плотностью

s(ω) =	S(ω)	.	(2.3.6)
	D

Нетрудно видеть, что нормированная корреляционная функция и нормированная случайная плотность связаны соотношениями:

		∞
	ρ(τ) = ∫ s(ω) cos ωτdω ;				(2.3.7)
		0
		2		∞
	s(τ) =			∫ρ(τ) cos ωτdτ .	(2.3.8)
		π
				0

121

Комплексная форма спектрального разложения на конечном интервале имеет вид:

				+∞
	X (t) = ∑ Uk exp(iωkt) ;				(2.3.9)
				k=−∞
				+∞
K (τ) =				∑ Dk exp(iωk τ) ;	(2.3.10)
				k=−∞
		1		T
Dk	=			∫ K(τ) exp(−iωk τ) dτ.	(2.3.11)
		2T
			−T

На бесконечном интервале спектральное разложение в комплексной форме имеет вид:

		+∞
	X (t) = ∫ V (ω) exp(iωt)dω ,			(2.3.12)
		−∞
	где V (ω) – белый шум переменной ω, интенсивность которого
	равна спектральной плотности S (ω) :
	S (ω) =	1	+∞
			∫ K(τ)exp(−iωk τ) dτ.	(2.3.13)
		2π −∞

При этом корреляционная функция выражается через спектральную плотность следующим образом:

	∞
	K (τ) = ∫ S (ω) exp(iωk τ)dω.			(2.3.14)
	−∞
Свойства спектральной плотности.
1.	S(ω) ≥ 0 при любом ω.
	+∞
2.	∫ S(ω)dω< ∞ . При росте	ω	S(ω) → 0 .

−∞

3. Для вещественных случайных процессов S(ω) = S(−ω) , т.е

спектральная функция – четная функция.

Использование спектрального разложения является эффективным подходом при исследовании стационарных случайных процессов.

122

Примеры вычисления спектральной плотности стационарного случайного процесса.

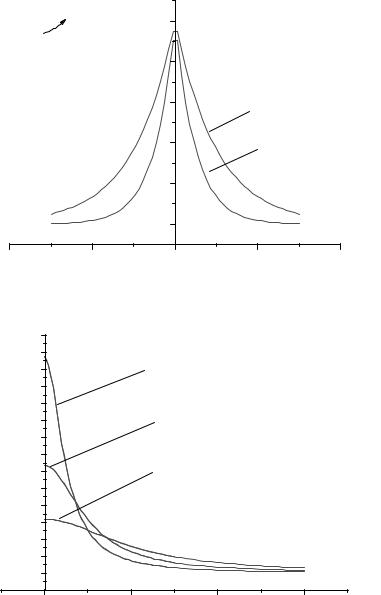
Пример 2.2. Найти спектральную плотность стационарного процесса, имеющего нормированную корреляционную функцию (рис. 2.4) вида

r(τ) = exp (−α τ ) .

Решение:

+∞

2

+∞

S(ω) =

1

∫ KX (τ)exp(−iωτ)dτ= σ

∫ exp(−iωτ−α

τ

)dτ=

2π

−∞

2π−∞

2 0

+∞

=

σ

∫ exp(ατ−iωτ)dτ+ ∫ exp(−iωτ−ατ)dτ =

2π

0

−∞

2

0

+∞

=

σ

∫ exp(

=

(α−iω)τ)dτ+ ∫ exp(−(iω+α)τ)dτ

2π

0

−∞

σ2

1

exp((α−iω)τ)

0

1

exp(−(α+iω)τ)

+∞

=

+ −

=

α−iω

2π

−∞

α+iω

0

σ2 1

1

σ2

2α

ασ2

=

2π

+

= 2π

=

.

(2.3.15)

α−iω

α+iω

α2 +ω2

π(α2 +ω2 )

При увеличении α корреляционная функция спадает быстрее, характер колебаний случайной функции становится резким и более беспорядочным.

При увеличении α функция спектральной плотности S(ω) ста-

новится более пологой, т.е. все больший вклад дают большие частоты (рис. 2.5).

При α → ∞ – белый шум.

123

	функция	1,0
		0,8
	кореляционная	0,6	альфа=1
		0,4	альфа=2
	нормированная	0,2
		0,0
-4	-2	0	2	4
		тау
	Рис. 2.4. Нормированная корреляционная функция

	0,70
плотность	0,65
	0,60		альфа=0.5
	0,55
	0,50
спектральная	0,45		альфа=1
	0,40
	0,35
	0,30		альфа=2
	0,25
нормированная	0,20
	0,15
	0,10
	0,05
	0,00
	-0,05
	0	2	4	6

Рис. 2.5. Нормированная спектральная плотность

124

Пример 2.3. Найти нормированную спектральную плотность случайной функции X (t) , если ее нормированная корреляционная

функция имеет вид

r(τ) = exp (−α τ )cosβτ.

Решение. Представим r(τ) в комплексной форме:

r(τ) = exp (−α		τ		)	exp(iβt) + exp(−iβt)	;
				2

1

+∞

S(ω) =

∫ r(τ) exp(−iωτ) dτ =

2π −∞

1

+∞

exp(iβt) + exp(−iβt)

=

−∞∫ exp(−iωτ) exp (−α

τ

)

dτ =

2π

2

1

0

=

∫ exp(−iωτ) exp (ατ)(exp(iβt) + exp(−iβt))dτ +

4π

−∞

+∞

+

exp(−iωτ)exp(

=

∫

−ατ)(exp(iβt) + exp(−iβt))dτ

−0

	1			α		α
=... =					+
							.	(2.3.16)
				+ (β+ ω)2		α2 + (ω−β)2
	2π		α2

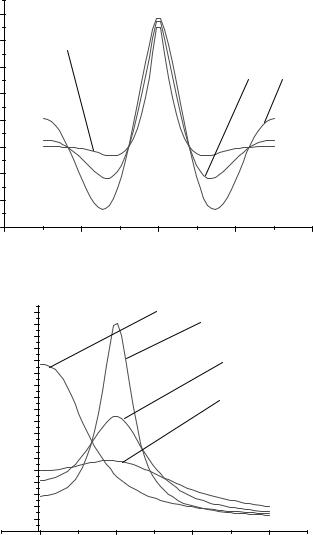
Вид графика спектральной плотности зависит от соотношения параметров α и β, т.е. от того, что преобладает в корреляционной

функции – убывание по закону exp(−α τ ) или колебания по зако-

ну cosβτ (рис. 2.6).

Очевидно, что при малых α преобладает колебание, при сравнительно больших α – убывание (рис. 2.7). В первом случае случайная функция близка к периодическим колебаниям частоты β со случайной амплитудой и фазой. Соответственно в спектре случайной функции преобладают частоты, близкие к β. Во втором случае спектральный состав случайной функции более равномерен, преобладания тех или иных частот не наблюдается. В пределе при

125

α → ∞ спектр случайной функции приближается к «белому» спек-
тру.
функция	1,0
	0,8	альфа=2
корреляционная	0,6			альфа=1 альфа=0.5
	0,4
	0,2
	0,0
нормированная
	-0,2
	-0,4
	-0,6
	-4	-2	0	2	4
			тау
		Рис. 2.6. Нормированная корреляционная функция

	0,34		альфа=1,в=0.5
	0,32			альфа=0.5, в=2
	0,30
	0,28			альфа=1,в=2
плотность	0,26
	0,24
	0,22
	0,20			альфа=2,в=2
	0,18
спектральная	0,16
	0,14
	0,12
	0,10
	0,08
	0,06
	0,04
	0,02
	0,00
	-0,02
	0	2	4	6
			тау
	Рис. 2.7. Нормированная спектральная плотность
			126

Пример 2.4. Найти корреляционную функцию стационарной случайной функции, спектральная плотность которой постоянна:

	s(ω) = s0 .
Решение:
∞	∞
ρ(τ) = ∫	sX (ω) exp(iωτ) dω= s0 ∫ exp(iωτ) dω= 2πs0δ(τ) .
−∞	−∞

Таким образом, стационарная случайная функция с постоянной спектральной функцией представляет собой белый шум. Физически это означает, что дисперсия белого шума равномерно распределена по частотам.

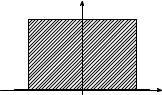
Пример 2.5. Спектральная плотность (рис. 2.8) стационарной случайной функции X (t) на участке от −ω1 до +ω1 постоянна, а вне его равна нулю:

a		при				ω		< ω ;
								1
S(ω) =	0	при				ω		> ω1.	(2.3.17)

Найти корреляционную функцию.

	S (ω)
	a
	ω
−ω1	ω1
Рис. 2.8 Спектральная плотность

Решение:

	∞	ω1	2a sin(ω1τ)
	K (τ) = ∫	S(ω) exp(iωτ)dω = 2a ∫ cos(ωτ)dω =		; (2.3.18)
			τ
	−∞	0

D = K (0) = 2aω1 .

127

2.4.Стационарные случайные процессы

вдинамических системах

Задача ставится следующим образом: требуется исследовать точность работы системы, описываемой дифференциальным уравнением

a		dnY		+a			dn−1Y		+... +a Y =
n dtn					n−1 dtn−1					0
=b		dm X			+b			dm−1X		+... +b X (t) ,	(2.4.1)
m dtmn						m−1 dtm−1				0

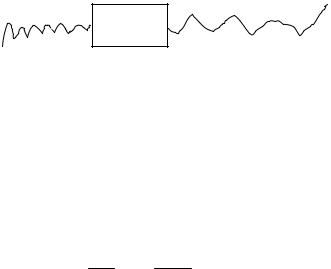
где на вход системы подается стационарная случайная функция X (t) (рис. 2.9) с известными свойствами (спектральным составом).

X (t)	Y (t)
	ˆ
	L
mx , Kx (τ)	m , K	Y	(τ)
	Y

Рис. 2.9. Преобразование случайной функции линейной системой

Напомним некоторые понятия из теории автоматического регулирования.

Решение или общий интеграл уравнения

		d n			d n−1
a	n			+ a			+... + a	Y
			n			n−1
		dt		n−1	dt		0

		d	m		d	m−1
= b				+ b				+... + b	X (t) ,
			mn				m−1
	m	dt		m−1	dt			0

если X – неслучайная величина, состоит из двух частей – из общего интеграла однородного уравнения

an d nY + an−1 d n−1Y +... + a0Y = 0 , dtn dtn−1

удовлетворяющего соответствующим начальным условиям, и частного решения неоднородного уравнения (т.е. такой функции, которая при подстановке в левую часть дает тождество).

Решение однородного уравнения ищем в виде:

Y (t) = exp(λt) .

128

При подстановке этого выражения в однородное уравнение получим:

(anλn + an−1λn−1 +... + a0 )exp(λ t) = 0 ,

т.е. выражение Y (t) = exp(λt) есть решение уравнения, если λ является корнем уравнения

anλn + an−1λn−1 +... + a0 = 0 .

Это уравнение имеет n корней: λ1, λ2 , ..., λn . Если λ1, λ2 , ..., λn различны, то

Y (t) = C1 exp(λ1t) +... + Cn exp(λnt) ,

где C1,C2 , ...,Cn определяются из начальных условий, при Reλi < 0

lim Y (t) = 0 ,

t→∞

т.е. свободные колебания системы затухают с течением времени. Найдем теперь частное решение уравнения для случая, когда

воздействие на входе системы представляет собой гармоническую функцию времени, например, следующего вида:

X (t) = f0 cos ωt .

X (t) можно представить в комплексной форме:

X (t) = f20 exp(iωt) + f20 exp(−iωt) .

Найдем эффект, создаваемый каждым из слагаемых. Начнем со слагаемого X1 = f20 exp(iωt) . Будем искать решение уравнения в виде

Y1 = f20 Y (iω)exp(iωt) .

Подставляя это выражение в левую и правую часть исходного уравнения, получим:

f20 (an (iω)n + an−1(iω)n−1 +... + a0 )Y (iω)exp(iωt) =

129

= f20 (bm (iω)m + bm−1(iω)m−1 +... + b0 )exp(iωt),

откуда

Y (iω) = bm (iω)m + bm−1(iω)−m−1 +...b0 . an (iω)n + an−1(iω)n 1 +... + a0

Функция Y (iω) называется передаточной функцией динамиче-

ской системы. Отделяя в числителе и знаменателе действительную и мнимую части:

Y (iω) = a(ω) + ib(ω) , c(ω) + id(ω)

где

a(ω) = b0 − b2ω2 + b4ω4 −... ; b(ω) = b1ω−b3ω3 + b5ω5 −... ; c(ω) = a0 − a2ω2 + a4ω4 −... ; d(ω) = a1ω− a3ω3 + a5ω5 −...

или

Y (iω) = P(ω) + iQ(ω) = A(ω) exp(iϕ(ω)) ,

где

P(ω) =		a(ω)c(ω) + b(ω)d(ω)						;
				c2 (ω) + d 2 (ω)
Q(ω) =		b(ω)c(ω) − a(ω)d(ω)							;
				c2 (ω) + d 2 (ω)
A = +				a2	(ω) + b2 (ω)		;
				c2	(ω) + d 2 (ω)
ϕ = arctg			b(ω)c(ω) − a(ω)d(ω)							.
			a(ω)c(ω) + b(ω)d(ω)

130