Загребаев Методы обработки статистической информации в задачах контроля 2008

2
1,5
1
0,5
0			х
-0,5	0	0,5		1
-1
-1,5
-2
		в) k = 3

2
1,5
1
0,5
0		х
-0,5 0	0,5		1
-1
-1,5
-2	г) k = 4

2
1,5
1
0,5
0			х
-0,5	0	0,5		1
-1
-1,5
-2

д) k = 5

Рис. 2.18. Окончание

151

Из рис. 2.18 видно, что качественный вид функций совпадает, а различие растет с возрастанием собственных чисел задачи. В табл. 2.1 показана относительная норма разности собственных функций невозмущенного реактора и оптимальных координатных функций канонического разложения в зависимости от степени уплощения (р) и номера функции. При этом относительная норма разности определялась по соотношению:

						h∫(ϕk − ψk )2dx
	δ				=	0	100 % .
						h
						∫ϕk2dx
						0

Таблица 2.1

Относительная норма разности собственных функций ϕn

и функций оптимального канонического разложения ψn в зависимости

от степени уплощения p, %

n			p
	0	0,2	0,4	0,6	0,8
1	1,35	0,0004	0,0003	0,0002	0,00001
2	6,86	0,94	0,64	0,28	0,14
3	37,53	8,91	4,68	1,56	0,09
4	59,50	23,16	14,42	4,34	1,43
5	83,03	40,59	29,63	10,05	1,98
6	105,36	57,56	46,08	19,92	5,08
7	100,11	72,86	61,22	32,93	7,44
8	108,54	81,44	76,35	49,13	15,11
9	61,61	92,62	96,06	65,24	23,98
10	64,83	78,61	78,37	76,16	36,55

Из табл. 2.1 видно, что с увеличением зоны «плато» различие между собственными функциями и функциями оптимального канонического разложения уменьшаются. В бесконечном реакторе с

152

некоррелированным шумом собственные функции будут совпадать с оптимальными координатными функциями канонического разложения. Этот вывод следует также из анализа уравнений (2.5.37) и (2.5.38), которые совпадают при ϕ0 = const (бесконечный реактор).

Проводились исследования функций оптимального канонического разложения, если возмущения носят коррелированный характер. Рассматривался гомогенный одномерный реактор, в котором корреляционная функция шума имела структуру вида

Kε = Dε exp(−β x − x′) . В этом случае в соответствии с выражением (2.5.22) корреляционная функция имеет вид

Kϕ (x, x′) = ∫ ∫G (x, x0 ) G (x′, x1 ) ϕ0 (x0 ) ϕ0 (x1 )×

V V

×Dε exp(−β			x0 − x1		)dx0dx1 ,
где функция Грина есть:
G(x, x0 ) = ∑			sin πkx sin πkx0			.
			H
k=2	(μk −μ1) ∫sin2 πkxdx
	0

Функции оптимального канонического разложения находились при решении методом Галеркина интегрального уравнения

H

λψ(x) = ∫ Kϕ(x, x′)ϕ0 (x′)ψ(x′)dx′ .

0

Результаты расчетов показали, что чем сильнее коррелированы возмущения, тем ближе функции оптимального канонического разложения к собственным функциям реактора.

В табл. 2.2 представлены результаты расчетов относительной нормы разности δ собственных функций и функций оптимально-

го канонического разложения в зависимости от степени коррелированности шумов.

Из табл. 2.2 видно, что при β > 50 коррелированный шум по

своему воздействию практически равноценен белому шуму. Физически это означает, что если корреляция между возмущающими

153

воздействиями уменьшается на расстоянии 501 характерного раз-

мера реактора в e раз (например, для реактора типа РБМК отноше-

ние шага решетки к диаметру активной зоны как раз порядка 501 ),

то для расчетов можно использовать приближение белого шума.

Таблица 2.2

Относительная норма δ разности собственных функций ϕn

ифункций оптимального канонического разложения ψn

взависимости от степени корреляции возмущений β, %

n				β
	0,05	0,5	5,0	50,0	500,0	5000,0
1	0,05	0,08	0,42	1,30	1.35	1,35
2	0,67	0,68	1,33	4,31	4.60	4,61
3	23,10	23,49	27,06	36,46	37,51	37,52
4	28,91	28,99	32,29	46,98	49,08	49,11
5	53,15	53,78	59,52	80,56	84,12	84,16
6	61,87	61,87	61,87	61,87	61,87	67,87
7	80,87	81,49	87,40	110,84	115,11	115,17
8	91,24	91,35	95,36	117,72	122,18	122,24
9	77,14	77,14	79,07	84,77	87,75	85,76
10	79,81	79,81	80,91	86,18	87,24	87,26

2.5.3. Вероятность образования локальных надкритических областей в активной зоне ядерного реактора

Как отмечалось ранее, в процессе эксплуатации ядерных энергетических реакторов в активной зоне возникают случайные возмущения размножающих свойств среды. Принципиально это может привести к тому, что в некоторой области активной зоны реактора возникнет флюктуация коэффициента размножения такой величины, что данная область становится надкритической (рис. 2.19) [1, 2, 6].

154

кэффициент размножения		δk
	β	δk=β
		Время
Рис. 2.19. Случайный выброс избытка коэффициента размножения

При наличии положительных обратных связей такая ситуация может стать опасной. В связи с этим возникает задача оценки вероятности образования локальных надкритических зон при флюктуации размножающих свойств среды.

Известно решение задачи по определению вероятного отклонения среднего избытка коэффициента размножения δk∞ =k∞ −1 в об-

ласти заданного размера S, содержащей N ячеек периодичности. При этом полагается, что δk∞ в отдельных ячейках реактора меня-

ется независимо в пространстве и времени. Понятно, что в реакторе, охваченном пространственно распределенными обратными связями, такое приближение не отражает реальной ситуации, и флюктуация коэффициента размножения представляет собой случайную функцию пространства и времени. В теории случайных функций известно решение «задачи о выбросах», позволяющее определить среднее число выбросов нормально распределенной стационарной случайной функции за данный уровень и параметры выброса [12].

Используя методику решения указанной задачи, определим вначале вероятность и среднюю длительность выброса избытка коэффициента размножения за некоторый уровень с без учета простран-

155

ственной составляющей (рассматривается реактор в «точечном» приближении или одна ячейка периодичности).

Предположим, что избыток коэффициента размножения δk∞ флюктуирует около своего математического ожидания k∞0 . Причем для δk∞ (t) как случайной функции времени известен закон ее

распределения.

Определим вероятность того, что на бесконечно малом временном интервале dt за моментом времени t произойдет выброс коэффициента размножения за уровень c. Для этого необходимо, чтобы имели место два события:

1)δk∞ (t) < c в момент времени t;

2)δk∞ (t + dt) > c в момент времени t + dt т.е. вероятность вы-

броса за уровень c есть P(δk∞(t) <c, δk∞(t + dt) >c).

Предполагая, что функция δk∞ (t) непрерывна, с точностью до бесконечно малых второго порядка, можно считать, что

δk∞ (k + dk) = δk∞(t) +V (t)dt ,

где V (t) = dδdtk∞ . Таким образом, условие δk∞ (t + dt) > c равносильно условию δk∞ (t) > c −V (t)dt . Тогда вместо двух условий вы-

броса коэффициента размножения за уровень c можно использовать одно условие:

c −V (t)dt < δk∞ (t) < c при V (t) > 0 .

Для определения вероятности выполнения этого неравенства введем в рассмотрение двумерный закон распределения ординаты случайной функции δk∞ и ее производной в один и тот же момент

времени f (δk∞, V | t) . Тогда для искомой вероятности выброса коэффициента размножения за уровень c получим:

∞	c
P(c−Vdt <δk∞ <c) =∫	∫ f (δk∞,V |t)dδk∞dV .

0 c−Vdt

Так как пределы внутреннего интеграла отличаются на бесконечно малую величину Vdt , то по теореме о среднем будем иметь:

156

c

∫ f (δk∞, V | t)dδk∞ ≈ dt V f (c, V | t) .

c−Vdt

Тогда

∞
P(c −Vdt < δk∞ < c) = dt ∫	f (c, V | t)VdV .
0
∞
Обозначим P(c | t) = ∫ f (c, V | t)VdV	– вероятность выброса в по-
0

ложительную область в единицу времени. Аналогичным образом можно получить и вероятность пересечения уровня δk∞ = c сверху вниз:

0

P′(c | t) = − ∫ f (c, V | t)VdV .

−∞

Пользуясь полученными выражениями, можно найти для любого промежутка времени T среднее время нахождения коэффициента размножения выше уровня c. Действительно, разобьем временной интервал T на n равных частей dt j , каждый их интервалов dt j рас-

положен вблизи координаты t j ( j =1, ..., n ). Вероятность того, что ордината случайной функции δk∞ > c равна

∞

P(δk∞(x j ) > c) = ∫ f (c | t j )dδk∞ .

c

Будем считать интервалы dt j настолько малыми, чтобы можно

было пренебречь случаями, когда внутри dt j функция δk∞ (t )	ме-
няет знак. Введем в рассмотрение систему случайных величин	j ,

каждая из которых равна соответствующему интервалу dt j или 0 в зависимости от того, будет ли в этом интервале δk∞ > c или δk∞ < c . Очевидно, что общее время пребывания избытка коэффициента размножения выше заданного уровня δk∞ > c , равно сумме

n

T = ∑ j . Для определения среднего суммарного времени T , в

j=1

157

пределах которого δk∞ > c , найдем математическое ожидание от обеих частей равенства

			n
	T		= ∑M[	j] .	(2.5.43)
			j=1
Поскольку случайная	величина			j может	принимать только
лишь два значения – dt j	или 0, то
			∞
M[ j ] = dt j ∫ f (δk∞ | t j )dδk∞ .					(2.5.44)
	0

Подставляя выражение (2.4.44) в (2.4.43) и переходя к пределу при n →∞ , получаем

		T ∞
		= ∫ ∫ f (δk∞ | t)dδk∞dt .	(2.5.45)
T
0 0

Для определения среднего времени превышения уровня с в течение одного выброса необходимо разделить T на среднее число выбросов N . Найдем среднее число выбросов N . Для этого, как и прежде, разобьем размер T на n равных интервалов dt j и введем

вспомогательные случайные величины N j . Величина N j = 0 , если в пределах dt j не было выброса, и N j =1, если выброс был. Полное число выбросов в течение времени T равно:

n

N = ∑ N j .

j=1

Применяя операцию математического ожидания к обеим частям равенства, получаем:

n

N = ∑ P(c, t j ) dt j .

j=1

Переходя к пределу при n →∞ , находим:

T ∞

N = ∫ ∫V f (c, V | t) dV dt .

0 0

158

Окончательно средний размер области с положительным выбросом материального параметра

						T ∞
						∫ ∫ f (δk∞ | t) dδk∞ dt
	T
τ =					=	0 0	.	(2.5.46)
						T ∞
	N
						∫ ∫V f (c, V | t) dV dt
				0 0

Для нормального процесса двумерная плотность распределения f (δk∞ , V ) распадается на произведение нормальных плотностей

распределения для δk∞ и V :

						1		−δk2∞
		f (δk∞,V) =						e	2σδ2k
						σδk	2π
2	= K (0) ;	2		d2			; K(τ)
где σδk		σV	=−		K(z)
				dz2
							0

1		−	V2
			2
		e 2σV ,
σ	2π
V

– корреляционная функция

случайной функции δk∞ ; τ= t −t′ – расстояние между моментами

времени t и t′.

На практике на небольших интервалах τ корреляционная функция K(τ) может быть аппроксимирована экспоненциальной струк-

турой вида

K(τ) = Dexp −α2τ2 ,

где параметр α характеризует степень корреляции; D – разброс параметра. При этом выражения для средней длительности выброса и среднего числа выбросов в единицу времени будут иметь вид

π

1

a2

[1−Φ(a)],

τ =

l

2

(2.5.47)

2 α

α

−

a2

N =

l

2 ,

(2.5.48)

π 2

где математическое ожидание числа выбросов в течение рассматриваемого промежутка T будет равно n = N T . Если последова-

159

	тельное появление выбросов считать независимыми редкими собы-
	тиями, то, используя закон Пуассона, можно оценить вероятность
	появления m выбросов в рассматриваемый промежуток времени:
	P	= n m l−n .
	m		m!
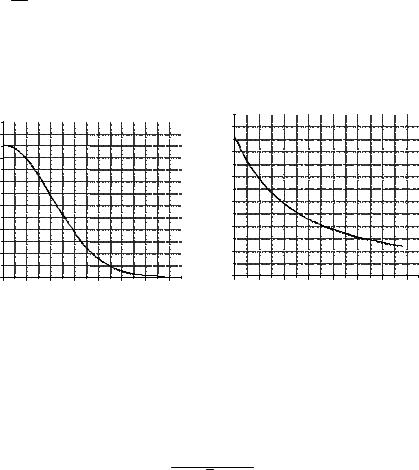
		На рис. 2.20 и 2.21 приведены номограммы для определения
	приведенных средних значений числа выбросов и длительности
	выброса от уровня выброса, позволяющие при известном α опре-
	делить данные величины.
,N/α
Среднее число выбросов в ед. времени	1,2									1,2
	1,0									1,0
	0,8									0,8
	0,6									0,6
	0,4									0,4
	0,2									0,2
	0,0									τ,Средняядлительностьвыбросас 0,0
	0,0		0,5	1,0	1,5	2,0	2,5	3,0	3,5	0,0	0,5	1,0	1,5	2,0	2,5	3,0	3,5
			Относительнаявеличинавыброса, a=c/σ								Относительнаявеличинавыброса, a=c/σ
Рис. 2.20. Зависимость приведенного										Рис. 2.21. Зависимость приведенной
		к α среднего числа выбросов								средней длительности выброса
	от относительного уровня выброса									от относительного уровня выброса

Оценим вероятность выброса избытка коэффициента размножения за уровень β = 0,0065 при случайных 5 % независимых возму-

щениях в температуре топлива, плотности теплоносителя и температуре воды для ячейки реактора РБМК на свежем топливе.

Расчеты показывают, что k∞max − k∞min = 0,635 % . Считая закон k∞

распределения δk∞ близким к нормальному, относительное сред-

нее

квадратическое

отклонение

можно

оценить

как

1

k∞max

− k∞min

= 0,00212 .

Тогда a =

β

≈ 3,0 ,

и при α =1

для

3

k∞

σδk

160