1.3.2. Правила построения кода Хэмминга

Коды Хэмминга являются линейными блочными кодами. При определенном построении они могут быть систематическими. Некоторые коды Хэмминга (не расширенные) являются циклическими.

Параметры кодов Хэмминга при m проверочных символах следующие:

- длина слова ;

- длина информационной части ;

- длина проверочной части ;

- минимальное кодовое расстояние .

Коды Хэмминга представляют собой один из немногих примеров совершенных кодов, для которых полностью известен спектр [4].

Код Хэмминга строится на основе задания проверочной матрицы. Проверочная матрица содержит m строк и (2^m-1) столбцов. Столбцы матрицы представляют собой набор двоичных чисел, записанных в возрастающем порядке. При этом столбцы, содержащие в наборе только одну единицу, являются проверочными, а столбцы, имеющие более одной единицы, - информационными.

Пример. Пусть , тогда длина слова, длина информационной части. Проверочная матрица кода Хэмминга (7,4) с тремя проверочными символами имеет вид:

.

(1.17)

Если переставить местами третий и четвертый столбцы, то проверочная матрица приобретет каноническую форму и код становится систематическим. Для построения порождающей матрицы, выполнения операции кодирования и вычисления синдрома можно воспользоваться правилами, описанными в п.1.3.1.

Код Хемминга с кодовым расстоянием позволяет исправить одну и обнаружить две ошибки. Если в кодовой комбинации произошла одна ошибка, то по виду синдрома легко можно определить, в какой позиции кодовой комбинации она произошла. Например, если ошибочно принят первый символ в кодовой комбинации, то это будет соответствовать синдрому 001, второй символ – синдрому 010, третий – синдрому 011 и т.д. Но в коде Хемминга с кодовым расстояниемимеется недостаток - по виду синдрома нельзя определить, одна или две ошибки имеются в кодовом слове. Чтобы избавиться от этого недостатка, необходимо увеличить кодовое расстояние.

Коды Хемминга можно превратить в коды с расстоянием 4, добавив дополнительную общую проверку на четность (т.е. добавив в кодовое слово символ, равный сумме по модулю 2 всех остальных кодовых символов). При этом код потеряет свойство цикличности, но по виду синдрома можно определить, сколько ошибок произошло в кодовом слове – одна или две.

1.3.3. Правила построения кода Рида-Маллера

Коды Рида-Маллера являются линейными двоичными блочными кодами. При определенном построении они могут быть систематическими. В общем случае коды Рида-Маллера не являются циклическими.

Коды Рида-Маллера задаются следующими параметрами для любых значений и, называемого порядком кода, меньшего, чем:

• длина кодового слова ;

• длина информационной части

• длина проверочной части

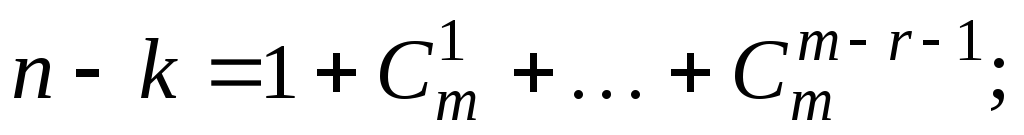
• минимальное кодовое расстояние .

Коды Рида-Маллера существуют в широкой области значений скоростей передачи и минимальных расстояний. Важным достоинством кодов Рида-Маллера является то, что они могут быть декодированы сравнительно простыми методами порогового декодирования.

Код Рида-Маллера определяется при помощи порождающей матрицы, состоящей из базисных векторов. Правило построения следующее:

• пусть - вектор, все компоненты которого равны 1;

• пусть - строки матрицы, столбцами которой являются все двоичные наборы длины. Код Рида-Маллера-го порядка содержит в качестве базиса векторыи все покомпонентные произведения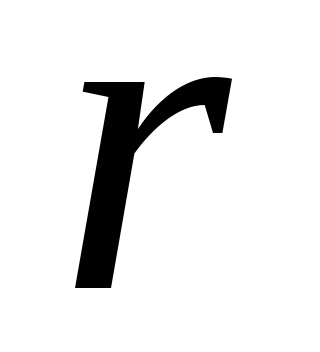или меньшего числа этих векторов.

Покомпонентное произведение любых двух векторов изадается следующим образом:

.

(1.18)

Пример. Для m = 4 и соответственно n = 2⁴ = 16 запишем базисные векторы кода Рида-Маллера:

Сформированная из базисных векторов порождающая матрица может быть использована для кодирования. Чтобы получить из данной матрицы проверочную, необходимо провести ее преобразование к систематическому виду. Это обеспечивается путем сложения по модулю 2 первой строки со всеми остальными строками матрицы. Такая операция не изменяет характеристик кода. Получив проверочную и порождающую матрицы, можно проводить с кодом все операции, описанные в п. 1.3.1. Следует отметить, что при декодировании методом порогового декодирования строить проверочную матрицу нет необходимости.