Тема № 8 .Парная нелинейная регрессия

Рассмотрим наиболее простые случаи нелинейной регрессии: гиперболу, экспоненту и параболу. При нахождении коэффициентов гиперболы и экспоненты используют прием приведения нелинейной регрессионной зависимости к линейному виду.

Гипербола

При нахождении гиперболы вводят новую переменную, тогда уравнение гиперболы принимает линейный вид. После этого используют формулы (9.3) для нахождений линейной функции, но вместо значенийиспользуются значения

; .

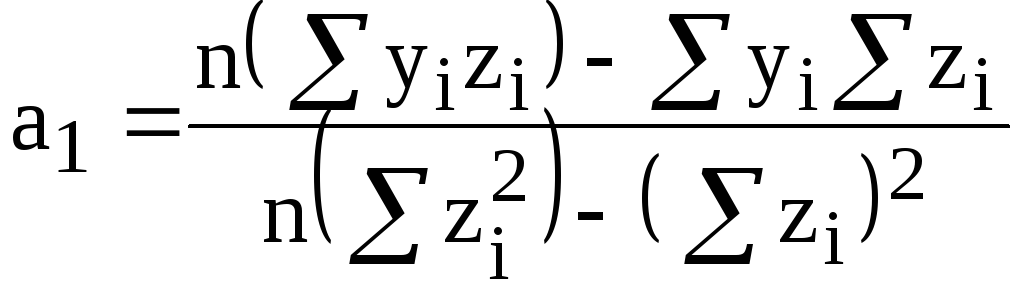При проведении вычислений во вспомогательную таблицу вносятся соответствующие колонки.

Экспонента

Для приведения к линейному виду экспоненты проведем логарифмирование

;

;

.

Введем переменные и, тогда, откуда следует, что можно применять формулы (9.3), в которых вместо значенийнадо использовать

.

При этом мы получим численные значения коэффициентов и, от которых надо перейти ки, используемых в модели экспоненты. Исходя из введенных обозначений и определения логарифма, получаем

, .

Парабола

Для нахождения коэффициентов параболы необходимо решить линейную систему из трех уравнений

Оценка силы нелинейной регрессионной связи

Сила регрессионной связи для гиперболы и параболы определяется непосредственно по формуле (9.2). При вычислении коэффициента детерминации экспоненты все значения параметра Y (исходные, регрессионные, среднее) необходимо заменить на их логарифмы, например, – наи т.д.

Основная литература: [4, С.53-114], [11, С.55-94] [10], [14]

Дополнительная литература: [20],[22],[23],[25], [32]

Тема № 9 Изучение взаимосвязей непараметрическими методами

Ранговая корреляция отражает статистическую связь между порядковыми переменными.

Методы ранговой корреляции основаны на использовании условной числовой метки, обозначающей место объекта в ряду всех анализируемых объектов, которые располагаются в порядке убывания исследуемого свойства. При этом под условной числовой меткой понимается ранг объекта по исследуемому признаку.

Последовательность рангов элементов вариационного ряда, указывающих на место объекта в ряду, называется ранжировкой.

Проектам, занявшим одинаковые места, присваиваются одинаковые ранги, равные текущему рангу в последовательности. Значение объединенного равно среднему значению рангов проектов с неразличимыми рангами.

Для измерения степени тесноты парной статистической связи между ранжировками К. Спирмен в 1904 году предложил показатель, который впоследствии получил название рангового коэффициента корреляции Спирмена.

Другим более трудоемким измерителем степени тесноты статистической связи между ранжировками является ранговый коэффициент корреляции Кендалла, который обладает большими удобствами при пересчете, если к статистическим объектам добавляются новые.

Основная литература: [5], [13,], [12,С.128-137]

Дополнительная литература: [20]

Тема № 10 Множественная линейная регрессия

Экономические показатели обычно зависят не от одного, а от нескольких факторов. Модель множественной линейной регрессии является обобщением линейной регрессии:

,

где у – зависимая переменная, х₁, х₂, ….х_к - объясняющие переменные, α, β₁, … β_к –коэффициенты регрессии, ε – случайная компонента.

Это уравнение можно записать в компактной форме в виде матрицы:

Y =Xβ +ε.

В модели множественной линейной регрессии метод наименьших квадратов представляет собой обобщение МНК для парной линейной регрессии.

Оцененное уравнение множественной линейной регрессии для всех наблюдений:

ŷ =α+β₁х_i1 + β₂x_i2+….+ β_kx_ik, i= 1,2,…,n

Оцененное уравнение в матричной форме: Ŷ =Xβ.

МНК заключается в определении коэффициентов оцененного уравнения из условия минимума суммы квадратов отклонений:

При практическом построении модели линейной регрессии существенен вопрос о значимости ее коэффициентов, вычисленных по конкретной выборке. Обычно формулируются гипотеза о равенстве коэффициентов нулю или о неравенстве. Если абсолютное наблюдаемое значение меньше или равно t-критического, то гипотеза принимается, т.е при определенном уровне значимости коэффициенты значимы.

Критерием качества уравнения регрессии выступает разброс случайной величины у в выборке, на основе которого определяется коэффициент детерминации. Он представляет собой долю вариации зависимой переменной у, объясненную с помощью оцененного уравнения регрессии.

Для оценки значимости коэффициента детерминации используется F-статистика Фишера.

Выдвигается гипотеза о равенстве всех коэффициентов регрессии нулю, при этом альтернативная гипотеза, хотя бы один из коэффициентов отличен от нуля.

Наблюдаемое значение, имеющее распределение Фишера, для множественной регрессии: . Оно сравнивается с критическим значением (таблица Фишера), если наблюдаемое значение больше критического, то коэффициент детерминации считается значимым при выбранном уровне значимости.

Мультиколлинеарность – это значит коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Следствием мультиколлинеарности является незначимость коэффициентов регрессии. Для определения сильно коррелированных переменных используется матрица частных коэффициентов корреляции. Способы устранения мультиколлинеарности: исключение из уравнения одной или нескольких объясняющих переменных, преобразование переменных.

Кроме проверки значимости коэффициентов и качества уравнения регрессии, необходима проверка выполнения условий Гаусса-Маркова, обеспечивающих несмещенность и эффективность оценок параметров регрессии.

Третье условие Гаусса-Маркова – независимость случайных членов в разных наблюдениях. Если нарушается это условие, т.е. существует связь между случайными переменными, то возникает явление автокорреляции.

В случае положительной автокорреляции, реализация случайного члена ε_І для ряда последовательных наблюдений смещают значения зависимой переменной в одном направлении, затем для последовательных наблюдений – в противоположном направлении, потом снова в первоначальном направлении и т.д. При отрицательной автокорреляции каждая реализация случайного члена ε_І, как правило, сменяется реализацией случайного члена ε_І+1 противоположного знака.

Для обнаружения автокорреляции используется статистика Дарбина - Уотсона: DW = 2 (1-r₁).

При положительной автокорреляции DW ≈ 0, при отрицательной DW ≈ 4, при отсутствии DW ≈ 2. Указывают нижнюю и верхнюю границы для критических значений статистики Дарбина - Уотсона. Автокорреляция первого порядка отсутствует, если статистика DW попадает в интервал (d_u, 4-d_u). Критерий Дарбина –Уотсона неприменим для моделей, включающих в состав объясняющих переменных лаги зависимой переменной.

Автокорреляцию первого порядка можно устранить простой манипуляцией с моделью.

Выполнение второго условия Гаусса-Маркова - постоянство дисперсии случайного члена ε_І – это случай гомоскедастичности.

Если дисперсия случайного члена меняется от наблюдения к наблюдению, то мы имеем дело с гетероскедастичностью. При гетероскедастичности оценки коэффициентов регрессии несмещенные, но неэффективные, следовательно, коэффициенты регрессии не будут значимыми. Для обнаружения гетероскедастичности используются тест Голдфелда – Квандта, а также взвешенные и логарифмические регрессии.

Если дисперсия случайного члена меняется от наблюдения к наблюдению , то мы имеем дело с гетероскедастичностью.

Основная литература: [4, С.90-175], [10], [14]

Дополнительная литература: [20],[22],[23],[25], [32]

Тема №11 Анализ временных рядов

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Общие виды моделей временного ряда

Аддитивная модель имеет вид: Y=T+S+E;

Мультипликативная модель: Y=T*S*E.

Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и Е для каждого уровня ряда. Построение модели включает следующие шаги;

1) выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты 5;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (Т + Е) или в мульти­пликативной (T*Е) модели;

4) аналитическое выравнивание уровней (Т + Е) или (Т*Е) и расчет значений T с использованием полученного уравнения тренда;

5) расчет полученных по модели значений (T+S) или (Т • S);

6) расчет абсолютных и/или относительных ошибок.

1. Гладкий ряд - возрастающий или ряд убывающий ряд в виде прямой линии, а также ряд с ускорением или замедлением.

Гладкость ряда означает отсутствие случайных, сезонных или циклических колебаний. Примерами таких рядов являются демографические ряды, а также ряды в сфере производства и торговли, связанные с демографическим фактором. Например, такие продукты, как соль, сигареты, зубная паста покупаются даже в случае потери работы и потребляются независимо от сезона года. 2. Временной ряд с сезонными колебаниями или с сезонным компонентом S. Прямая линия, сглаживающая временной ряд, является трендом T этого ряда. Сезонный компонент возникает, например, при рассмотрении уровня потребления газа, спроса на теплую обувь, которые зимой будут выше, чем в летние месяцы.

Основная литература: [4, С.90-175], [10], [14]

Дополнительная литература: [20],[22],[23],[25], [32]