1.4. Дискретное представление развивающейся гдс

Все исследуемые объекты, процессы и явления можно условно разделить на два больших класса.

1. Дискретизируемые объекты, представляющие собой перечислимую совокупность взаимосвязанных компонентов, которые могут рассматриваться как элементы системных моделей этих объектов. Например: группы людей, кристаллические образования, семиотические конструкции, алгебраические множества, категории, группы и др.

2. Непрерывные (неделимые, недискретизируемые) процессы, явления и объекты, в которых в явном, четко определенном виде нельзя выделить составляющие компоненты. Например: явления в электромагнитных полях, растворы, аморфные образования, жидкости, человеческие эмоции, прокатное производство и т. д. Здесь разделение на отдельно рассматриваемые элементы приводит к невосполнимым потерям в понимании сути анализируемых явлений.

Инвариантное моделирование, базирующееся на теории ГДС, дает возможность по мере необходимости строить системную модель как в дискретной, так и в волновой форме представления, сообразуясь с целями конкретного исследования, а также показывает и обосновывает взаимосвязь двух способов представления объектов — дискретного и полевого.

Раскроем содержание одной из разновидностей дискретного представления ГДС-моделей. Для этого рассмотрим матричный способ описания ГДС, основанный на применении гиперкомплексных матриц, впервые введенных для описания сложных систем в теории ГДС [20].

Запишем гиперкомплексную матрицу для простейшей ГДС, изображенной на рис. 1.5, где А₁ и А₂ — элементы ГДС, а у₁₂ и у₂₁, — взаимодействия между этими элемента ми. Получим матрицу системы S:

В (1.33) на главной диагонали стоят элементы матрицы, отображающие наличие и свойства элементов системы S. Заполнение диагонали выполняем по правилу

где а_nn — матричный элемент (диагональный), стоящий на пересечении n-го столбца и п-й строки; А_n (S) — п-й элемент системы S.

Слева и справа от главной диагонали располагаются матричныеэлементы, отображающие взаимодействия между элементами системы и определяемые по правилу

где а_nm — элемент матрицы, стоящий на пересечении n-й строки и m-го столбца; у_nm — взаимодействие элемента А_n с элементом А_m системы S в направлении от А_n к А_m.

Порядок матрицы определяется числом элементов и иерархических уровней системы S. В данном случае порядок матрицы N = 2 (гак как ГДС, изображенная на рис. 1.5, содержит два элемента одного иерархического уровня).

Более конкретную форму записи элементы матрицы приобретают в условиях определенного исследования.

В рамках инвариантного моделирования, при абстрактном анализе системных свойств, без наполнения их конкретным содержанием частного исследования, элементы гиперкомплекспоп матрицы наиболее удобно записывать с помощью М-чисел, впервые введенных в теории ГДС специально для описания сложных систем в работе [22]. При этом элементы на главной диагонали в матрице приобретают статус гиперкомплексных единиц и записываются А_nn = 1.

В данном изложении, целью которого является демонстрация принципиальной возможности дискретного описания ГДС, ограничимся наиболее общими элементами формализации, используемыми в теории ГДС.

Более подробно системные особенности элементов гиперкомплексной матрицы представлены в гл. 2 и 3.

Следует отметить, что описание ГДС с помощью гиперкомплексной матрицы, хотя и наиболее системоемкое, однако не единственно возможное, используемое для формализованного представления ГДС. Для той же цели (особенно для описания отдельно рассматриваемых системных инвариант и закономерностей) могут использоваться методы частных наук: вероятностный подход, теоретический аппарат дискретной математики и т. д. В частности, возможность применения алгебраических групп для описания ГДС показана в работе [18].

Рассмотрим более сложный пример, учитывая изложенные особенности гиперкомплексной матрицы, которую в теории ГДС часто называют матрицей взаимодействий и обозначают символом Y. Для этого запишем и проанализируем гиперкомплексную матрицу сложной ГДС с тремя иерархическими уровнями, представленную на рис. 1.6, где символами A_i,j,k обозначены элементы различного иерархического уровня системы S, а у_{(i,j,k)(m,n,r)} —взаимодействия между этими элементами.

З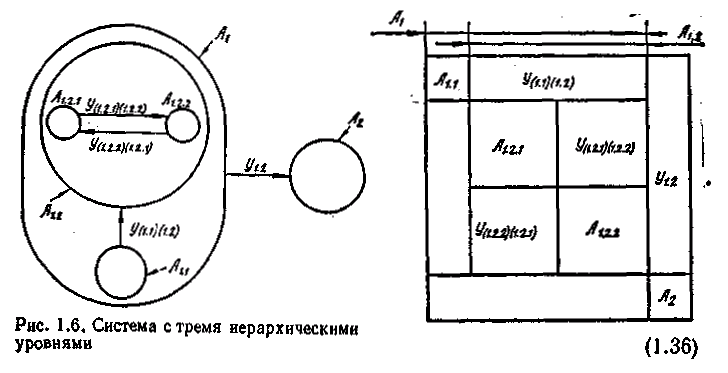апишем матрицу взаимодействийY системы S:

Вматрице (1.36) имеем по два элемента на каждом из трех иерархических уровней α, β, γ.

В соответствии с (1.37), по правилам теории ГДС, порядок N гиперкомплексной матрицы Y с тремя иерархическими уровнями запишется в виде многомернойдроби [20]:

где N (α) = 2 — число элементов на иерархическом уровне α, N(α), N(β), N(γ) = 2 определяются аналогично.

Покажем взаимосвязь матрицы Y с изложенными ранее порядком определения системы S и R-принципом.

Вобщем случае элементы матрицыY зависят от времени, отображая процесс развития

В соответствии с (1.38), анализируя процесс системной реализации, изложенный в 1.3, получаем условия, при которых матрица Y будет отображать основные фазы процесса системной реализации.

1. Фаза развития

Дифференцирование проводится по всем системным инвариантам, в частности

9. Стационарный режим

Расшифровывается аналогично фазе развития.

10. Фаза распад?

Анализируя гиперкомплексную матрицу исследуемой системы можно построить соответствующую этой системе кривую процесса системной реализации.

Очевидно, что выражения (1.39) — (1.41) отображают идеализированную ситуацию для простейшего случая процесса системной реализации. Являясь абсолютно верными для отображения сути сиюминутного (мгновенного) состояния системы, каждое из указанных условий может присутствовать (в качестве флюктуации) в каждой из фаз процесса системной реализации. Например, если процесс системной реализации идет не по явно выраженной линии, а путем колебаний, то даже на протяжении одной фазы можно будет найти такие отрезки времени, для которых будут справедливы указанные условия.

Относительно определения системы следует отметить: если для описания системы применяется гиперкомплексная матрица, то при выполнении операций с ней необходимо указывать (индексом при соответствующем символе) тот иерархический уровень, на котором надо выполнить требуемую операцию. Например, рассмотрим процедуру получения системного свойства S₃ (структурности) для системы S, описываемой матрицей (1.36). При этом нас будет интересовать не вся система, а только ее часть, которая находится на втором (β) и третьем (γ) иерархических уровнях. Символически указанную задачу и ее решение можно записать в виде

где индекс (0, β, γ) в общем (буквенном) виде, а индекс (0, 1, 1) с цифровой форме записи указывает, что операцию выделения графа из системы необходимо выполнять только для иерархических уровней β и γ Р, минуя уровень α (вместо α ставим нуль на соответствующем месте индекса). В (1.42) единицы обозначают наличие элемента или связи в анализируемой системе, а нуль (часто не пишется) — их отсутствие. Выражение (1.42) можно рассматривать как матричную форму записи искомого графа. При необходимости на основе (1.42) легко построить графическое отображение найденной системной характеристики — свойства структурности.

Отвлекаясь от ГДС-содержания, можно отметить, что гиперкомплексная матрица (по своей форме) совпадает с обычной квадратной матрицей, используемой в классической математике, если исследуемая ГДС, отображаемая этой матрицей, имеет только один иерархический уровень [12].

Использование матричного описания систем особенно удобно (в силу легкой алгоритмизуемости) при реализации методов теории ГДС с помощью ЭВМ.