Рекомендації щодо оброблення результатів у пакеті MathCad

Пакет MathCAD має достатній арсенал засобів роботи з матрицями. Зокрема, що стосується розв’язання СЛАР, то для перевірки вимог щодо визначення, чи має система розв’язання, можна використовувати функцію rank(A) – обчислення рангу матриці та оператор – обчислення визначника матриці коефіцієнтів.

Чисельне розв’язання СЛАР у пакеті MathCAD можна здійснити різноманітними засобами. Зокрема, СЛАР можна розв’язати матричним методом за допомогою запису (2.3), а також убудованими функціями: lsolve(A,B) і rref(D), де параметри A і B відповідають параметрам рівняння (2.3). Функція rref(D) реалізує прямий та зворотний хід методу Ґаусса [5, 6].

Крім того, у пакеті MathCAD можна отримати розв’язання СЛАР ітераційними методами, реалізуючи їх як засобами пакета, так і звичайним математичним записом. Однак слід зазначити, що реалізація останнього засобу в пакеті MathCAD не є ефективною (далі як демонстрацію наведено приклад організації ітераційного методу засобами пакета).

Для реалізації першого засобу (вбудованими можливостями) розв’язання СЛАР можна використовувати так званий "обчислювальний блок" з директивою Given та функціями Find, Minerr¹. Обчислювальний блок починається службовим словом – директивою Given і має таку структуру [5, 6]:

Given

Рівняння

Обмеження

Вирази з функціями Find або Minerr

У блоці використовується одна з двох функцій:

Find(v1,v2,…,vn) – повертає значення однієї або кількох змінних для точного розв’язання;

Minerr(v1,v2,…,vn) – повертає значення однієї або кількох змінних для наближеного розв’язання.

Між цими функціями існує принципова різниця. Перша функція намагається знайти точне розв’язання. Друга функція намагається знайти максимальне наближення до точного розв’язання (навіть до неіснуючого розв’язання) шляхом мінімізації середньоквадратичної похибки розв’язання. Для обчислення та перевірки збіжності ітераційного процесу (тобто обчислення норми матриці) можна застосувати одну з передбачених функцій пакета (наведені у тій самій послідовності, як і вище):

norm1(A), norm2(A), norme(A).

Слід зауважити, що розв’язання СЛАР з використанням обчислювального блока залежить від значення змінної TOL (точність, з якою пакет виконує обчислення).

Приклади виконання самостійної роботи

Приклад 1. Розв’язати СЛАР методом Ґаусса:

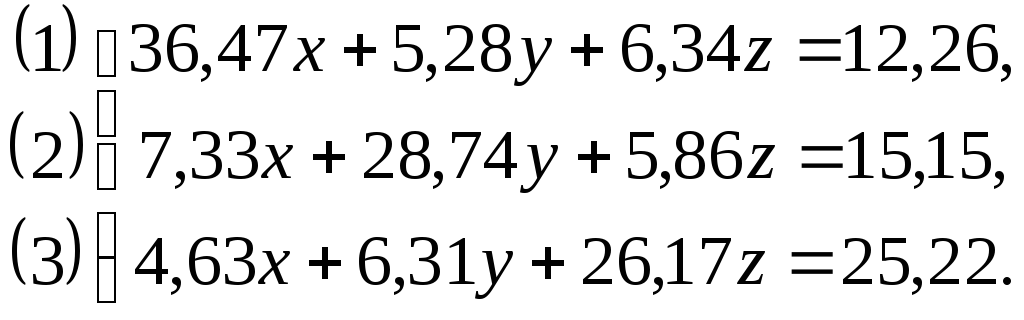
Розв’язок

Розділивши рівняння (1) на коефіцієнт при цього рівняння, отримаємо

. (2.14)

Помножимо рівняння (2.14) на коефіцієнт при рівняння (2) і результат віднімемо з (2). Отримаємо

.

Помножимо рівняння (2.14) на коефіцієнт при рівняння (3) і результат віднімемо з (3). Отримаємо

.

Таким чином, система рівнянь має вигляд:

Розділивши рівняння (4) на коефіцієнт при цього рівняння, маємо:

(2.15)

Помноживши рівняння (2.15) на коефіцієнт при рівняння (5) і віднявши з (5), отримуємо:

.

Отже, . Тоді,.

Приклад 2. Привести задану систему до вигляду, придатного для застосування методу ітерацій:

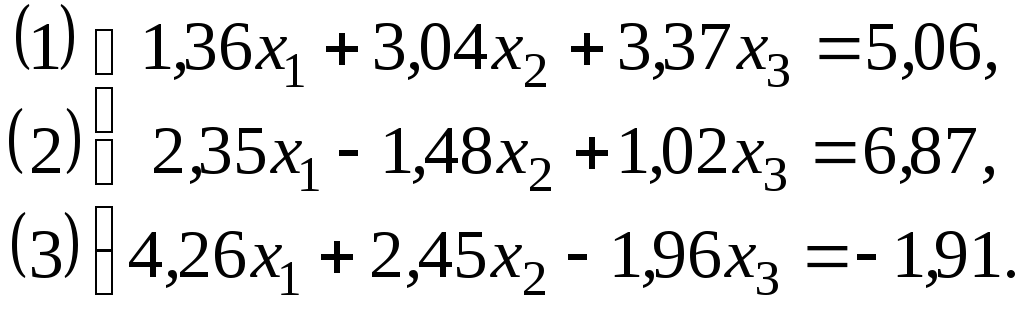(2.21)

Знайти приблизне розв’язання системи з точністю .

Розв’язок

Система (2.21) не містить рівнянь з коефіцієнтами, модулі яких більше суми модулів інших коефіцієнтів рівнянь. Шляхом еквівалентних перетворень приводимо задану систему до вигляду:

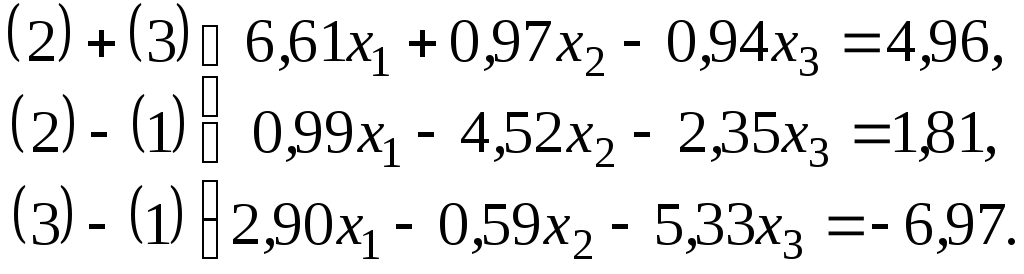(2.22)

Перед кожним рівнянням системи (2.22) відносно , друге – відносно, третє – відносно, отримаємо систему вигляду

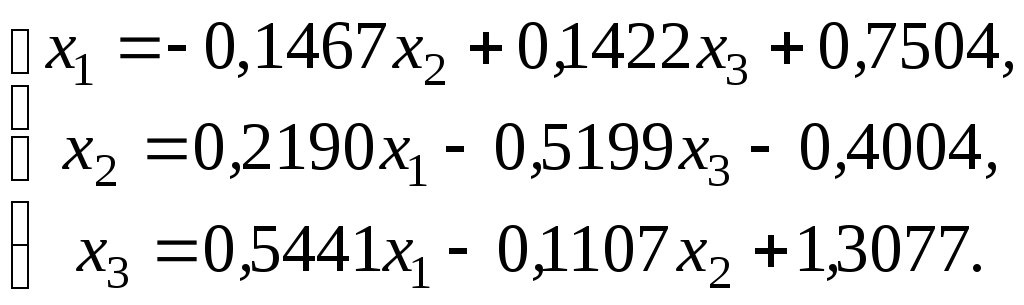(2.23)

Обчислимо норму матриці А системи (2.23)

.

Перевіряємо достатні умови збіжності методу простої ітерації за умови: , отже, збіжність за методом ітерацій ґарантовано.

Перевіряємо умови припинення ітераційного процесу. Використовуючи (2.10), отримуємо

Знаходимо наближене розв’язання системи методом простої ітерації. Візьмемо як початкове наближення стовпець вільних членів, тобто

;;.

Підставляючи ,,до правої частини системи (2.23), отримуємо ,,.

Продовжуючи ітераційний процес, при маємо:

;;.

При :

;;.

Знаходимо модулі різниць при,:

Обчислення можна припинити при , оскільки вказані оцінки свідчать про досягнення необхідної точності. Як розв’язання візьмемо:

;;.

Приклад 3.Розв’язати СЛАР прямими методами засобами пакета MathCAD.

Розв’язок

Приклад 4. Розв’язати СЛАР ітераційними методами засобами пакета MathCAD.

Розв’язок

Приклад 5. Розв’язати СЛАР за допомогою обчислювального блока пакета MathCAD.

Розв’язок