§2. Угол параллельности

Пусть а- прямая, М- точка, не лежащая наа. Опустим перпендикуляр наа:MNa. Обозначим прямуюа: АВ, так, чтобы А-N-В.!EF//BAи! СD//АВ

Утверждение 1FMN=DMN.

Доказательство: Ясно, чтоEFи СDразличные прямые т. к. эти углы меньше прямого. Это следует из док–ва теоремы, что точка, производящая сечение, лежит междуNи Р. Доказательство легко проводится от противного: ПустьDMN>FMN. Рассмотрим луч МF^/симметричный МFотносительно МN, т.е. отложим в другой полуплоскости угол, равныйFMN, т.к.DMN>FMN, то МF^/- внутренний луч углаDМN. А т.к. СD//АВ, тоMF^/NB, но симметрия - это биекцияи МFВА. Противоречие.

Опр. 2.Каждый из острых углов, образованных прямыми // прямой а, с перпендикуляром опущенными из их общей точки называется углом параллельности в т. М относительно прямой а.

Утверждение 2.Мера угла параллельности вполне определяется расстоянием от точки М до прямой а (не зависит от выбора т. М и прямой а).

Доказательство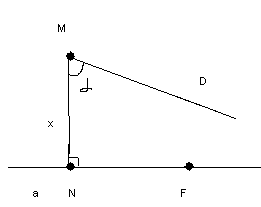

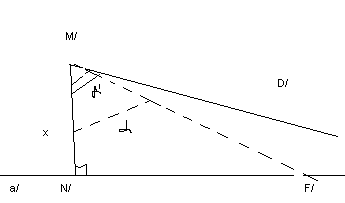
Пусть NMD-угол параллельности в т. М относительноа.N^/M^/D^/угол параллельности в т. М^/относительноа^/. Докажем, что еслиx=x^/, то^/ =.

Пусть ^/>.лучh^/-внутренний для углаN^/M^/D^/и такой, чтоN^/M^/F^/=, гдеh^/a^/=F^/. Нааот т.Nотложим т.F, так чтобыFиDлежали в одной полуплоскости иNF=N^/F^/, но тогдаNF=N^/F^/МNF=М^/N^/F^/NМF=MFи МDсовпадают, а значит МDиапересекаются. Противоречие. Ч.т.д.

Значит, мера угла параллельности есть функцияот х:

Обозначается =(х)- она называется функцией Лобачевского. Ясно, что (из Тh2)(х) определена для любого х0 и, кроме того, 0(х),k- некоторое положительное число.

(х)- монотонно убывающая функция и непрерывная, а значит, принимает все значения из (0,). Это означает, что любой острый угол является углом параллельности в некоторой точке относительно данной прямой.

Существование такой функций говорит о том, что между угловыми и линейными величинами имеется зависимость, т.е. - за единицу длины можно выбрать отрезок, которому соответствует угол параллельности, равный, например, .

§3. Треугольники и четырехугольники на плоскости Лобачевского

В этом § будут изложены некоторые факты, отличные от тех которые мы имеем в Евклидовой геометрии (сказать, что высоты не обязательно в одной точке).

Теорема 1.Сумма углов любого треугольника меньше 2d (т.е. меньше двух прямых).

Доказательство.ПоTh1 Саккери - Лежандра_АВС2d, но если она =2d, то имеет местоVпостулат по Тh2 (противоречие) ч.т.д.

Следствие.Сумма углов треугольника непостоянна.

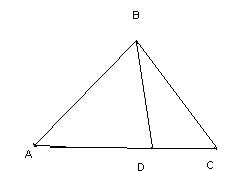
Пусть АВС - произвольный треугольник. Dстороне АС._АВС=_АВД+_BCD - 2d=АДС_ABC<_ABD.

Следствие 2.Сумма углов выпуклого четырехугольника меньше 4d.(очевидно).

Теорема 2. (четвертый признак равенства треугольников)Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны.

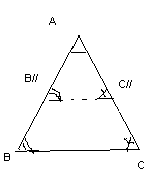
Доказательство:Пусть вАВС иА^/В^/С^/А=А^/,В=В^/,С=С^/. Достаточно доказать, что АВ=А^/В^/, а затем применитьпризнак равенства треугольников. Пусть АВА^/В^/, например, АВА^/В^/. На лучах АВ и АС возьмем т. В^//и С^//, так чтобы АВ^//=А^/В^/, АС^//=А^/С^/.АВ^//С^/=А^/В^/С^/В^//=В^/=В,С^//=С^/=С. В^//лежит между А и В. Надо доказать, что С^//лежит между А и С, ноВ=В^//прямая В^/С^//не пересекает ВСпо аксиоме Паша она пересекает АС, т.е. А-С^//-С. Четырехугольник В^//С^//СВ лежит по одну сторону от каждой прямой, содержащей его сторонуон выпуклый и его_В//С//СВ=4d, что противоречитследствию2 . Следовательно В^//совпадает с В.

Опр. 1 Двупрямоугольником называется выпуклый четырехугольник, у которого два угла, прилежащие к одной стороне, прямые.

П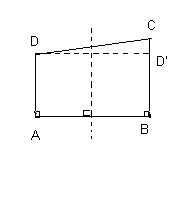устьABCD– двупрямоугольник.А иВ прямые. Тогда сторона АВ называетсяоснованием, аADиBC–боковыми сторонами.

Опр. 2 Двупрямоугольник с равными боковыми сторонами называется четырехугольником Саккери.

Свойство 1. Если АВСDчетырехугольник Саккери с основанием АВ, тоС=Dи оба они острые.

Доказательство. Рассмотрим симметрию с осьюd. При этомS_d(АD)=BС (BD^/=BC)D=С2d.

Свойства 2. Если в двупрямоугольнике с основанием АВ, АD<ВС, тоС<D. Легко.

Свойство 3. Если в двупрямоугольнике с основанием АВ,С<D, то АD<ВС. Самостоятельно.