§5. Окружность, эквидистанта и орицикл

Эти три типа линий связаны с тремя типами пучков прямых.

1⁰ Окружность.

Как известно окружность это множество точек равноудаленных от данной фиксированной точки. Это понятие абсолютной геометрии, а потому имеет место и в г. Л. и значит, многие свойства окружности переносятся в геометрию Лобачевского (но не все). Нам потребуется утверждение: любая прямая, лежащая в плоскости окружности, пересекается с ней не боле чем в двух точках.

Рассмотрим пучок пересекающихся прямых с центром в центре окружности. Каждая из прямых пучка называются осью окружности. Можно доказать свойства.

Свойство 1. Окружность симметрична относительно любой своей оси.

Свойство 2. В каждой точке окружностикасательная, котораяк оси, проходящей через точку касания.

Таким образом, окружность пересекает свои оси под прямым углом. Т.е. окружность есть ортогональная траектория пучка пересекающихся прямых .

Опр. 1.Пусть а, в - прямые. Аа и В в. Прямая АВ называется секущей равного наклона, если отрезки АВ составляет с этими прямыми равные внутренние односторонние углы.

С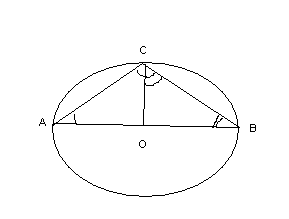войство 3.Прямая, содержащая хорду окружности, отличную от диаметра, является секущей равного наклона к осям, проходящим через концы хорды (очевидно).

Свойство 4.Серединный перпендикуляр к любой хорде окружности является ее осью (очевидно).

Не все теоремы об окружности справедливы на плоскости Лобачевского. Например, вписанный в окружность угол, опирающийся на диаметр, не является прямым: _АВС=2АСВ2dACBd

С пучком расходящихся прямых связана другая линия.

2⁰ Эквидистанта.

Опр. 1 Эквидистантой называется фигура, которая состоит из всех точек полуплоскости с границей u, равноудаленных от прямой u. Прямая u называется базой эквидистанты, а перпендикуляр, проведенный из любой точки эквидистанты на базу, высотой. Высотой будем называть так же длину этого . Осями эквидистанты называются прямые пучка расходящихся прямых перпендикулярных к базе.

Т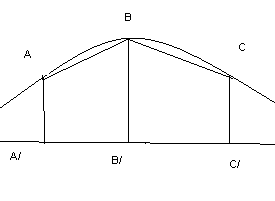еорема 1. Любая прямая лежащая в плоскости эквидистанты, пересекается с эквидистантой не более чем в двух точках.

Доказательство.От противного. Пусть точкиA,B,Cэквидистанты лежат на одной прямой.A^/,B^/,C^/- их проекции на базу. ТогдаABB^/A^/иB^/BCC^/- четырехугольники Саккери. Значит, углыABB^/иB^/BCострые. Противоречие.

Свойства:

1. Эквидистанта симметрична относительно любой своей оси.

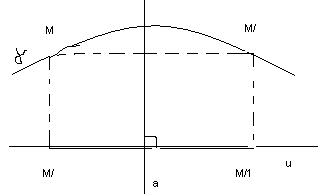
Доказательство.Пусть М– произвольная. Пусть М₁симметрично М относительноа. М^/и М^/₁ проекции точек М и М₁наu. М^/и М^/₁- симметричны относительноа. Поэтому ММ^/= М₁М^/₁ М₁.

2. В каждой точке эквидистанты  касательная, которая  к оси, проведенной через точку касания.

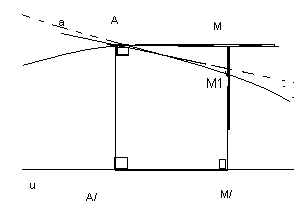
Доказательство. Пусть А,а АА₁аиu- расходятся, т.к. имеют общий, но расстояние от любой точки прямойадоuбольше (по Тh3 §4), чем АА^/. Значит, А - единственная точка эквидистанты, принадлежащая прямойа. Пусть Ма. М₁М^/ = АА^/если М₁А, то ММ^/АА^/М₁М0. И, значит, угол А^/АМ₁А^/АМсекущая имеет предельное положение – прямуюа. Значита- касательная. Ч.т.д.

Т.е. эквидистанта это ортогональная траектория пучка расходящихся прямых.

Хордой эквидистанты назовем любой отрезок, соединяющий две точки эквидистанты.

Свойство 3.Любая прямая, содержащая хорду эквидистанты, является секущей ровного наклона к осям, проходящим через концы хорды. (Очевидно).

Свойство 4. Серединныйк любой хорде эквидистанты является ее осью (очевидно, применяя осевую симметрию и свойство 3)

3⁰ Орицикл.

Эта линия связана с пучком // прямых.

ЛЕММА:Через каждую точку одной из двух параллельных прямых проходит единственная секущая ровного наклона к этим прямым(доказательство на практике).

Пусть на плоскости задан пучок // прямых. На множестве всех точек плоскости введем бинарное отношение: АВ если А совпадает с В или АВ - секущая ровного наклона к прямым пучка. Онорефлексивноисимметрично. Можно доказать, что оно транзитивно.

Опр. 3Каждый элемент фактор-множества / называется орициклом (предельной линией). Прямые пучка называютсяосямиорицикла.

В силу свойств классов эквивалентности, если задан пучок // прямых, то через каждую т. А плоскости проходит единственный орицикл. Это множество состоит из т. А и всех таких точек Х, что АХ – секущая ровного наклона к прямым пучка, проходящим через А и Х.

С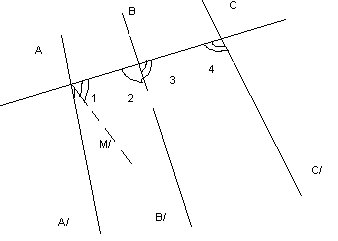другой стороны, ясно, что если задана направленная прямаяUVи т. А, то однозначно определяется орицикл, проходящий через А с осьюUV. Свойства орицикла анологичны свойствам окружности и эквидистанты. Так же как и окружность и эквидистанта, орицикл не является прямой линией. Об этом гласит следующая теорема:

Теорема 2.Любая прямая, лежащая в плоскости орицикла, пересекается с орициклом не более чем в двух точках

Доказательство (от противного). ПустьA,B,C– лежат на одной прямой. АА^/, ВВ^/, СС^/- оси. Они // и, т.к. это направленные прямые, то А^/, В^/и С^/лежат в одной полуплоскости. Прямая АВС – секущая равного наклона. Т.к. // прямые не имеют общего, то углы 1, 2, 3, 4-не прямые. Д-жем, что они острые. Пусть2- тупой, сл-но3 - острый,1-тупой. ОтложимВАМ^/=3. Т.к. АА^///ВВ^/ АМ^/пересекает ВВ^/. это противоречие, т.к.3=ВАМ и они соответственные,2 и3 острые и не могут быть смежными. Ч.т.д.

Имеют место свойства 1⁰-4⁰окружности и эквидистанты.

Орицикл есть ортогональная траектория пучка параллельных прямых.

Итак: Окружность, эквидистанта и орицикл это линии с очень похожими свойствами.